22. Одноместным предикатом р(X) называется произвольная функция переменного X, определенная на множестве m и принимающая значение из множества {1; 0}.
Множество М, на котором определен предикат Р(x), называется областью определения предиката Р(x).
Множество всех
элементов
,
при которых предикат принимает значения
“истина” (1), называется множеством
(областью) истинности предиката Р(x),
т.е. множество истинности предиката
Р(х)- это множество
или иначе:
или так:
Так, например, предикат Р(x) – “x – простое
число” определен на множестве N, а
множество истинности IP
для него есть множество всех простых
чисел.
Предикат Q(x) –
“sinx=0” определен на множестве R, а его
множеством истинности является
Предикат F(x) – “диагонали параллелограма x взаимно перпендикулярны” определен на множестве всех параллелограмов, а его множеством истинности является множество всех ромбов.
Из приведенных примеров видим, что одноместные предикаты выражают свойства предметов (субъектов).
23. При применении квантора общности к предикату р(х) с полем м
(навешивании квантора на предикат), получаем высказывание “для
любого х из поля М Р(х)”. Это высказывание обозначается:
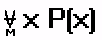
и истинно тогда, когда при подстановке любого значения из поля М
предикат Р(х) становится истинным высказыванием и ложно тогда,
когда при подстановке хотя бы одного из значений в Р(х) получается
ложное высказывание.
Если поле обозначения предиката ясно из содержания, то
можно использовать тоже обозначение
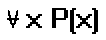
Это высказывание можно прочитать и так: “для всех х
справедливо Р(х)”, “для каждого х Р(х)”.
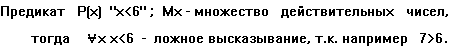
При навешивании на предикат Р(х) с полем М квантора
существования получается высказывание: “существует такое
значение х, что Р(х)”. Это высказывание обозначается:
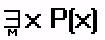
Или
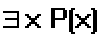
и истинно тогда, когда М имеется хотя бы одно значение переменной
х, при подстановке которого в Р(х) получается истинное
высказывание.
Если таких переменных нет, то высказывание
является ложным. Оно является истинным высказыванием, если в
соответствующей строке матрицы предиката Р(х) имеется хотя бы
одно значение “И”. Если же строка состоит только из “Л”, то
высказывание ложно.
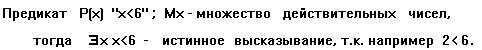
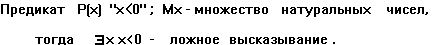
24. Двухместным предикатом Р(x,y) называется функция двух переменных x и y, определенная на множестве М=М1хМ 2 и принимающая значения из множества {1;0}.
В числе примеров двухместных предикатов можно назвать такие предикаты: Q(x, y) – “x=y” - предикат равенства, определенный на множестве RхR=R2; F(x,y) – “х параллелен y”, “прямая х параллельна прямой y”, определенный на множестве прямых, лежащих на данной плоскости.
25. В двухместных предикатах Р(x,y) выделяются две переменные, у
которых есть свои поля Мх и Мy.
Пример: Р(x,y) -“x>y” ; Mx={2;4}, My={0;1;3}. Матрица предиката
имеет вид:
x y |
0 |
1 |
3 |
2 |
И |
И |
Л |
4 |
И |
И |
И |
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36. Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
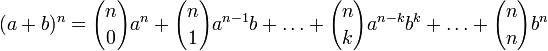
Где
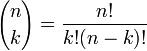
37.
38. Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятностей и обладает занимательными свойствами.
39. Граф — это совокупность непустого множества вершин и множества пар вершин.
Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами.
Наглядным представлением графа является диаграмма, на которой вершины графа изображаются произвольно расположенными на плоскости точками. Ребра изображаются линиями, которые соединяют между собой точки, соответствующие смежным вершинам.
Матрица инциденций — таблица, которая содержит набор строк и столбцов. Каждая строка соответствует узлу, а каждый столбец — ветви графа. Если ветвь с номером направлена от узла то в i-ой строке и j-ом столбце записываем +1. Если i-ая ветвь направлена к узлу, то в i-ой строке и j-ом столбце записываем -1. Все остальные элементы матрицы инциденций равны нулю.
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.
Матрица достижимости простого ориентированого графа G = (V,E) — бинарная матрица замыкания по транзитивности отношения E (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.