Упражнение 8.

а) Докажите, что геометрическим местом точек плоскости (множеством точек плоскости), равноудалённых от двух данных точек, является прямая, проходящая через середину отрезка, соединяющего эти точки и перпендикулярная ему. Она так и называется – серединным перпендикуляром.

б) Выведите отсюда, что через любые три точки плоскости, не лежащие на одной прямой, можно провести, причём единственным образом, окружность.

Def. Окружность, проходящая через все три вершины треугольника называется его описанной окружностью. Окружность, касающаяся всех трёх сторон треугольника, называется его вписанной окружностью. Угол, вершина которого находится в центре окружности, называется центральным. Угол, вершина которого находится на самой окружности, называется вписанным (в эту окружность).

Упражнение 9.

Центральный угол равен удвоенному описанному углу, опирающемуся на ту же дугу окружности. Рассмотрите все три возможные случая:

Выведите, в качестве следствия, что угол, опирающийся на диаметр – прямой.

D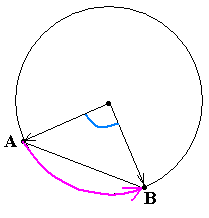 ef. Две точки А и В на окружности делят её на две дуги. Если не указан порядок, то под дугой АВ мы понимаем меньшую из этих двух дуг, а если порядок важен, то ту из них, которая получается при обходе от первой указанной точки ко второй при движении против часовой стрелки. Отрезок, соединяющий эти две точки, называется хордой. Если выбран какой-то эталон угла, например, прямой угол, то можно, сравнивая с ним остальные углы, ввести меру угла, говорить о величине угла. Дуги измеряются этой же мерой: под угловой величиной дуги понимается величина центрального угла, опирающегося на неё.

Упражнение 10.

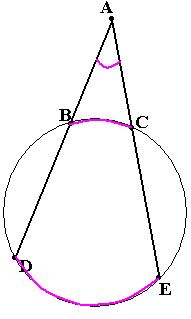
1. П усть точка А находится вне окружности и две секущие, пересекающиеся в точке А, пересекают окружность в точках В и С и ещё раз в точка D и Е. Докажите, что угол А равен полуразности дуг DE и BC.

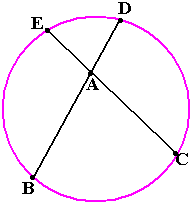
2. Пусть точка А находится внутри окружности и две хорды, пересекающиеся в точке А, пересекают окружность в точках В и С и ещё раз в точка D и Е. Докажите, что угол САВ равен полусумме дуг DE и BC.

Упражнение 11.

а )Докажите, что геометрическим местом точек плоскости (ГМТ), равноудалённых от двух пересекающихся прямых, является пара прямых -биссектрис образованных ими вертикальных у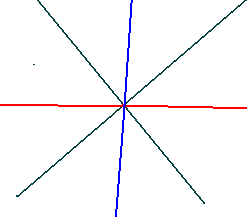 глов. б) докажите, что эти две биссектрисы всегда взаимно перпендикулярны.

Упражнение 12.*

Докажите, что прямая, перпендикулярная радиусу и инцидентная его концу, является касательной к окружности. Обратно, касательная к окружности перпендикулярна радиусу, проведённому к точке касания.

Упражнение 13.

Докажите, что у любого треугольника существует, и при том единственная, вписанная в него окружность.

Упражнение 14.

1. Докажите, что если диагонали некоторого четырехугольника делятся их точкой пересечения пополам, то этот четырехугольник – параллелограмм;

2. Докажите, что если у некоторого четырехугольника имеется пара сторон, которые конгруэнтны и параллельны, то этот четырехугольник – параллелограмм.

Def.

Отрезок, соединяющий середины сторон треугольника, называется его средней линией.

Упражнение 15*. (теорема о средней линии треугольника)

1. С редняя линия треугольника параллельна его третьей стороне и вдвое меньше её.

2. если в треугольнике отрезок, соединяющий две его стороны, параллелен третьей его стороне и вдвое меньше её, то он – средняя линия в этом треугольнике.

3. если прямая делит одну сторону треугольника пополам и параллельна второй его стороне, то третью сторону треугольника она тоже делит пополам.

Упражнение 16. (Теорема Вариньона)

Пусть АВСD – произвольный четырехугольник, возможно даже невыпуклый. Пусть M, N, K и L – середины сторон АВ, ВС, CD и DE соответственно. Тогда четырехугольник MNKL - параллелограмм.

Упражнение 17.

М едианы в треугольнике делятся точкой их пересечения в отношении 2:1, считая от вершин. В частности, все три медианы пересекаются в одной точке.

(Hint: look)

Упражнение 18.

Отрезки касательных к окружности, проведённые из одной точки, конгруэнтны.

Упражнение 19.

Найдите сумму углов выпуклого n-угольника.

Это можно сделать двумя способами: поставив точку внутри этого многоугольника и триангулировав его, либо рассмотреть сумму внешних углов этого многоугольника, откладывая их от одной из его вершин.

Упражнение 20. (признак вписанности для четырехугольника)

Для того, чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы сумма его противоположных углов была конгруэнтна развёрнутому углу.

Def. В прямоугольном треугольнике сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны называются катетами.

Упражнение 21.

1. Докажите, что в прямоугольном треугольнике гипотенуза больше любого из катетов;

2. докажите, что в любом треугольнике сумма любых двух сторон больше третьей, а разность любых двух сторон меньше третьей;

3. Докажите, что длина любой ломаной АВ…С больше отрезка АС, соединяющего начало и конец ломаной.

4. медиана треугольника меньше полусуммы сторон, выходящих из той же вершины.

Упражнение 22. (признак описанности для четырехугольника)

Для того, чтобы в четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы суммы его противоположных сторон были равны.

Упражнение 23.

П роведём через вершины треугольника прямые, параллельные его сторонам. Докажите, что у получившегося треугольника углы конгруэнтны углам исходного треугольника, а стороны в два раза больше.

Мы уже знаем с вами, что биссектрисы треугольника пересекаются в одной точке – центре его вписанной окружности. Докажем теперь,

Упражнение 24*.

Высоты треугольника пересекаются в одной точке, называемой его ортоцентром¹.

(combine ##8 & 22)

В классических задачах на построение, дошедших до нас из глубины веков, из Древней Греции, присутствуют два инструмента: бесконечная односторонняя линейка без делений и циркуль. С помощью линейки можно провести прямую линию через две данные точки. С помощью циркуля можно провести окружность с центром в данной точке и радиусом, равным расстоянию до другой данной точки. В некоторых задачах можно пользоваться другими инструментами: двусторонней линейкой с параллельными краями, уголком (прямым углом), имеющимся шаблоном – треугольником, например и т.д. Особняком стоят задачи «оригами», когда можно перегибать нарисованную на листе бумаги фигуру. Если не оговорено особо, будем считать, что слова «построить» означают «построить циркулем и линейкой».

Упражнение 25.

1. Разделить данный отрезок пополам;

2. Провести биссектрису заданного угла.

Упражнение 26.

1. Из точки, не инцидентной данной прямой, опустить на неё перпендикуляр.

2. Из точки, инцидентной данной прямой, восстановить к ней перпендикуляр.

3. Через точку, не инцидентную данной прямой, провести параллельную ей линию.

Упражнение 27.

Дана окружность. Построить её центр.

Упражнение 28*.

Из точки вне данной окружности провести к ней касательную.

Упражнение 29*.

Дана окружность и её диаметр.

П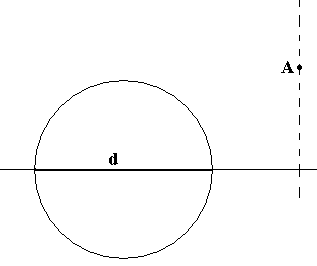 ользуясь только линейкой, опустить из данной точки, не инцидентной прямой, содержащей этот диаметр и не лежащей на окружности, перпендикуляр на эту прямую.

Рассмотрите все возможные случаи расположения точки: вне окружности над диаметром, над его продолжением (как на рисунке слева) и внутри окружности.

Упражнение 30.

Д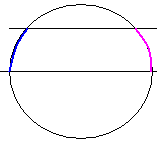 окажите, что параллельные прямые высекают на окружности равные дуги.

Def. Четырехугольник, две стороны которого параллельны, а две другие – не параллельны, называется трапецией. Параллельные стороны называются основаниями трапеции, а пара других сторон – её боковыми сторонами. Если боковые стороны равны, то такая трапеция называется равнобочной.

Упражнение 31.

Трапеция равнобочна  углы при основании этой трапеции равны.

Упражнение 32.

Средняя линия трапеции (соединяет середины боковых сторон) равна полусумме её оснований и параллельна им.

Упражнение 33.

1. Докажите, что трансверсаль в треугольнике всегда меньше одной из двух, выходящих из той же вершины, сторон.

2. Докажите, что сумма расстояний от точки, лежащей на стороне треугольника, до его вершин меньше суммы длин этой стороны и одной из двух других сторон треугольника.

3. Докажите, что сумма расстояний от любой точки внутри треугольника до его вершин меньше периметра треугольника, но больше его полупериметра.

Упражнение 34.

Циркулем и линейкой:

1. Восстановить из данной точки  к данной прямой.

2. Отложить от данного луча в данной полуплоскости угол, равный данному углу.

Упражнение 35*.

И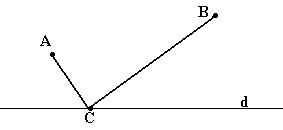 меется дорога d и две деревни – А и В. Где на дороге следует установить остановку автобуса С так, чтобы сумма расстояний (АС + СВ) от неё до двух деревень была минимальной?

Упражнение 36*.

Д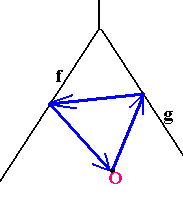 ве железнодорожные ветки f и g расходятся под острым углом, а между ними находится будка путевого обходчика. Обходчику нужно выйти из своей будки в точке О, побывать на обоих путях и вернуться обратно. Каким образом он должен выбрать маршрут, чтобы его путь (периметр синего треугольника) был наименьшим?

Упражнение 37.

Центры и точка касания двух окружностей лежат на одной прямой.

У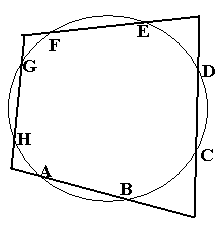 пражнение 38.

Окружность пересекает все стороны четырехугольника в двух точках. Все образовавшиеся хорды равны между собой. Докажите, что в этот четырехугольник можно вписать окружность.

Упражнение 39.

1. Придумайте квартиру в виде многоугольника с прямыми углами такого, чтобы в нём можно было поместить лампу так, чтобы ни одна стена этой квартиры не была освещена полностью.

2. Тот же вопрос, но лампа помещается снаружи.

Упражнение 40.

Для АВС и А₁В₁С₁ выполняются равенства: АВ=А₁В₁; АС=А₁С₁ и АВС=А₁В₁С₁. Докажите, что либо эти треугольники равны, либо С+С₁=.

Упражнение 41.

Верно ли, что четырехугольник является параллелограммом, если две его стороны равны, а две другие параллельны?

Упражнение 42.

Пусть a, b – катеты прямоугольного треугольника, c – его гипотенуза. Докажите, что диаметр окружности, вписанной в этот треугольник, равен a+b-c.

Упражнение 43.

Диагонали выпуклого четырехугольника ABCD пересекаются в О. Известно, что АО=ОС и АВ‖CD. Можно ли утверждать, что ABCD – параллелограмм?

Упражнение 44.

Докажите, что если в треугольнике совпадают центры вписанной и описанной окружностей, то этот треугольник правильный

Упражнение 45.

Через точку М внутри окружности проведены три хорды. М является серединой двух хорд. В каком отношении делит она третью хорду?

Упражнение 46.

Нарисуйте такой шестиугольник, который Яков Иосифович не сможет разрезать на два четырехугольника.

Упражнение 47.

Предложите удобный, практичный способ измерения диагонали кирпича, который вы достали из груды одинаковых кирпичей, лежащих во дворе.

Упражнение 48.

Предложите удобный, практичный способ измерения радиуса футбольного мяча.

Упражнение 49.

1. Как измерить объём булыжника? (Remember Physics)

2. Как измерить толщину листа бумаги?

Упражнение 50.

Докажите, что сумма диагоналей четырехугольника меньше его периметра, но больше его полупериметра.

«Построить» означает построить с помощью циркуля и линейки.

Упражнение 51.

Построить треугольник по заданной стороне и высотам, проведённым к другим сторонам.

Упражнение 52.

Построить прямоугольный треугольник по гипотенузе и проведённой к ней высоте (из вершины прямого угла).

Упражнение 53.*

Построить прямоугольный треугольник по острому углу при гипотенузе и сумме катетов.

У пражнение 54.

ABCF и FCDE – квадраты.K – середина BC, CL=¼CE, M– середина DE. Докажите, что точки K,L и M лежат на одной прямой и что Kl=LM.

Упражнение 55.

A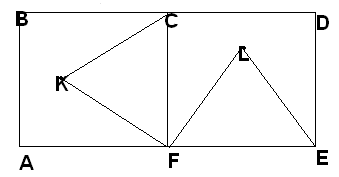 BCF и FCDE – квадраты, CKF и FEL – правильные треугольники. Докажите, что точки K, L и D лежат на одной прямой.

Упражнение 56.

В окружность вписаны две равнобедренные трапеции с соответственно параллельными сторонами. Докажите, что диагональ одной из них равна диагонали другой трапеции.   

Упражнение 57.

На плоскости нарисована окружность. С помощью чертёжного угольника найдите её центр.

Упражнение 58. На сторонах произвольного четырёхугольника как на диаметрах построены круги. Доказать, что они покрывают его целиком.

Упражнение 59.

А и В – два города. Найти ГМТ таких, что если из них идти напрямик в В, то расстояние до А будет всё время увеличиваться. Следствия из №16:

1. Середины сторон четырёхугольника являются вершинами прямоугольника Û диагонали этого четырёхугольника перпендикулярны.

2. Середины сторон четырёхугольника являются вершинами ромба Û диагонали этого четырёхугольника равны.

3. Середины сторон равнобочной трапеции являются вершинами ромба.

Упражнение 60.

Дан угол, вершина которого недоступна и точка а) внутри него, б) вне него. Построить прямую, проходящую через эту точку и недоступную вершину.

Упражнение 61.

Можно ли расположить на плоскости 2011 прямых так, чтобы каждая из них пересекалась ровно с 2004 прямыми?

Упражнение 62. Дан параллелограмм ABCD с острым углом при вершине A. На лучах AB и CB отмечены точки H и K соответственно, причём CH = BC и AK = AB. Докажите, что DH =DК.

Упражнение 63*.

На сторонах АВ, ВС и АС треугольника АВС выбраны произвольным образом точки С₁, А₁ и В₁ соответственно. Около треугольников СА₁В₁, ВА₁С₁ и АВ₁С₁ описаны окружности. Докажите, что у всех трех окружностей имеется общая точка.

Упражнение 64.

В данную окружность впишите прямоугольный треугольник, катеты которого проходили бы через две данные точки внутри окружности. При каких условиях это возможно?

В каком случае решение будет единственным?

Упражнение 65.

На дуге BC окружности, описанной около равностороннего треугольника ABC, взята произвольная точка P. Докажите, что AP = BP + CP.

Упражнение 66.

В параллелограмме АВСD опустили перпендикуляр DН на сторону АВ. Точки Е и F – середины сторон BC и AD соответственно. Докажите, что BF=EH.

Упражнение 67.

В треугольнике АВС отметили произвольную точку D на медиане ВМ. Провели через С прямую, параллельную ВМ, а через D - прямую, параллельную АВ. Эти прямые пересеклись в точке Е. Докажите, что ВЕ=АD.

Упражнение 68.

В прямоугоьном треугольнике АВС из вершины прямого угла С опущена высота СD на гипотенузу АВ. На отрезке АD отмечена точка Е такая, что СD=DE и из точки Е восстановлен перпендикуляр к гипотенузе АВ до пересечения в точке F с катетом АС. Найдите величину угла СВF.

Упражнение 69.

Вершина A треугольника ABC соединена отрезком с центром O описанной окружности. Из вершины A проведена высота AH. Докажите, что BAH = OAC.   

Упражнение 70.

Две окружности пересекаются в точках A и B. Продолжения хорд AC и BD первой окружности пересекают вторую окружность в точках E и F. Докажите, что прямые CD и EF параллельны.   

Упражнение 71.

Точки A, B, C и D лежат на окружности. Точки M, N, K и L — середины дуг AB, BC, CD и DA, последовательно расположенных на окружности. Докажите, что хорды MK и NL перпендикулярны.   

Упражнение 72.

Пусть O — центр окружности, описанной около треугольника ABC , AOC = 60^o . Найдите угол AMC , где M — центр окружности, вписанной в треугольник ABC .

Упражнение 73.

Продолжения биссектрис остроугольного треугольника ABC пересекают описанную окружность в точках A₁, B₁ и C₁ соответственно. Докажите, что высоты треугольника A₁B₁C₁ лежат на прямых AA₁, BB₁ и CC₁.  

Упражнение 74.

Продолжения высот остроугольного треугольника ABC пересекают описанную окружность в точках A₁, B₁ и C₁ соответственно. Докажите, что биссектрисы треугольника A₁B₁C₁ лежат на прямых AA₁, BB₁, CC₁.

Упражнение 75.

В окружность вписан четырёхугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке E. Прямая, проходящая через точку E и перпендикулярная к AB, пересекает сторону CD в точке M.

Докажите, что EM — медиана треугольника CED.

Упражнение 76.

На гипотенузе AС прямоугольного треугольника ABC во внешнюю сторону построен квадрат с центром в точке O. Докажите, что ВО — биссектриса прямого угла.

Упражнение 77.

На окружности даны точки A, B, C, D в указанном порядке; M — середина дуги AB. Обозначим точки пересечения хорд MC и MD с хордой AB через E и K. Докажите, что KECD — вписанный четырёхугольник.

Упражнение 78*.

Отрезки AB и CD — диаметры одной окружности. По окружности скользит точка М. Из неё опускают перпендикуляры MP и MQ на прямые AB и CD. Докажите, что длина отрезка PQ является инвариантом положения точки М (не зависит от положения точки M).

Упражнение 79.

В треугольнике ABC угол B равен 60^o, биссектрисы AD и CE пересекаются в точке O. Докажите, что OD = OE.   

Упражнение 80.

На окружности, описанной около остроугольного треугольника ABC, лежит центр другой окружности, проходящей через вершины A, C и точку пересечения высот треугольника ABC. Найдите угол АВС.

Упражнение 81*.

Докажите, что отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной окружностью пополам.  

Упражнение 82.

В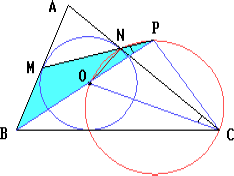 писанная окружность касается сторон AB и AC треугольника ABC в точках M и N. Пусть P — точка пересечения прямой MN и биссектрисы угла B (или её продолжения). Докажите, что BPC = 90^o. (Hint: look at the picture).

Упражнение 83.

AM — биссектриса треугольника ABC. Точка D принадлежит стороне AC, причём DMC = BAC. Докажите, что BM = MD.

Упражнение 84*.

На сторонах AC и BC треугольника ABC во внешнюю сторону построены квадраты ACA₁A₂ и BCB₁B₂. Докажите, что прямые A₁B, A₂B₂ и AB₁ пересекаются в одной точке.

(Hint: Prove, that it is the point of intersection of two circumferences, circumscribed around squares).

Упражнение 85.

Четырёхугольник ABCD, диагонали которого взаимно перпендикулярны, вписан в окружность. Перпендикуляры, опущенные на сторону AD из вершин B и C, пересекают диагонали AC и BD в точках E и F соответственно. Найдите EF, если BC = 1.

Упражнение 86.

На сторонах произвольного треугольника ABC во внешнюю сторону построены равносторонние треугольники ABC₁, A₁BC и AB₁C. Докажите, что прямые AA₁, BB₁ и CC₁ пересекаются в одной точке. (Hint: remember #84)

Упражнение 87*. (прямая Симсона.)

Докажите, что основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), лежат на одной прямой.

Упражнение 88*.

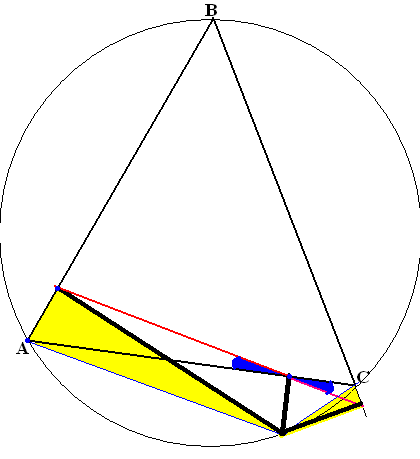
В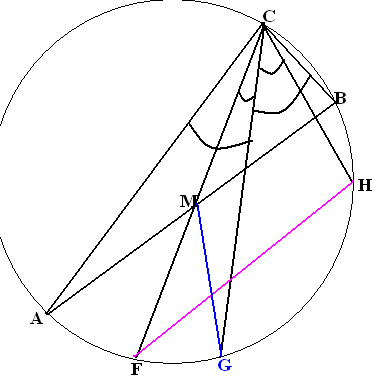 треугольнике ABC стороны AC и BC не равны. Докажите, что биссектриса угла C делит пополам угол между медианой и высотой, проведёнными из вершины C, тогда и только тогда, когда C = 90^o.

(Hint: look at the picture).

Упражнение 89*.

С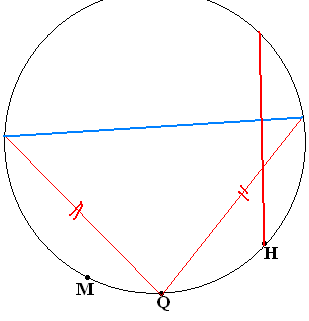 помощью циркуля и линейки постройте треугольник по точкам пересечения с его описанной окружностью высоты, медианы и биссектрисы, проведённых из одной вершины.

(Hint: look at the picture).

Упражнение 90*.

Окружности S₁ и S₂ пересекаются в точке A. Через точку A проведена прямая, пересекающая S₁ в точке B, S₂ — в точке C.

В точках C и B проведены касательные к окружностям, пересекающиеся в точке D. Докажите, что угол BDC не зависит от выбора прямой, проходящей через точку A.

У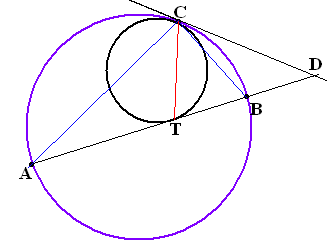 пражнение 91*.

Две окружности касаются внутренним образом в точке C. Пусть AB — хорда большей окружности, касающаяся меньшей окружности в точке T. Докажите, что CT — биссектриса угла ACB.

Упражнение 92.

В параллелограмме ABCD диагональ AC больше диагонали BD. Точка M на диагонали AC такова, что около четырёхугольника BCDM можно описать окружность. Докажите, что BD — общая касательная окружностей, описанных около треугольников ABM и ADM.

Упражнение 93*.

Во вписанном четырёхугольнике ABCD через вершины A, B и точку P пересечения диагоналей проведена окружность, пересекающая сторону BC в точке E. Дано: AB = AD. Докажите, что CD = CE.

Упражнение 94*.

На сторонах АВС вне его построены квадраты ВСDЕ и СFGA. Докажите, что центры квадратов и середины АВ и DF являются вершинами квадрата.

Упражнение 95.

Две окружности пересекаются в точках A и B. Через точку B проводится прямая, пересекающая вторично окружности в точках C и D, а затем через точки C и D проводятся касательные к этим окружностям. Докажите, что точки A, C, D и точка P пересечения касательных лежат на одной окружности.   

Упражнение 96.

Постройте трапецию по

1. Основаниям и боковым сторонам;

2. По основаниям и диагоналям.

Упражнение 97. (Теорема Фалеса)

П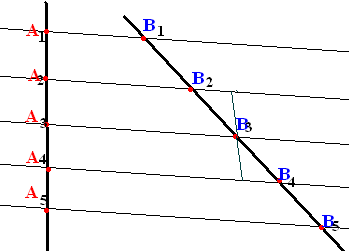 усть параллельные прямые отсекают на прямой c равные отрезки. Тогда на любой другой прямой, которую они пересекут, они также отсекут равные отрезки.

Упражнение 98. Разделите данный отрезок на 7 равных частей.

Упражнение 99. (Теорема о пропорциональных отрезках). (для соизмеримых отрезков)

П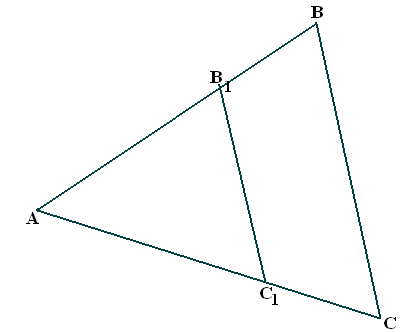 усть на стороне АС треугольника ВАС выбрана точка С₁ так, что отрезки АС и АС₁ соизмеримы (т.е., найдётся некоторый отрезок, который укладывается целое число раз и на отрезке АС и на отрезке АС₁). Пусть, далее, через точку С₁ проведена прямая параллельная ВС, которая пересекает сторону АС в точке В₁. Тогда .

Соизмеримость отрезков означает, что отношение длин этих отрезков является рациональным числом (почему?).

Упражнение 100.

Даны (соизмеримые) отрезки a, b и c. Построить отрезок х такой, что a:b=c:x.

Упражнение 101.

Пусть имеется гомотетия с центром О и коэффициентом kQ.

1. Д окажите, что при этом расстояния между любыми двумя точками плоскости увеличивается (при k<1 уменьшается, а при k<0 ещё происходит и отражение относительно О) в k раз.

2. Докажите, что при этом прямые, не проходящие через центр гомотетии переходят в параллельные им прямые (а прямые, проходящие через этот центр, – сами в себя).

3. Докажите, что образы трёх точек, инцидентных одной прямой, инцидентны одной прямой.

Д оказав это утверждение, используя чертёж и теорему №99 (дважды!), докажите то же самое другим способом, с помощью векторов. Сравните оба способа – который из них вам показался проще?

Это упражнение открывает перед нами новую группу преобразований плоскости: группу подобий. Она состоит из всех композиций преобразований, компонентами которых являются конгруэнции и гомотетии. Например, элементом этой группы будет последовательность abcdcega, где а – отражение относительно некоторой прямой, b – гомотетия относительно некоторой точки О₁ с коэффициентом k₁, c – поворот относительно некоторой точки О₂ на угол , d – параллельный перенос на вектор d, e - гомотетия относительно некоторой точки О₃ с коэффициентом k₂, g - поворот относительно некоторой точки О₄ на угол . Поскольку при каждом таком преобразовании прямые линии переходят в прямые линии, причём параллельные линии переходят в параллельные, и расстояния между любыми двумя точками изменяются с одним и тем же коэффициентом пропорциональности, это же верно и для их композиции.

Def. Фигуры, принадлежащие одной орбите при действии группы подобий, называются подобными.

В нашем изложении пока что коэффициенты гомотетий – рациональные числа.

Упражнение 102. (признаки подобия треугольников)

Докажите, что два треугольника подобны, если

1. У них имеется пара соответственно конгруэнтных углов, а стороны одного из них, инцидентные вершине этого угла пропорциональны сторонам другого треугольника, составляющим конгруэнтный ему угол с одним и тем же коэффициентом пропорциональности k;

2. У них имеется две пары соответственно конгруэнтных углов;

3. Стороны одного из них пропорциональны сторонам другого с одним и тем же коэффициентом пропорциональности k.

Упражнение 103.

П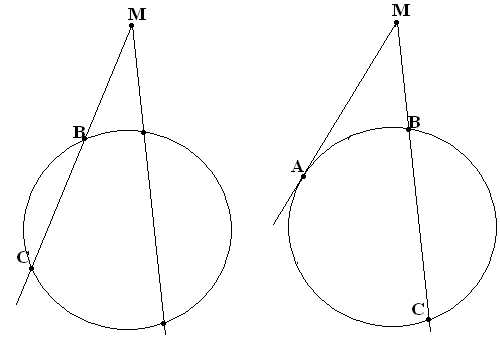 усть даны окружность S и точка М вне круга В, ограниченного этой окружностью. Пусть секущая, проведённая из точки М пересекает окружность S в точках В и С. Тогда произведение МВМС является инвариантом (то есть, не зависит от положения секущей. В частности, если имеется касательная МА, то МВМС=МА².

Упражнение 104.

П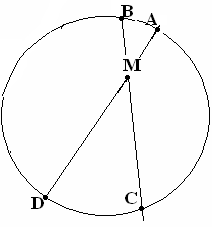 усть даны окружность S и точка М внутри неё. Проведём через М хорду, встречающую окружность S в точках В и С. Тогда величина МВМС является инвариантом (то есть, не зависит от проведения хорды, постоянна для любой хорды, проходящей через М).

На этих двух упражнениях основано множество задач, некоторые из которых предлагаются вам далее.

Упражнение 105.

Д окажите, что высота прямоугольного треугольника, опущенная из прямого угла, является средним геометрическим отрезков, на которые она делит его гипотенузу: BD²=ADDC.

Выведите отсюда способ построения (циркулем и линейкой) среднего геометрического двух отрезков.

Упражнение 106.

Докажите обратную по отношению к №103 теорему, дающую ещё один полезный критерий того, что четыре точки лежат на одной окружности:

Пусть на сторонах угла ВАС выбраны точки В₁ и С₁ так, что АВАВ₁=АСАС₁.

Тогда точки В, В₁, С и С₁ лежат на одной окружности.

Упражнение 107.

Д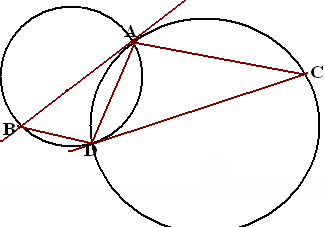 аны две окружности, пересекающиеся в точках A и D; AB и CD - касательные к первой и второй окружностям (B и C — точки на окружностях). Докажите, что . (Hint: use the theorem about angle between a chord and a tangent line)

Упражнение 108.

Д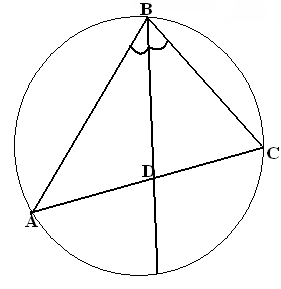 окажите, что биссектриса делит сторону треугольника в соотношении равном отношению прилегающих к ней сторон:

АВ:ВС=AD:DC. (Hint: circumscribe circumference around triangle ABC)

Упражнение 109*.

С помощью циркуля и линейки постройте окружность, проходящую через две данные точки и касающуюся данной прямой.    (Hint: use ##103, 105)

У пражнение 110**.

Через данную точку проведите окружность, касающуюся данной прямой и данной окружности. Рассмотрите разные варианты расположения прямой и окружности. Для одного из них на рисунке указаны в качестве подсказки дополнительные построения. В этом случае у задачи имеются 4 решения. Как обычно, начинать надо с анализа предполагаемого решения.

Упражнение 111*.

Н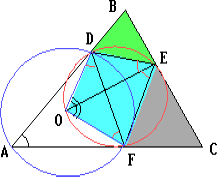 а сторонах AB, BC и AC треугольника ABC взяты соответственно точки D, E и F так, что DE = BE, FE = CE. Докажите, что центр описанной около треугольника ADF окружности лежит на биссектрисе угла DEF.

Подсказкой к решению служит прилагаемый слева чертёж.

Упражнение 112.

Н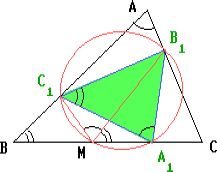 а сторонах AB, BC и CA треугольника ABC зеленой краской отметили соответственно точки C₁, A₁ и B₁, отличные от вершин треугольника. Оказалось, что , а BAC=B₁A₁C₁. Докажите, что треугольник с зелеными вершинами подобен треугольнику ABC.   

Упражнение 113.

Д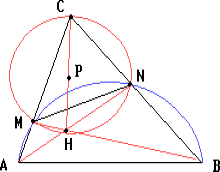 ля данной хорды MN окружности рассматриваются треугольники ABC, основаниями которых являются диаметры AB этой окружности, не пересекающие MN, а стороны AC и BC проходят через концы M и N хорды MN. Докажите, что высоты всех таких треугольников ABC, опущенные из вершины C на сторону AB, пересекаются в одной точке.

Упражнение 114.

Три окружности имеют общую точку M и попарно пересекаются в точках P, Q, R. Через произвольную точку A одной из окружностей, лежащую на дуге PQ, не содержащей точки M, и точки P и Q, в которых окружность пересекает две другие окружности, проведены прямые, пересекающие эти же две окружности в точках B и C. Докажите, что точки B, C и R лежат на одной прямой.