
Модуль 4.
Линейные отображения и операторы векторных пространств.
Ядро и образ линейного оператора.
Матрица линейного оператора.
Алгебра линейных операторов.
Обратимые линейные операторы.
Собственные векторы и значения линейного оператора.
Характеристический многочлен линейного оператора.
Спектр линейного оператора.
Условия подобия матрицы диагональной матрице.
План практических занятий Модуль 1.
ЗАНЯТИЯ 1, 2. Обратная матрица. Ранг матрицы.
Найти обратные матрицы по формуле или с помощью элементарных преобразований. а)
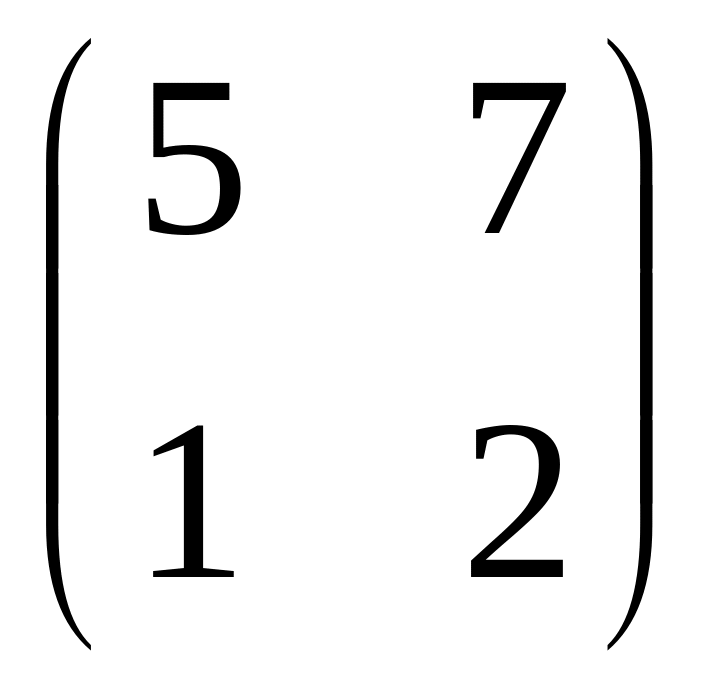 ;
б)
;
б)
 ;
в)
;
в)
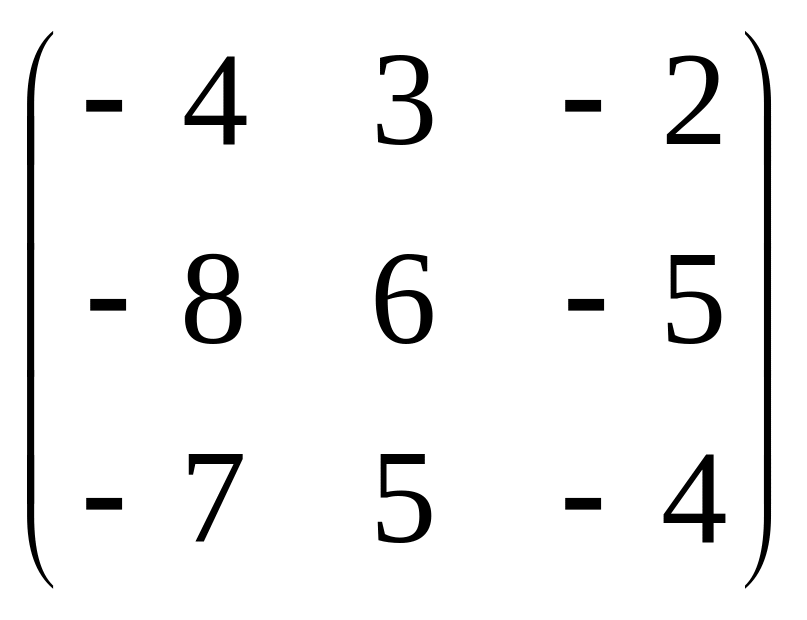 ;
г)
;
г)
 .
Ответ:
а)
.
Ответ:
а)
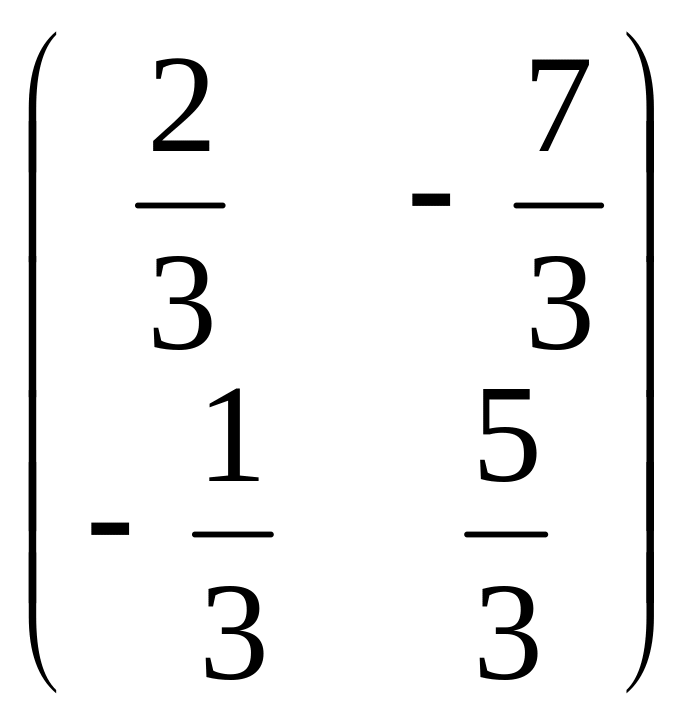 ;
б) не существует; в)
;
б) не существует; в)
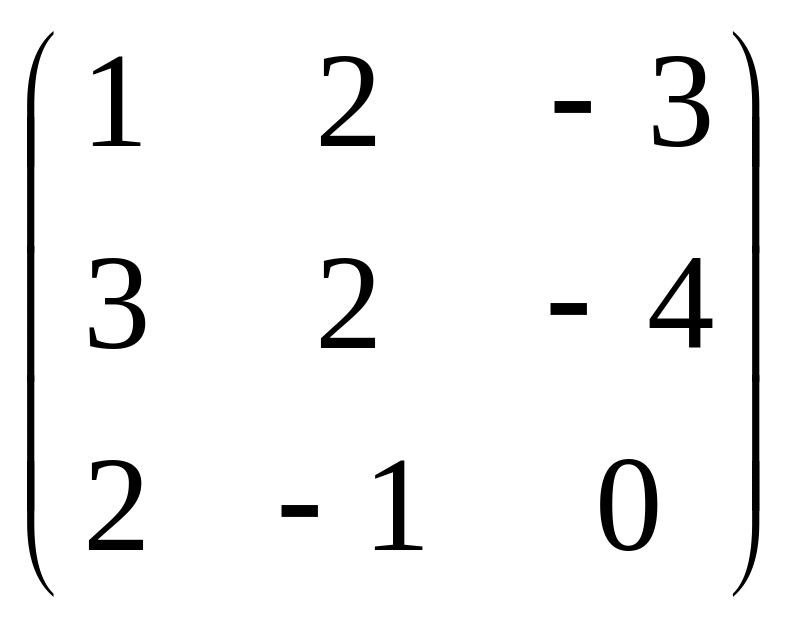 ;
г)
;
г)
 .
.Даны матрицы
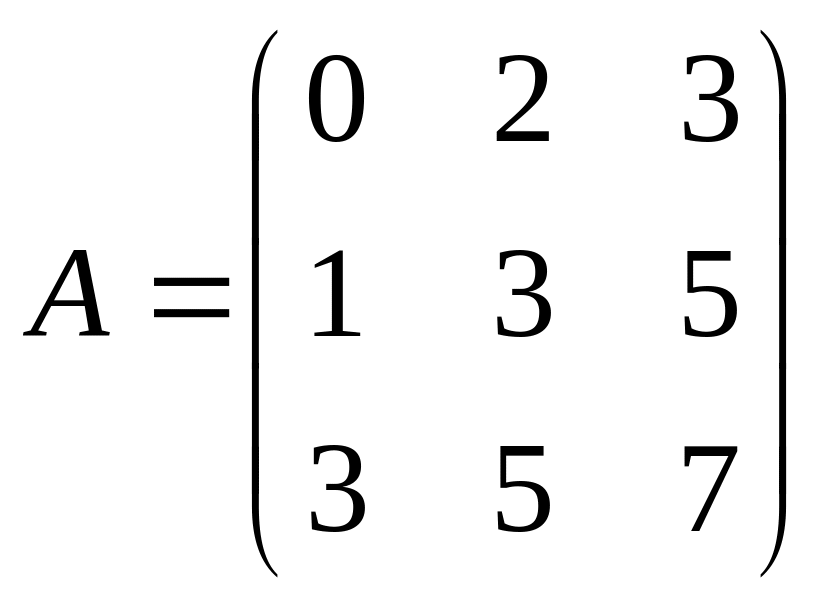 ,
,
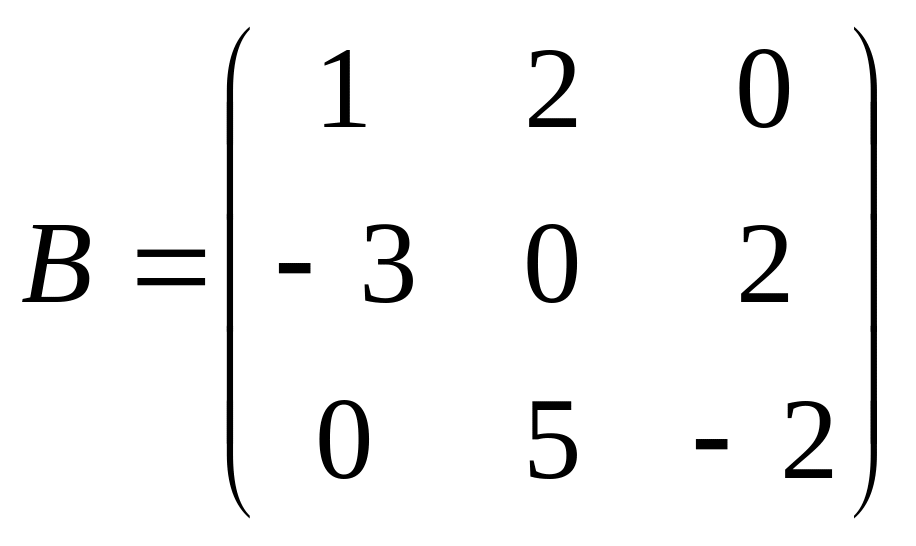 .
Решить матричные уравнения:
а) AX=B;
б) XA=B.
Ответ: а)
.
Решить матричные уравнения:
а) AX=B;
б) XA=B.
Ответ: а)
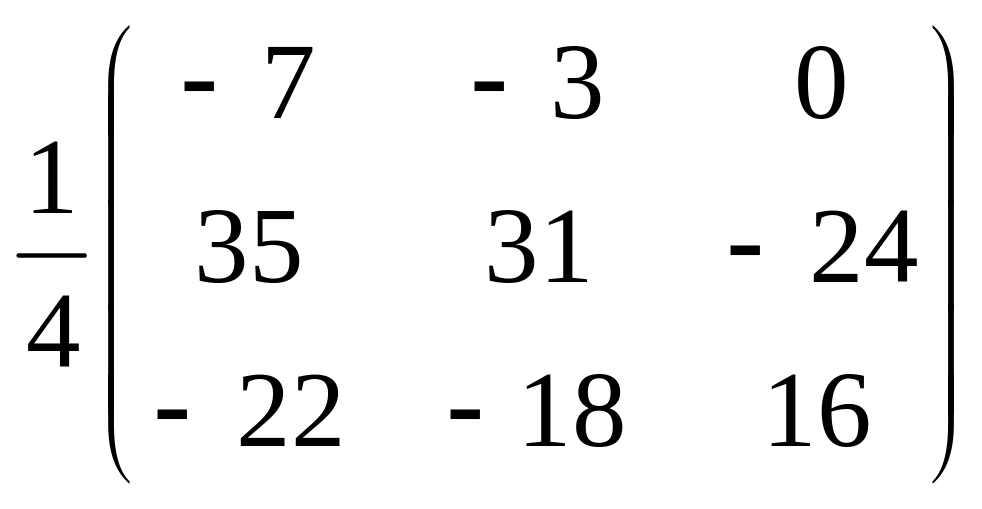 ;
б)
;
б)
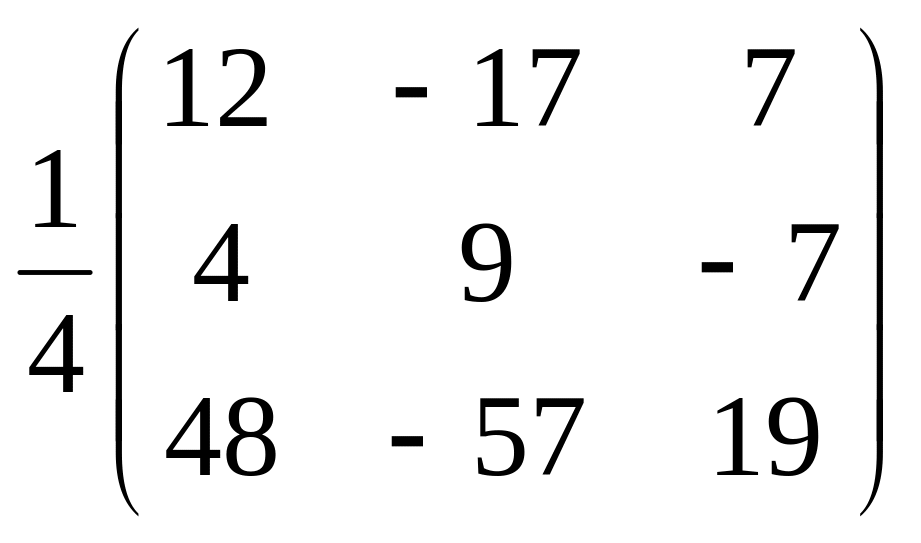 .
.Вычислить ранги матриц: а)
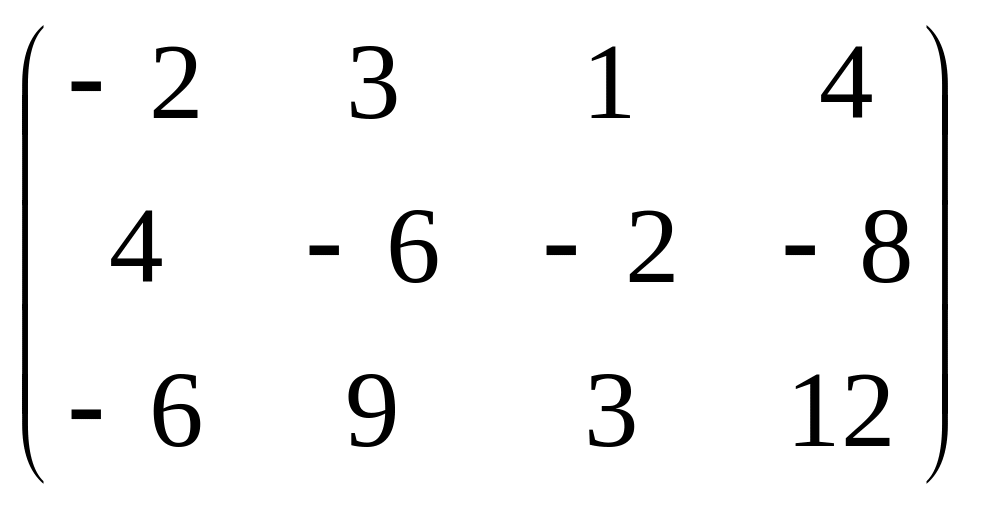 ;
б)
;
б)
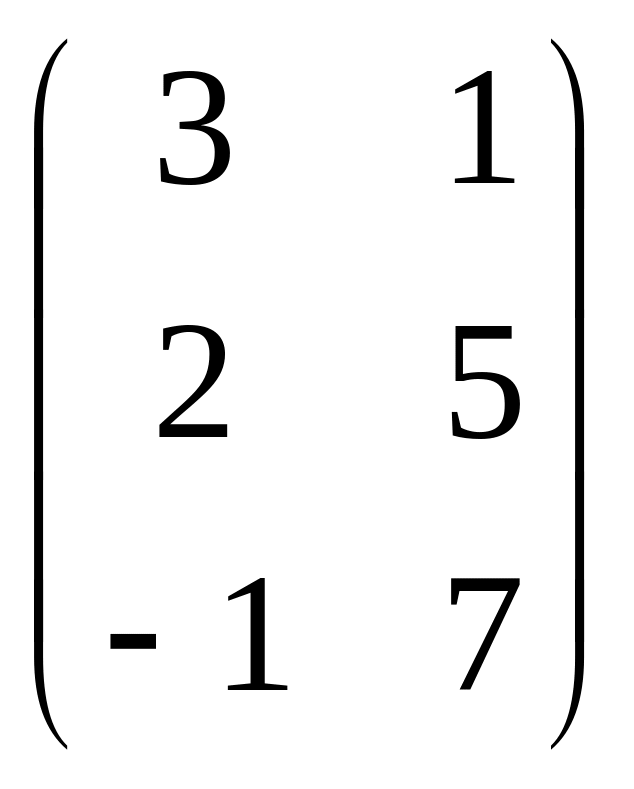 ;
в)
;
в)
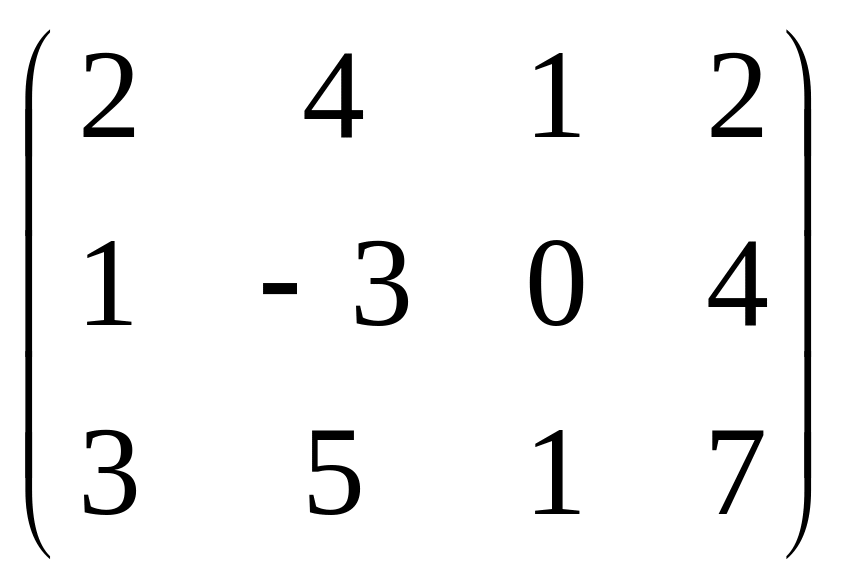 ;
г)
;
г)
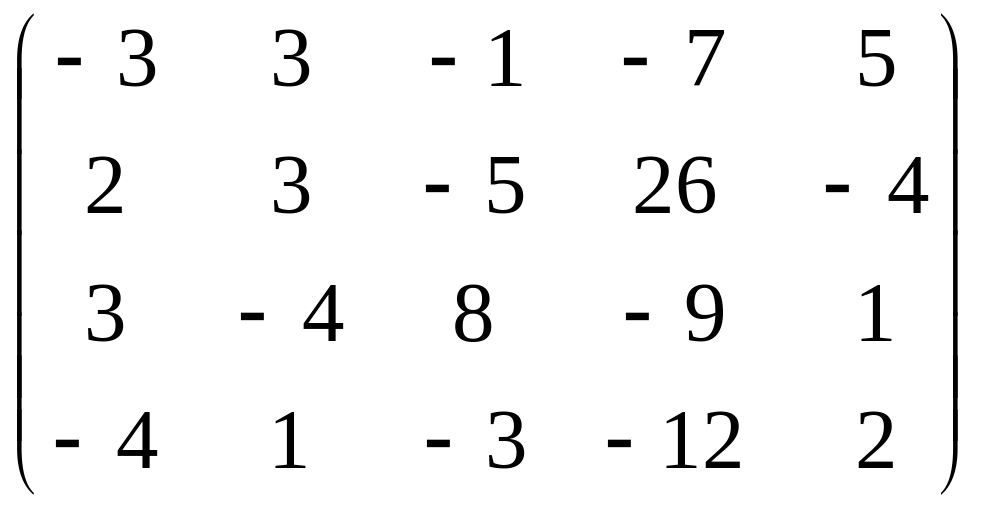 ;
д)
;
д)
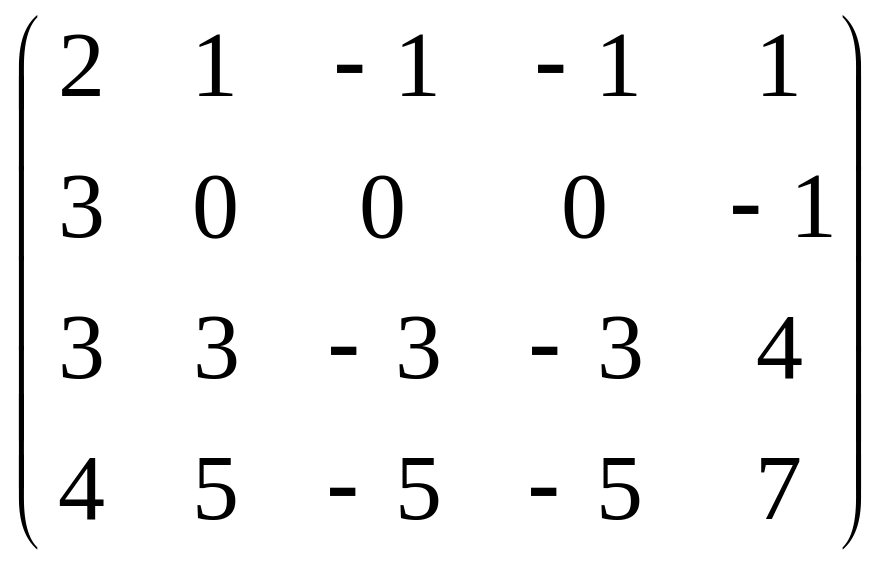 .
Ответ: а) 1; б) 2; в) 3; г) 3; д) 2.
.
Ответ: а) 1; б) 2; в) 3; г) 3; д) 2.
ЗАНЯТИЯ 3, 4. Системы линейных уравнений.
Решить системы линейных уравнений методом Крамера или матричным методом. а)
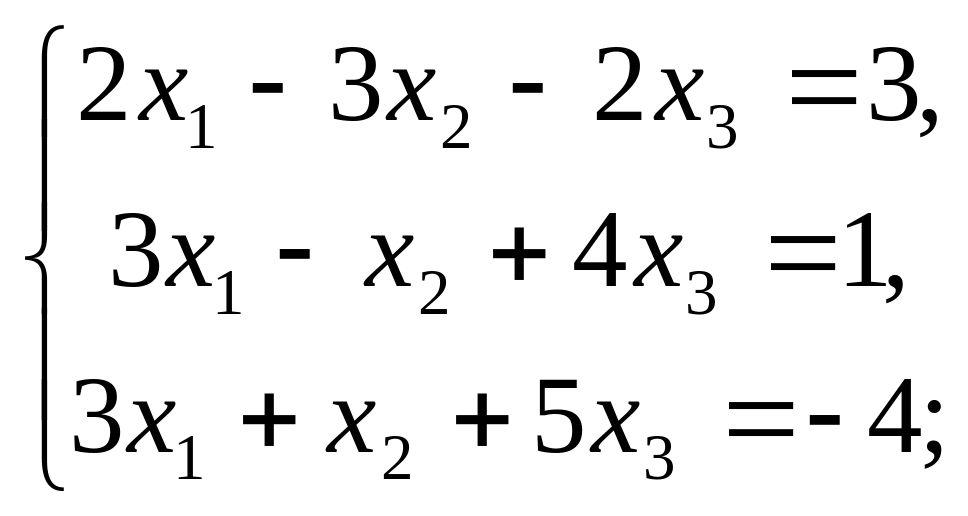 б)
б)
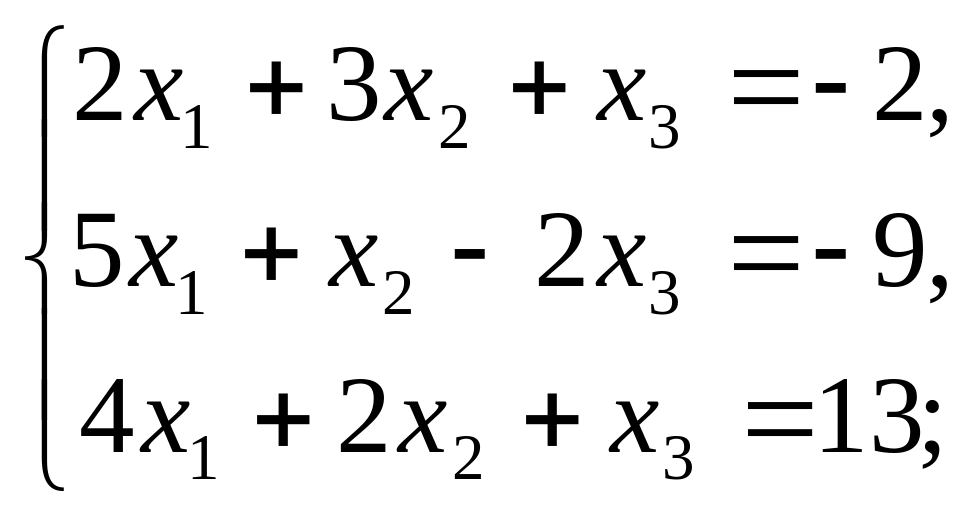 в)
в)
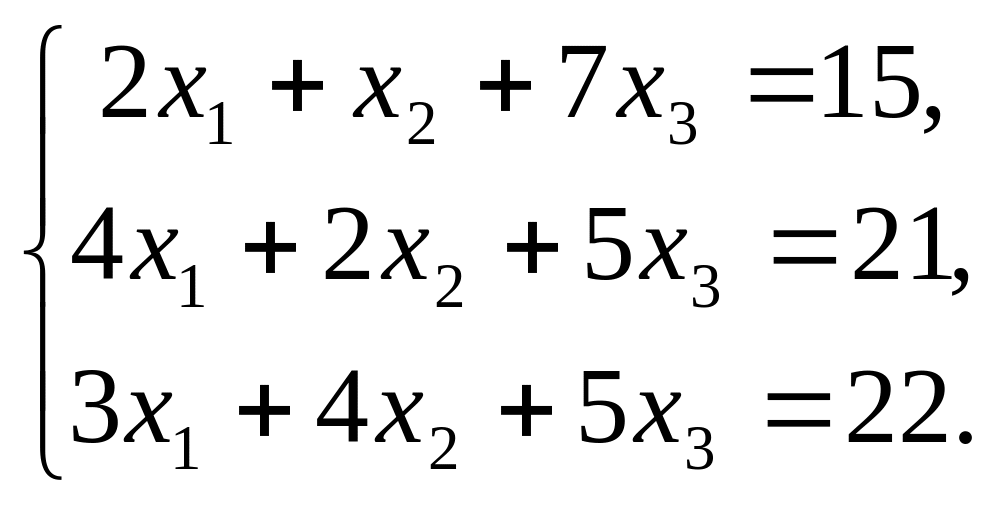 Ответ:
а)
Ответ:
а)
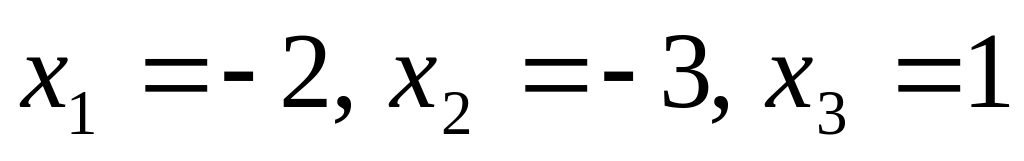 ;
б)
;
б)
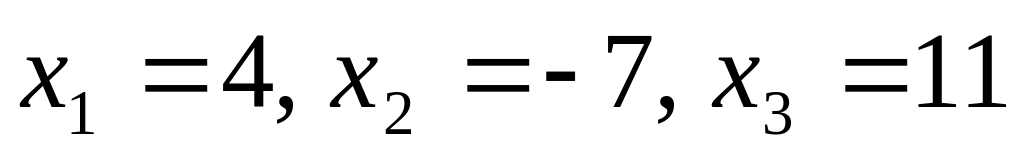 ;
в)
;
в)
 .
.Решить систем линейных уравнений методом Гаусса: а)
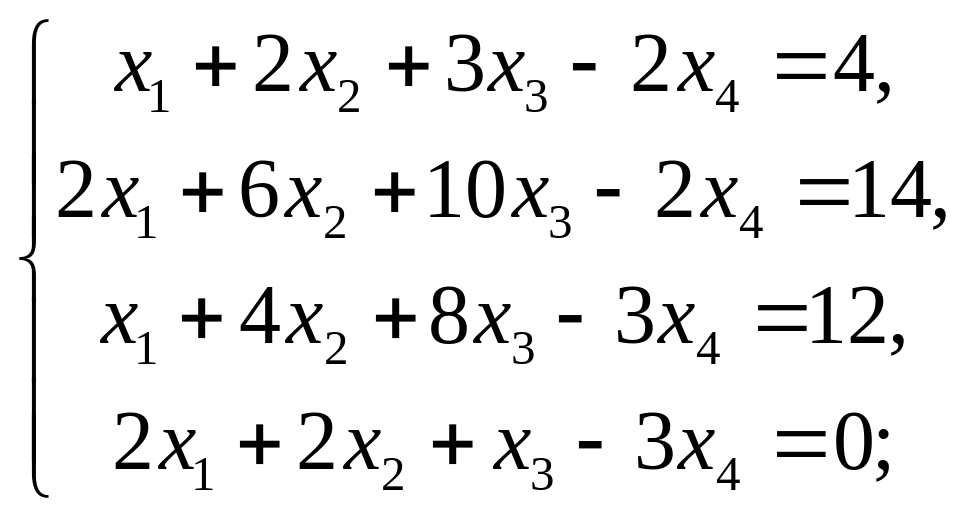 б)
б)
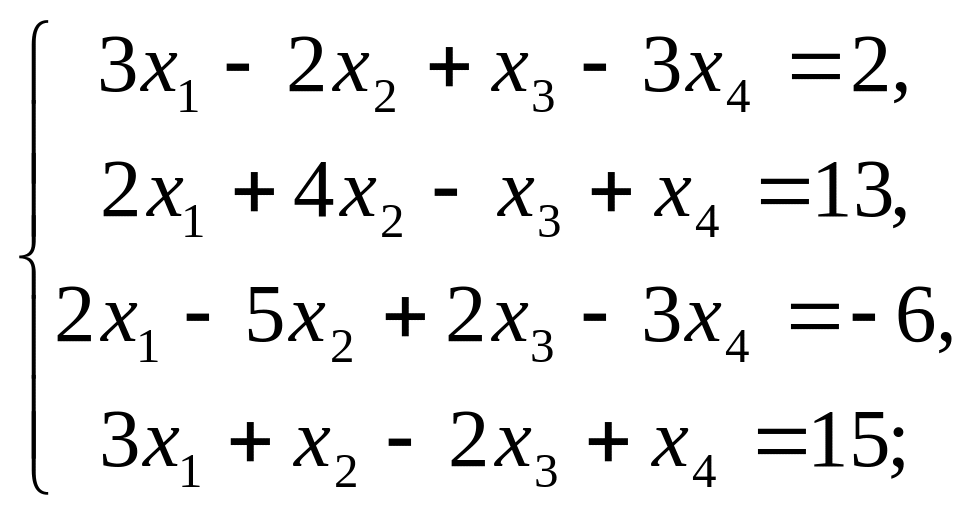 в)
в)
 г)
г)
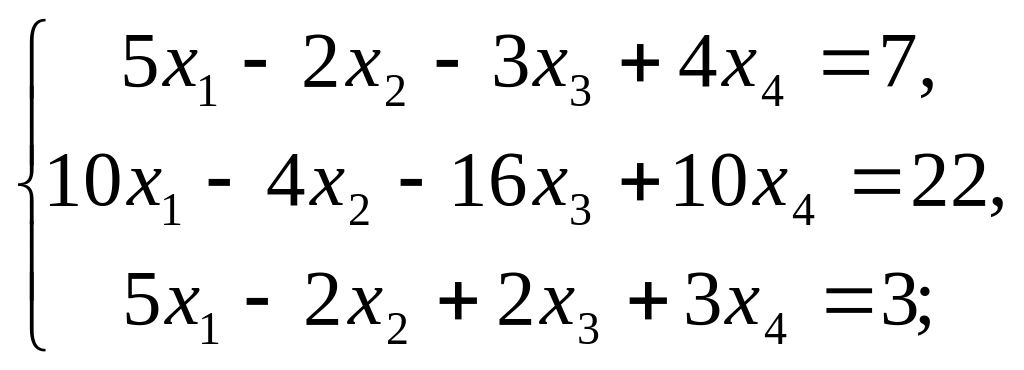 д)
д)
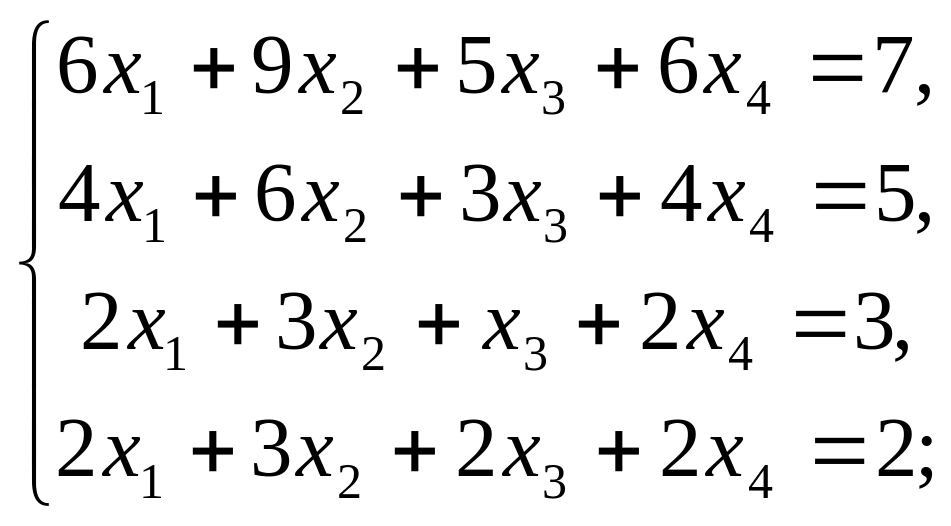 е)
е)
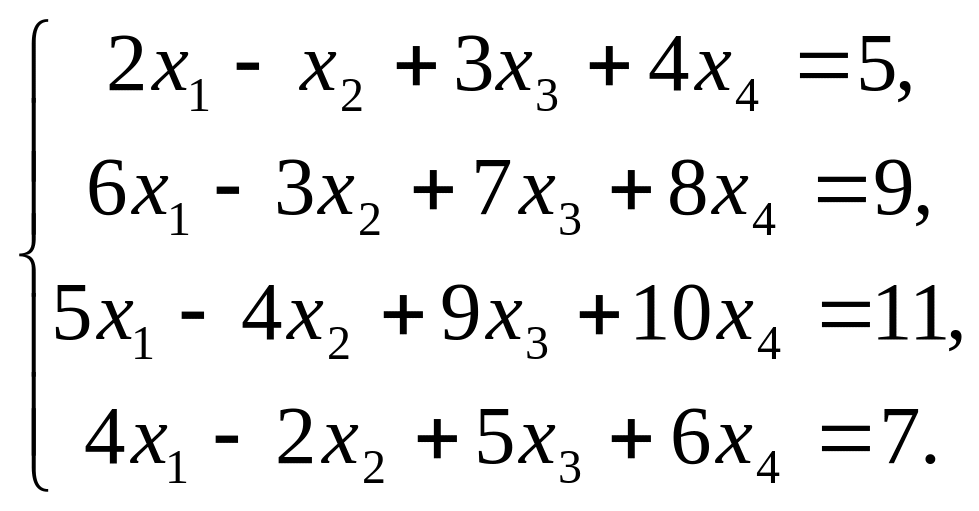 Ответ:
а)
Ответ:
а)
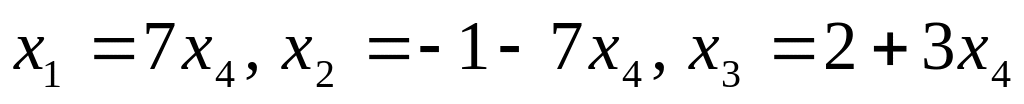 ;
б)
;
б)
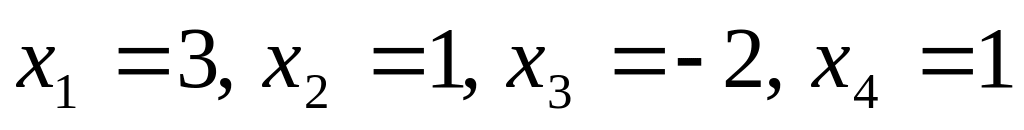 ;
в)
несовместна; г)
;
в)
несовместна; г)
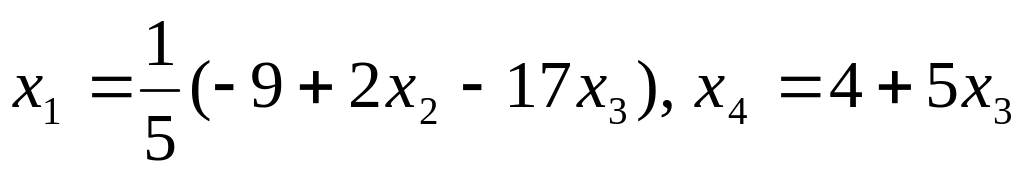 ;
д)
;
д)
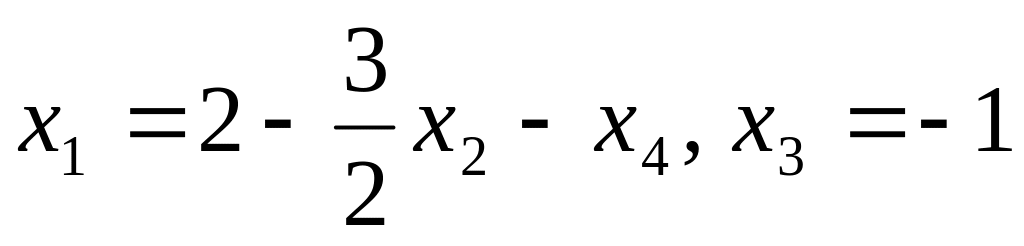 ;
е)
;
е)
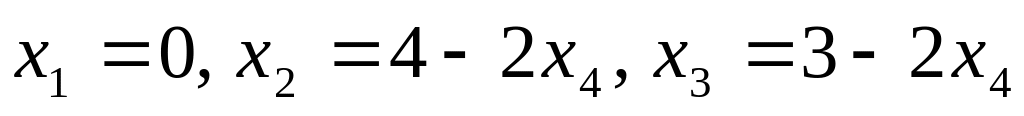 .
.Исследовать систему и решить ее в зависимости от значений параметра:
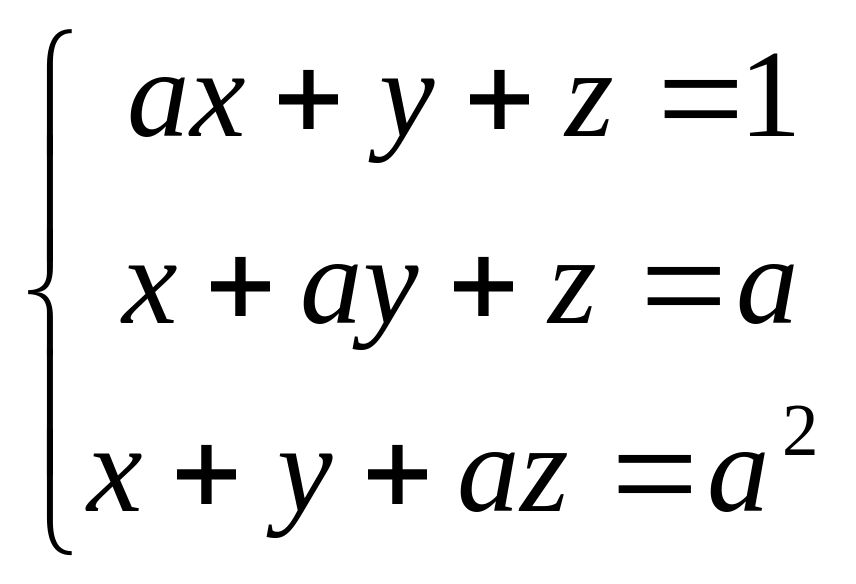 .
Ответ: при
.
Ответ: при
![]() система имеет единственное решение
система имеет единственное решение
![]() ;
при
;
при
![]() общее решение имеет вид
общее решение имеет вид
![]() ;
при
;
при
![]() система несовместна.
система несовместна.
Модуль 2.
ЗАНЯТИЕ 5, 6. Линейно зависимые и независимые системы векторов.
Установить линейную зависимость или независимость следующих систем векторов в соответствующих векторных пространствах над полем R:
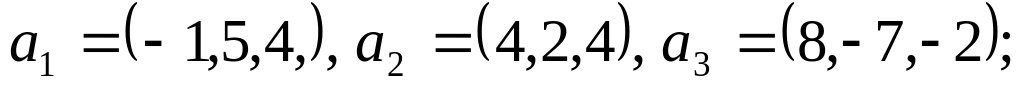 .
Ответ: система линейно зависима и
.
Ответ: система линейно зависима и
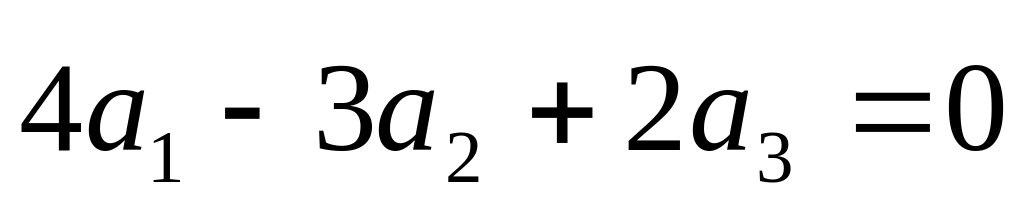 .
.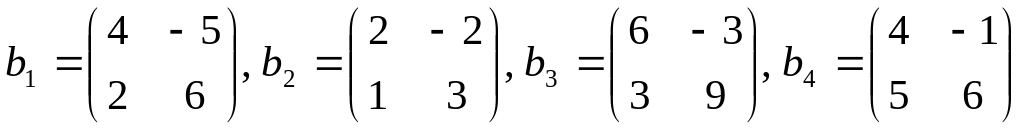 .
Ответ: система линейно зависима и
.
Ответ: система линейно зависима и
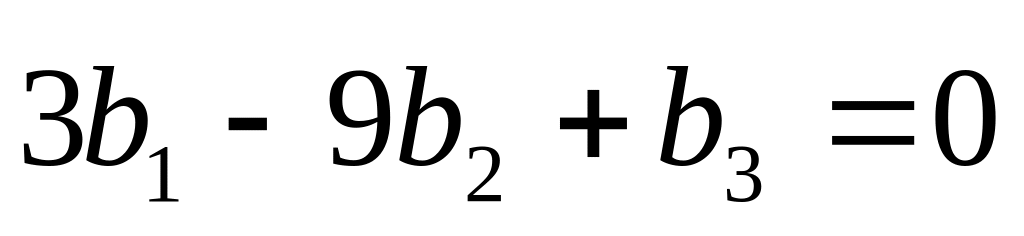 .
.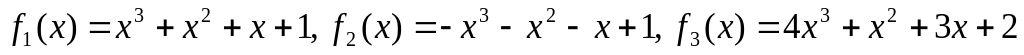 .
Ответ: система линейно независима.
.
Ответ: система линейно независима.
В векторном пространстве
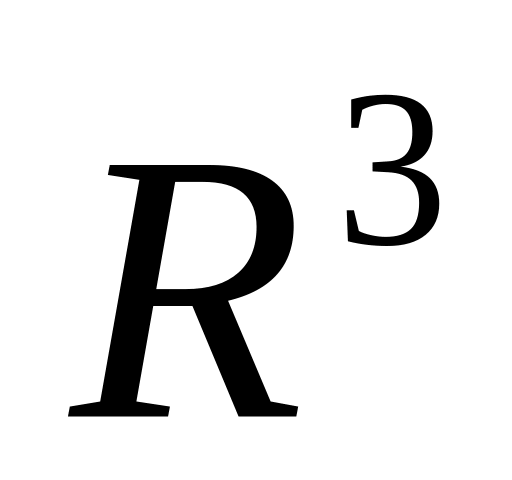 представить вектор a=(1,4,–7)
как линейную комбинацию векторов
представить вектор a=(1,4,–7)
как линейную комбинацию векторов
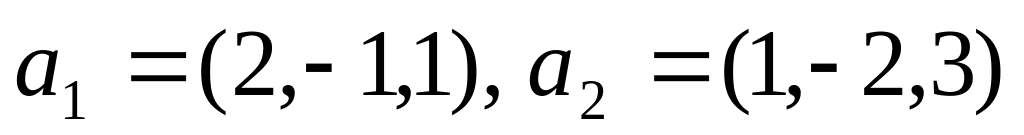 .
Ответ:
.
Ответ:
 .
.Доказать, что вектор a=2–7i из векторного пространства C над R линейно выражается через векторы
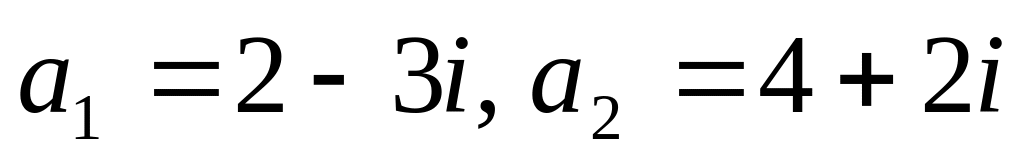 .
Ответ:
.
Ответ:
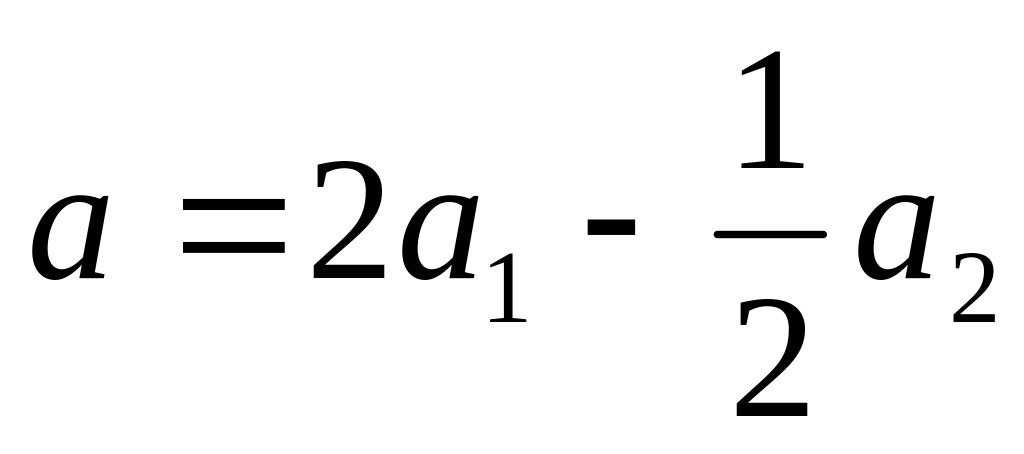 .
.
ЗАНЯТИЕ 7. Координаты вектора в базисе.
Данную линейно независимую систему дополнить до базиса соответствующего векторного пространства:
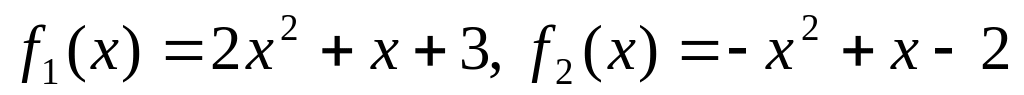 .
Ответ:
.
Ответ:
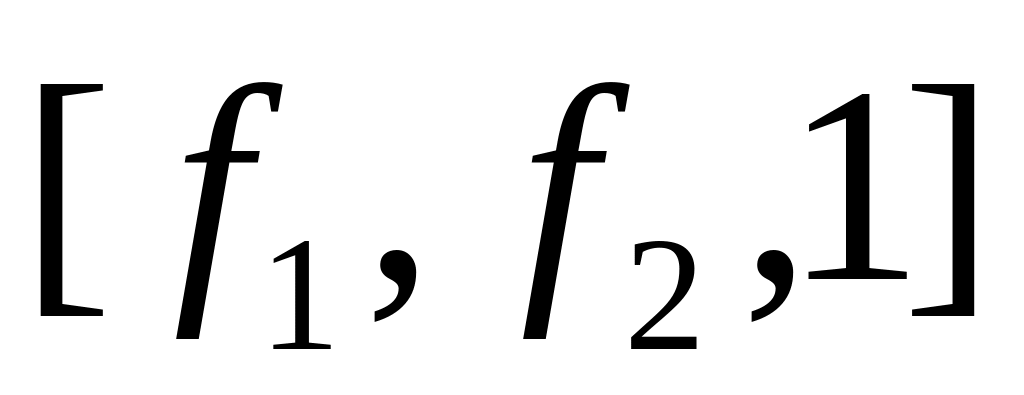 .
. .
Ответ:
.
Ответ:
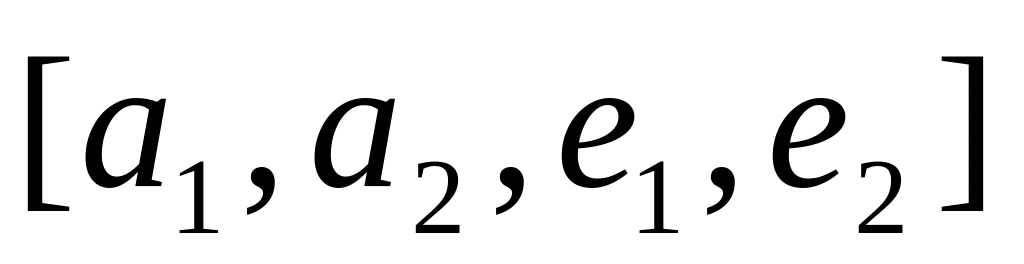 .
.
Доказать, что система
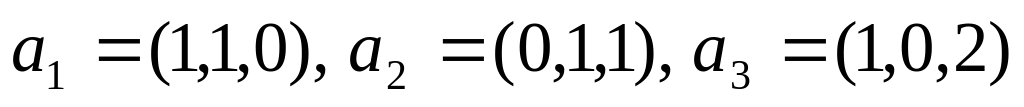 составляет базис пространства
.
Найти в этом базисе координаты вектора
a=(2, –3,
5). Ответ:
составляет базис пространства
.
Найти в этом базисе координаты вектора
a=(2, –3,
5). Ответ:
 .
.Найти координаты вектора
 из векторного пространства
из векторного пространства
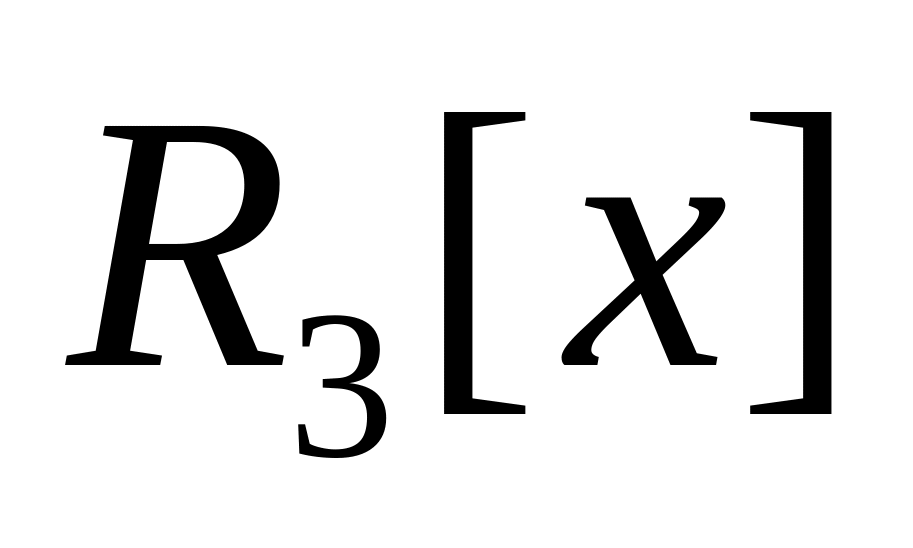 в базисах:
в базисах: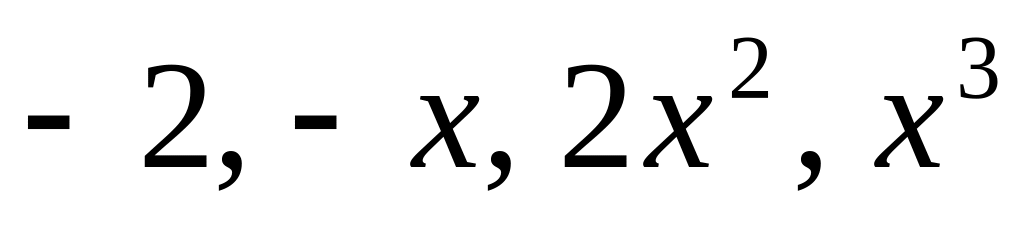 .
Ответ:
.
Ответ:
 .
.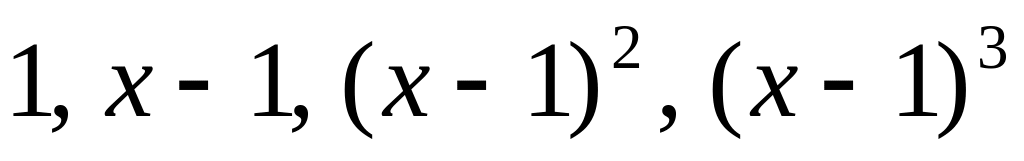 .
Ответ: f(2,–3,1,0).
.
Ответ: f(2,–3,1,0).
ЗАНЯТИЕ 8. Матрица перехода.
В векторном пространстве C над R найти матрицу перехода от базиса [1, i] к базису [2–i, 4i] и найти координаты вектора a=8+9i в новом базисе. Ответ:
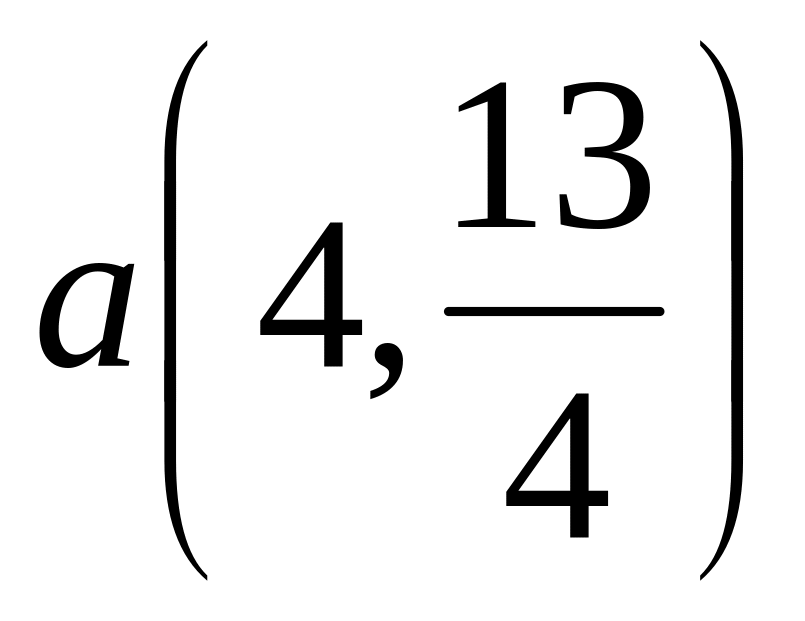 .
.В векторном пространстве
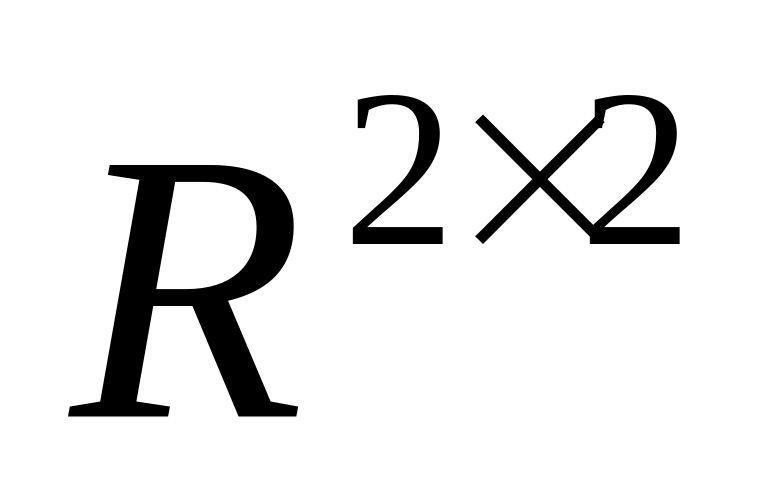 найти матрицу перехода от базиса
найти матрицу перехода от базиса
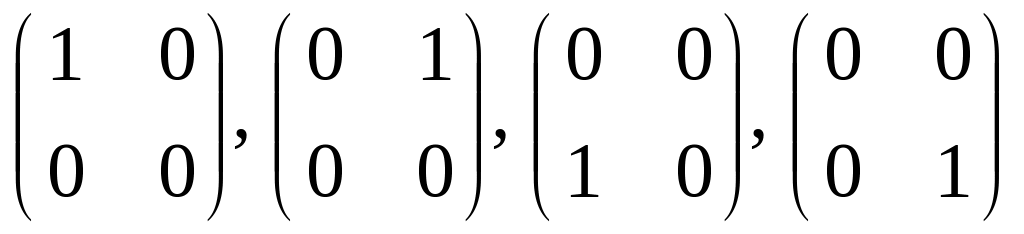 к базису
к базису
 и координаты вектора
и координаты вектора
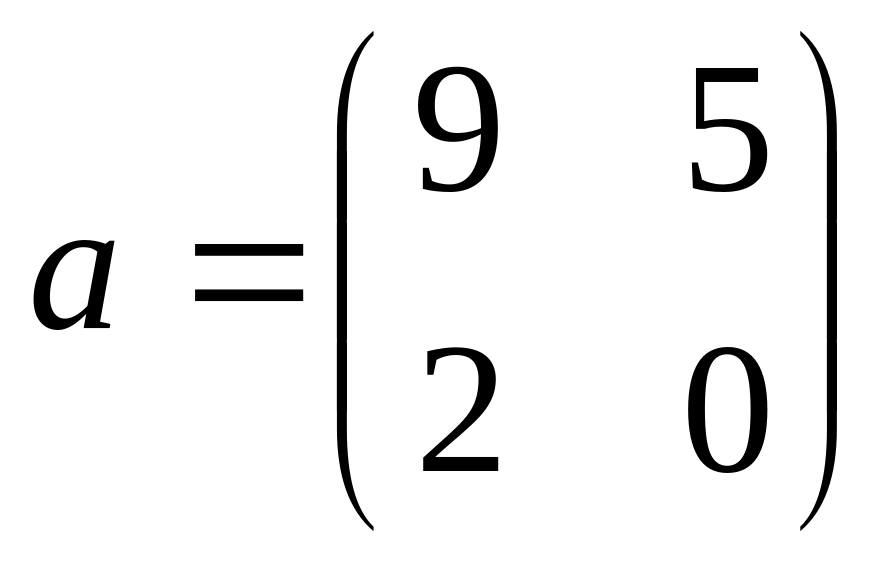 в новом базисе. Ответ: a(2,0,3,–1).
в новом базисе. Ответ: a(2,0,3,–1).Найти координаты вектора x в базисе
 ,
если известно его разложение по базису
,
если известно его разложение по базису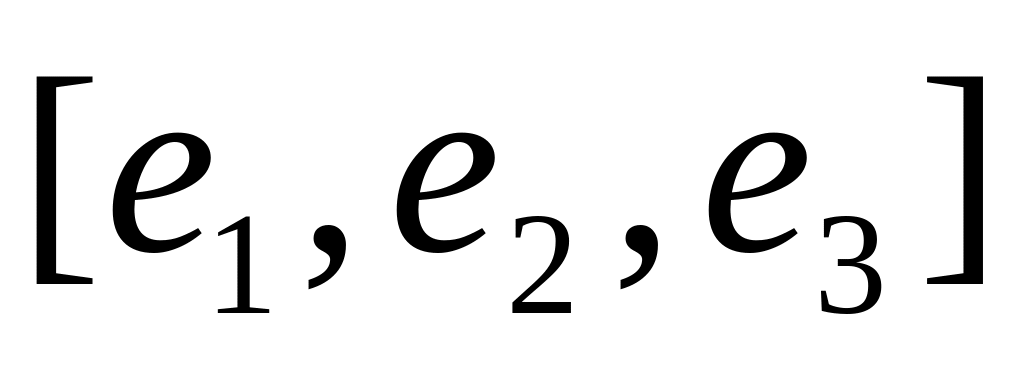 :
:
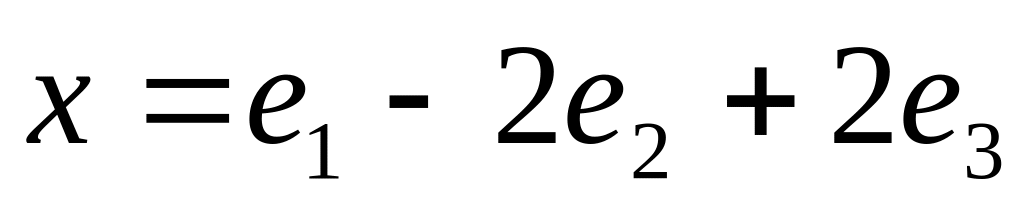 и
и
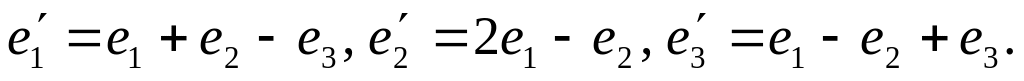 Ответ:
Ответ:
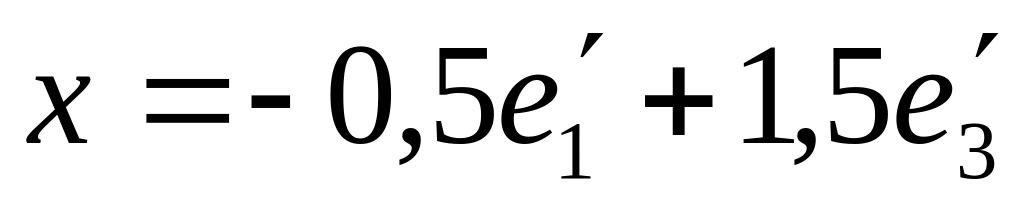 .
.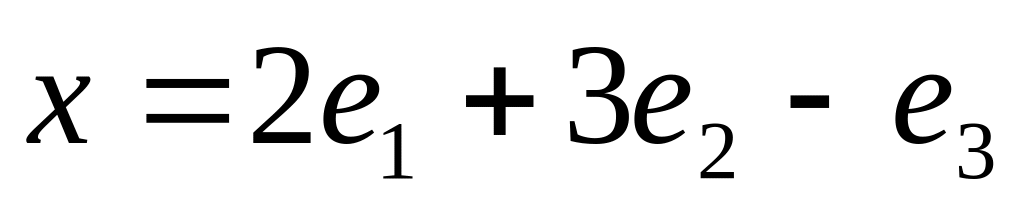 и
и
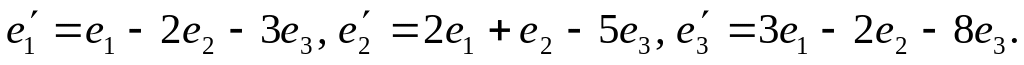 Ответ:
Ответ:
 .
.
В векторном пространстве
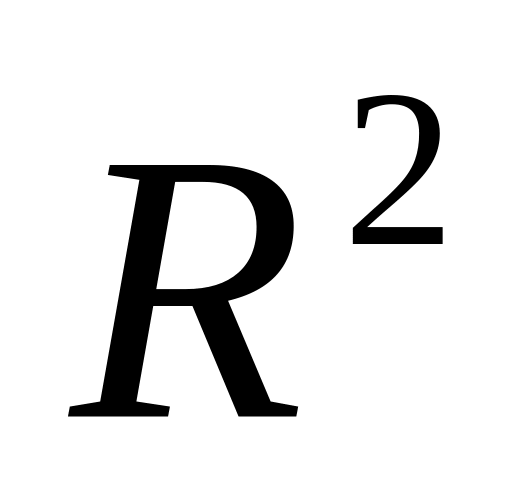 найти матрицу T
перехода от базиса
найти матрицу T
перехода от базиса
 к базису
к базису
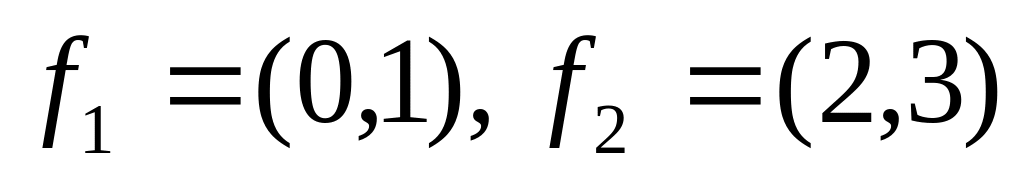 и координаты вектора
и координаты вектора
 в базисе
в базисе
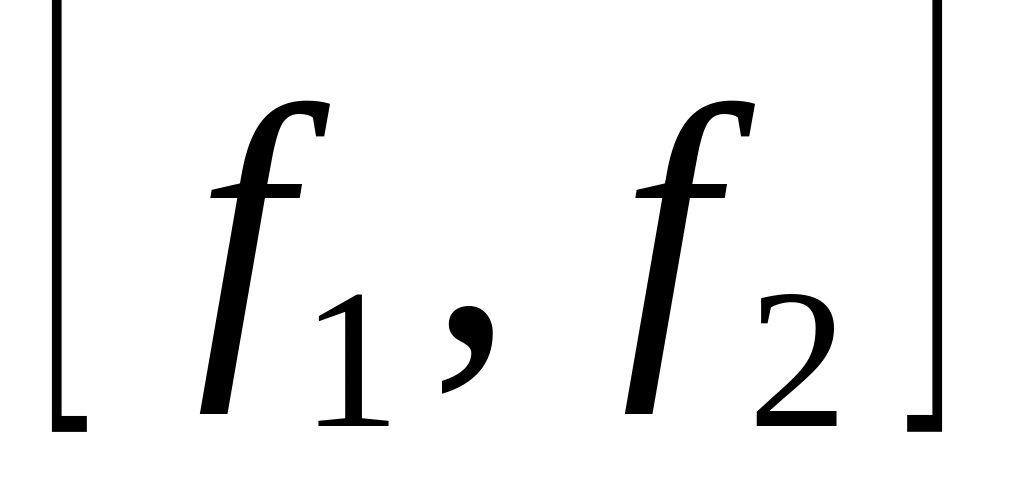 .
Ответ:
.
Ответ:
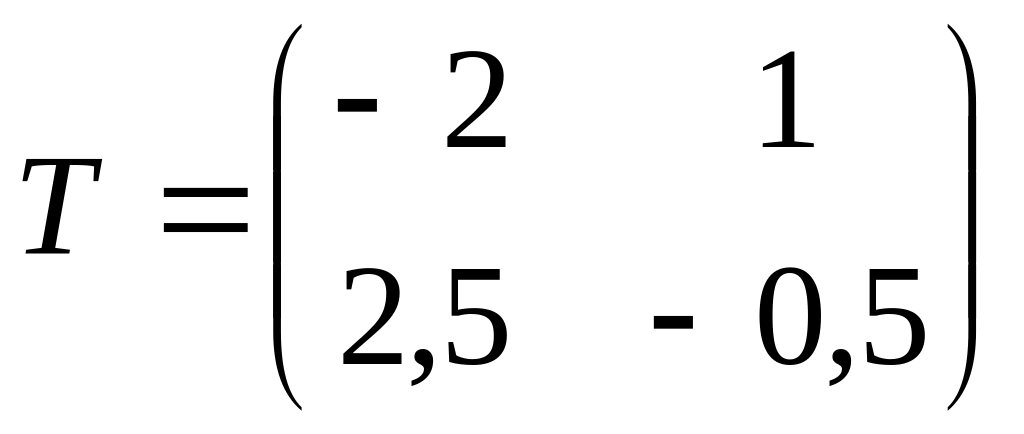 ,
,
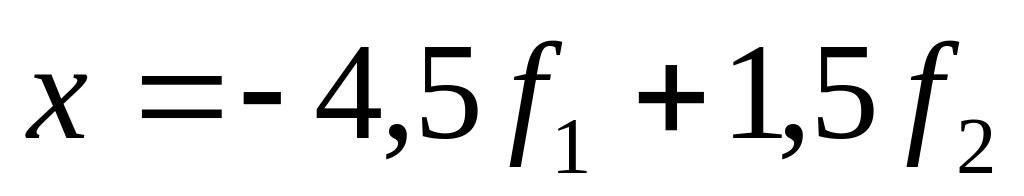 .
.В векторном пространстве найти матрицу T перехода от базиса
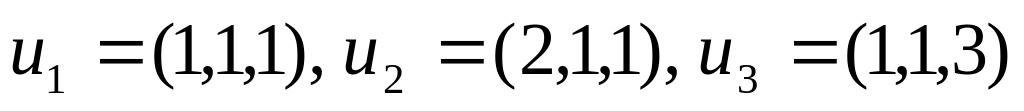 к базису
к базису
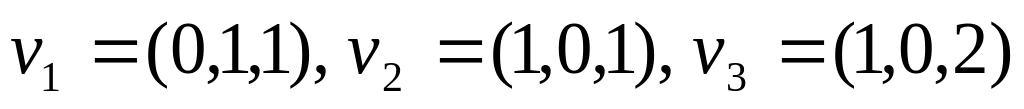 и координаты вектора
и координаты вектора
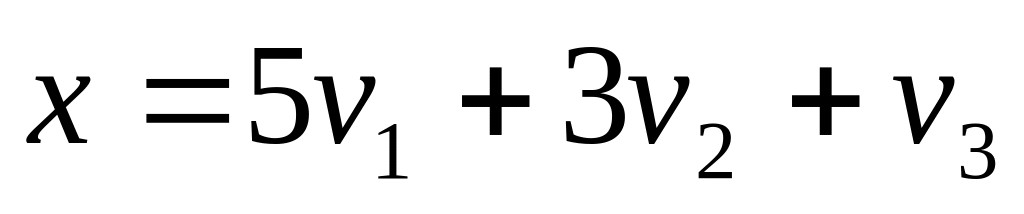 в базисе
в базисе
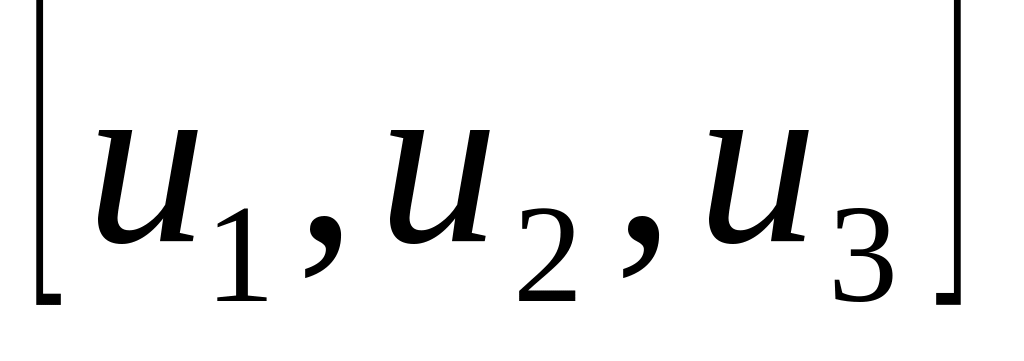 .
Ответ:
.
Ответ:
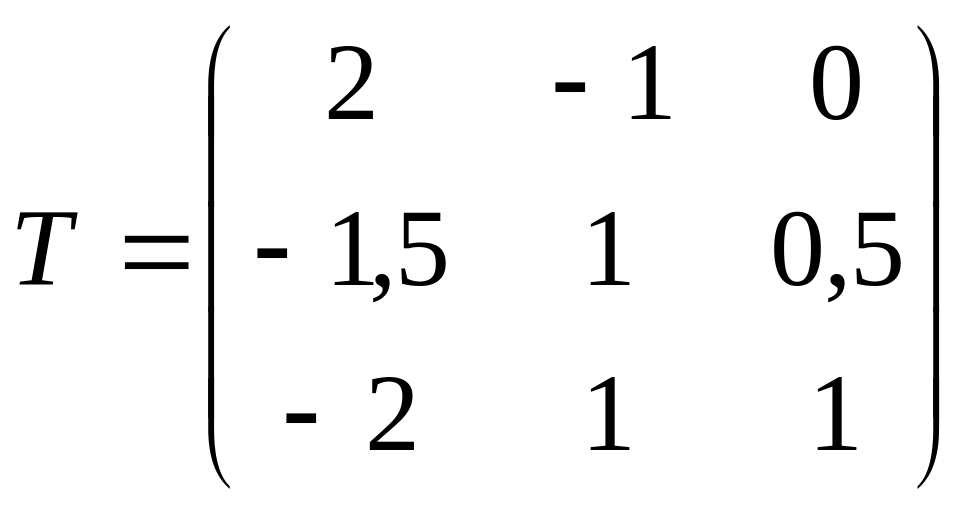 ,
,
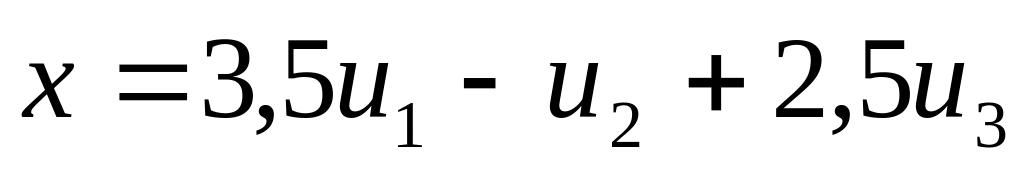 .
.Пусть
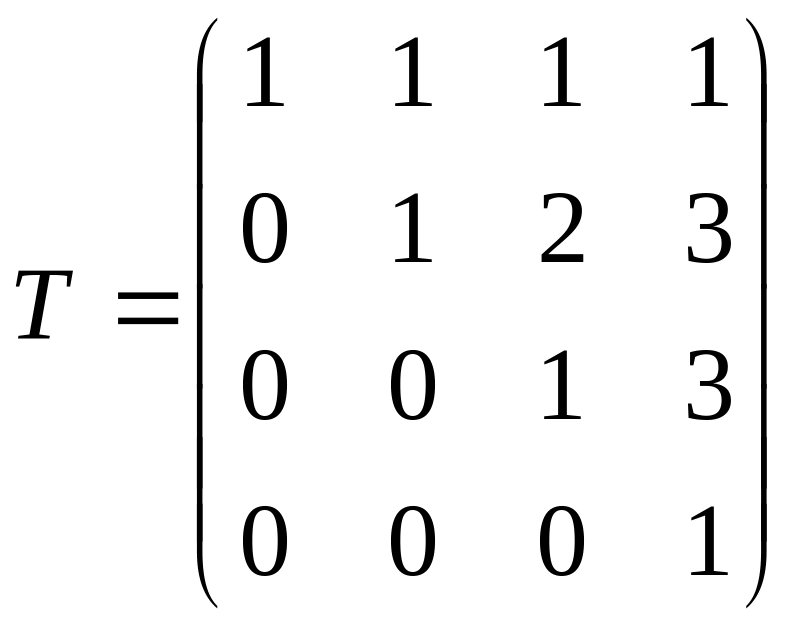 есть матрица перехода от базиса
есть матрица перехода от базиса
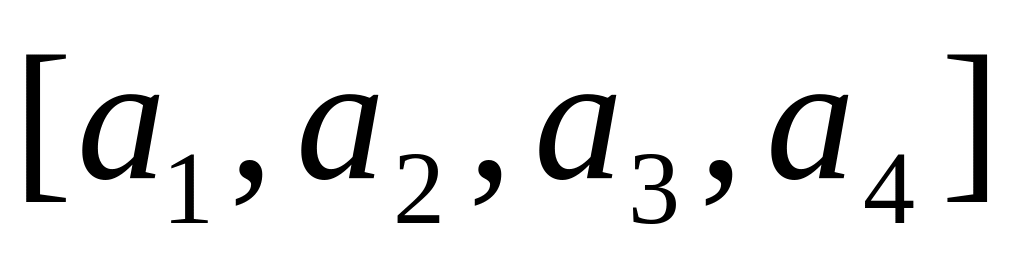 к базису
к базису
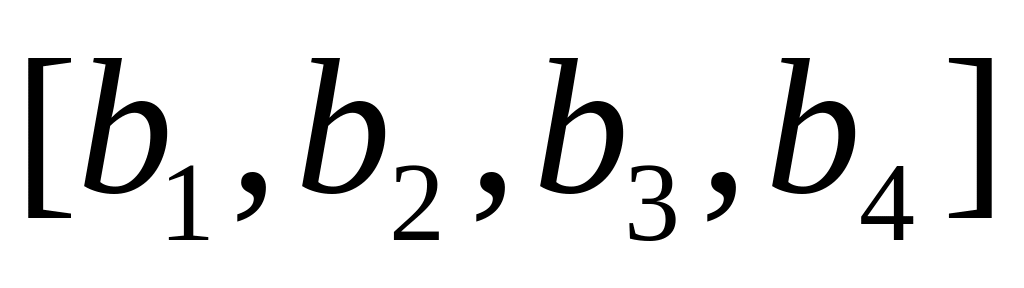 .
Найти координаты вектора
.
Найти координаты вектора
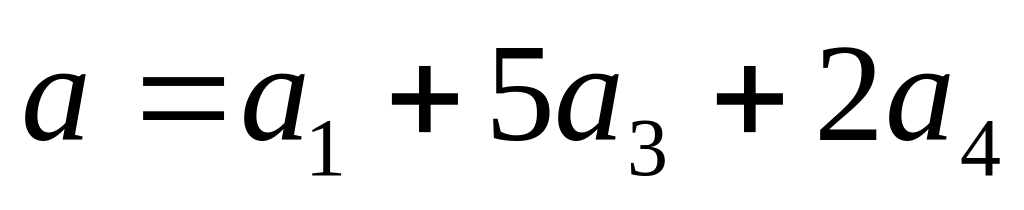 во втором базисе и координаты вектора
во втором базисе и координаты вектора
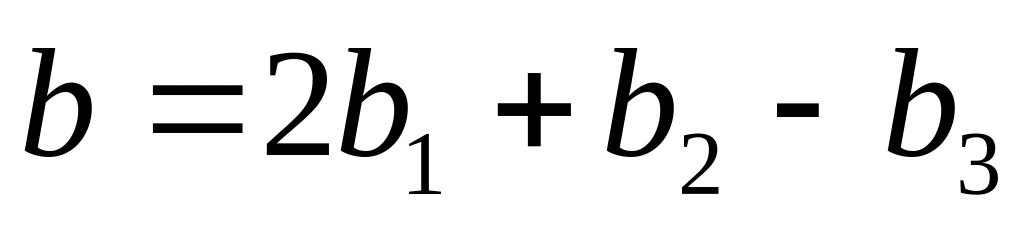 в первом. Ответ:
в первом. Ответ:
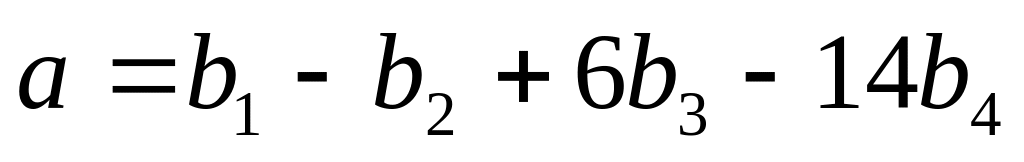 ,
,
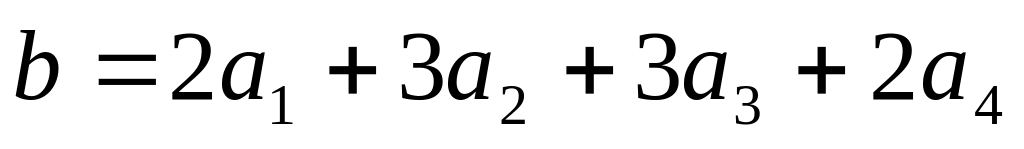 .
.
