Сравнение бесконечно малых функций

  Пусть α(x) и β(x) две бесконечно малые функции при x → x₀ и β(x) отлична от нуля в некоторой окрестности точки х₀ (за исключением, быть может, самой точки х₀). Если

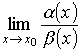= 0,

то α(x) называется бесконечно малой более высокого порядка, чем β(x) . В этом случае пишут α(x) = (β(x)) и говорят α(x) есть о − малое от β(x).   Если

= А ≠ 0 ( A - число),

то бесконечно малые α(x) и β(x) имеют одинаковый поряок малости. В этом случае пишут α(x) = (β(x)), (α(x) есть O - большое от β(x).    Если

= ∞,

то α(x) называется бесконечно малой более низкого порядка, чем β(x).    Если

= 1,

то α(x) и β(x) называется эквивалентными бесконечно малыми, α(x) ~ β(x).   В некоторых случаях недостаточно знать, что одна из двух бесконечно малых является бесконечно малой более высокого порядка, чем другая. Нужно еще оценить, как высок этот порядок. Поэтому вводится следующее правило: если

,

то α(x) является бесконечно малой n -го порядка относительно β(x).   Теорема. Для того, чтобы две функции f = f (x) и g = g (x), f (x) ≠ 0, g (x) ≠ 0, были эквивалентными при х → х₀, необходимо и достаточно, чтобы выполнялось хотя бы одно из условий

f - g = (f ) или f - g = (g).

21. Замечательные пределы. Следствия из 2-го замечательного предела.

1й замечательный предел:

Limsinx/x=1

x->0

2й з.п.

Lim(1+1/x)^x=e

х-> к бесконечности

lim(1+x)^1/x=e

х->0

Некоторые следствия из второго замечательного предела

       Существует несколько формул, которые можно вывести, используя второй замечательный предел. Например, найдем . В данном случае имеем неопределенность вида , раскрыть которую можно так:

Аналогично, можно получить такой результат:

или, в более общей форме:

атронем еще одно следствие из второго замечательного предела, которое используется не менее часто, нежели первое. Найдем . В данном случае мы имеем дело с той же неопределенностью , что и в предыдущем пределе. Однако для раскрытия рассматриваемой неопределенности требуется произвести замену. Примем , причем, учитывая , получим . Кроме того,

Учитывая всё вышесказанное, имеем:

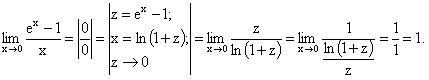
Данный результат можно записать в такой форме:

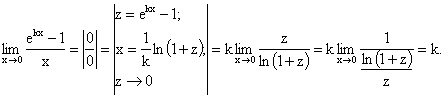
Обобщив предыдущую формулу, получим:

       

22. Непрерывность функции. Точки разрыва 1-го и 2-го рода.

функция непрерывна на интервале, если она непрерывна в каждой точке этого интервала.

разрыв 1-го рода(точка называется разрывом 1-го рода,если в этой т. Ф-ция имеет конечные но не равные друг другу левые и правые приделы)

разрыв 2-го рода(точка называется разрывом 2-го рода,если в этой т. Ф-ция не имеет хотя бы одного из односторонних приделов или один из них бесконечен)

23. Понятие производной. Геометрический , механический и экономический смысл.

Производной функцией в заданной точке называется предел отношения приращения функции к приращению аргумента при условии что прирощение аргумента х->0

С геометрической точки зрения,производная равна тангенсу угла наклона касательной к графику функции положительным направлением оси ОХ

С экономической точки зрения производная представляет собой момент времени u(t)- количество продукции за время t

производная от координаты по времени есть скорость. В этом состоит механический смысл производной. 24. Дифференцируемость и непрерывность функции.

-если функция у=f(x) имеет в некоторой точке производную, то она дифференцируема в этой точке

-если функция имеет производную в конечной точки интервала то она дифференцируема на интервале

Т]если функция у=f(x) дифференцируема в некоторой точке х, то она непрерывна в этой точке

! обратная теорема не верна т.е. из непрерывности НЕ следует ее дифференцируемость 25. Правила дифференцирования. Производная сложной функции. Производная суммы, произведения, частного.

1.У=f(u(x));u(x)-промежуточный аргумент

У’=f’u*u’ -производная сложной функции Правило дифференцирования суммы функций: Правило дифференцирования произведения функций (правило Лейбница): Правило дифференцирования частного функций: 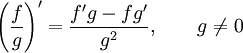26. Правила дифференцирования. Логарифмическое дифференцирование.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:

Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.

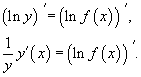
Отсюда видно, что искомая производная равна

Y=(u(x))^(w(x)) – степенно показательная

1 шаг: прологорифмировать

2 шаг:прологорифмировать обе части последнего равенства

3шаг: умножить на у обе части последнего равенства

4 шаг: у заменим на его первоначальное значение 27. Дифференциал функции. Свойства. .

Дифференциалом функции называется главная часть приращения функции, линейно зависящие от приращения аргументаю

Св-ва:

1. dc= 0, dc =c’-dx=0*dx=0

2. d(u+w+v)=du+dw-dv

3. d’(u*w)= w*du+u*dw

4. d’(u/w)=(wdu+udw)/w^2 28. Производные высших порядков. Дифференциалы высших порядков.

Второй производной функции называется производная от 1ой производной функции

Дифференциалом 2го порядка называется дифференциал от дифференциала 1го порядка по d^2=y’’*(dx)^2

29. Правило Лопиталя.

Для раскрытия непредельных выражений вида [0/0], [ / ]можно применять правило Лопиталя:

Если

1

  Пусть функции и непрерывны в некоторой окрестности точки и , то есть и при . Предположим, что при функции и имеют производные и , причём существует предел отношения этих производных:

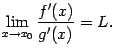
Тогда предел отношения самих функций и тоже существует и равен тому же числу :

30. Исследование функций. Интервалы монотонности.

Если на некотором интервале производная положительна, то функция возрастает. Если производная отрицательна, то на данном интервале функция убывает. Возрастание, убывание - интервалы монотонности

7) Ищутся точки перегиба и интервалы выпуклости.

Для определения точек перегиба находят вторую производную. В точке перегиба вторая производная равна нулю или не существует. По знаку второй производной в интервалах между точками перегиба определяют направление выпуклости графика функции. Если вторая производная положительна, то график функции выпуклый вниз. Если вторая производная отрицательная, то график функции выпуклый вверх.

На основании проведённого исследования строим график.

31. Экстремум функций. Необходимое и достаточное условия экстремума.

Т1](необходимое условие)

Пусть функция f(x) определена на интервале<a,b> и в (.) х0 имеет производную f’(x0)тогда f’(x0)=0

Точка, в которой f’(x)=0 называется стационарной точкой

Т2](достаточное условие)

1.если при переходе через критическую точку х0, 1ая производная функция сменяет знак и функция непрерывна в этой точки, то в этой точке есть экстремум, если

«-» на «+» -минимум

«+» на «-» -максимум

2.Если точка х0 стационарная точка функции и существует 2ая производная то в точке х0 будет минимум,если 2ая производная х0>0 и максимум если у’’(x0)<0 32. Исследование функций с помощью 2-ой производной. Выпуклость. Вогнутость. Точки перегиба.

Необходимое и достаточное условия существования точки перегиба. Нахождение экстремума с использованием 2-ой производной. Для определения точек перегиба находят вторую производную. В точке перегиба вторая производная равна нулю или не существует. По знаку второй производной в интервалах между точками перегиба определяют направление выпуклости графика функции. Если вторая производная положительна, то график функции выпуклый вниз. Если вторая производная отрицательная, то график функции выпуклый вверх.

  Необходимые условия наличия перегиба

      либо не существует.

     Достаточные условия наличия перегиба

     1. Если меняет знак при переходе через точку x₀, то x₀ - точка перегиба.

     2. Если то при n четном x₀ - точка перегиба, при n нечетном x₀ не является точкой перегиба.

Пусть функция f:U(x ₀ ) R, определенная в окрестности U(x ₀ ) точки х ₀ , имеем в х ₀ производные до порядка n включительно (n>1).

Если f’(x ₀ )=…=f ^(n-1) (x ₀ )=0 и f ⁽ⁿ⁾ (x ₀ )=0 , то при n нечетном в х ₀ экстремума нет, а при n четном экстремум есть, причем это строгий локальный минимум, если f ⁽ⁿ⁾ (x ₀ )>0 , и строгий локальный максимум, если f ⁽ⁿ⁾ (x ₀ ).

33. Асимптоты. Вертикальные, горизонтальные, наклонные. Их нахождение.

Асимптотой кривой у=f(x) называется прямая расстояние от которой до переменной точки М на кривой->0, при х-> к бесконечности

Наклонную асимптоту может быть найдена у=кх+в

При к=о, у=в-горизонтальная

Прямая с уравнением х=а называется вертикальной асимптотой если

Limf(x)=+-бесконечность

x->a 34. Общий план исследования функций и построения их графиков.

1.найти область определения функции

2.исследовать функцию на непрерывность

3.определить четность , не четность

4.определить точки пересечения с осями координат

5.найти 1ую и 2ую производные

6.найти промежутки возростания и убывания

7.найти экстремумы (max,min)

8.найти точки перегиба, интервала выпуклости, вогнутости

9.найти асимптоты графика

10.найти некоторые промежуточные точки графика

11.построить график начиная с асимптот, точек перегиба, точек max и min и точек перегиба с осями координат

35. Функции нескольких переменных. Область определения функции. Геометрический смысл функции 2-х переменных.

Область определения функции может быть открытой и замкнутой

область состоящая из одних внутренних точек называется открытой

если к области присоединяется точка на границы – замкнутая

число а0 называется приделом функции f(x,y) при х->х0, у->y0, если для всякого Е>0 найдется малое число е>0, такое что при выполнение условии близости (.)М(х,у)к(.)М0(х0,у0) будет выполнятся неравенство |f(x,y)-a0|<E

Переменная z (с областью изменения Z) называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Определение 1.2. Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.

Обозначения: z = f(x,y), z = z(x,y).