
21(1). Способы задания поверхности.
простая поверхность.
График
гладкой функции
![]() (1)
(1)
будем
называть простой
поверхностью. Например,
плоскость
![]() и параболоид
и параболоид
![]() .
.
2. параметр-ная поверхность. Пусть D - область на плоскости, и и v — декартовы координаты в D.
Уравнения
![]() ,
,![]() ,
,![]() ,
,
![]() (2)
(2)
где
![]() ,
,
![]() ,
,
![]() - гладкие ф-ции, определенные в
- гладкие ф-ции, определенные в
![]() ,
задают некоторое отображение (обозначим
его
,
задают некоторое отображение (обозначим
его
![]() )
этой области в трехмерное пространство
с декартовыми координатами
)
этой области в трехмерное пространство
с декартовыми координатами
![]() .
Точка
.
Точка
![]() называется регулярной
точкой отображения
,
если в ней ранг матрицы Якоби этого
отображения максимальный, т.е. равен
двум:
называется регулярной
точкой отображения
,
если в ней ранг матрицы Якоби этого
отображения максимальный, т.е. равен
двум:
![]() .
.
Точки области , в которых ранг < 2, называются нерегулярными точками отображения Ф.
Пусть
отобр. Ф является регулярным в т.
![]() .
.
теорема
(о
неявной ф-ции):
пусть
![]() - регулярная точка параметр-ной кривой,
заданной (2) . Тогда у точки
- регулярная точка параметр-ной кривой,
заданной (2) . Тогда у точки
![]() сущ-ет
-окрестность
из D,
такая, что образ этой окрестности при
отображении
представляет собой простую поверхность.
сущ-ет
-окрестность
из D,
такая, что образ этой окрестности при
отображении
представляет собой простую поверхность.
Тогда, пользуясь теоремой о неявной ф-ции, можно доказать, что у точки существует такая окрестность в области все точки которой (т.е. окрестности) явл-ся регулярными точками отображения Ф. Если отображение Ф имеет хотя бы одну регулярную точку, то образ V отображения Ф вместе с самим этим отображением называется гладкой параметризованной поверхностью. Переменные и и v называются параметрами или криволинейными координатами.
Пользуясь той же теоремой о неявной функции, можно доказать, что у точки сущ-ет такая окрестность в области , образ которой при отображении Ф является простой поверхностью, т.е. графиком. Т.о., параметр-ная поверхность как бы склеена из простых поверхностей.
Параметр-кие ур-я (2) в векторной форме
![]()
3. общая поверхность. Множество точек пространства, координаты которых связаны ур-ем
F(x, y, z) = 0 (3)
где F(x, y, z) - некоторая гладкая функция, назовем общей поверхностью. Точка М общей поверхности называется особой, если все три частные производные функции F(x,y,z) в этой точке обращаются в нуль:
![]()
![]() .
.
обычно предполагают, что общая пов-сть имеет хотя бы одну неособую точку М0. Тогда по теореме о неявной функции у этой точки существует такая окрестность в пространстве, внутри которой поверхность (3) представляет собой простую поверхность, то есть график некоторой функции z=f(x, y). Т.о., общая поверхность как бы склеена из простых поверхностей.
Если из параметрических ур-ний (2) исключить параметры и и v, то получим ур-е вида (3). Обратно, пусть дано ур-е (3). Зададим произвольно (гладкие) функции x(u,v) и y(u,v). Подставив их в ур-е (3), найдем ф-цию z(u,v). Полученные три ур-я вида (2) задают некот. параметризацию общей пов-ти (3).
Полагая в уравнениях (2) или (3)
u=u(t), v=v(t) (4)
мы
задаем на параметризованной поверхности
некоторую кривую, векторное ур-е которой
имеет вид
![]()
Ур-я (4) наз-ся внутр-ми ур-ми кривой на пов-ти.
Дифференцируя последнее уравнение, найдем касательный вектор кривой (4)
![]() (5)
(5)
Рассмотрим
равенство (5) в некоторой точке M(u,v)
поверхности
V.
Касательный
вектор в точке
M(u,v)
к
произвольной кривой на поверхности
явл. линейной комбинацией векторов
![]() и
и
![]() .
Т.о, касательные векторы ко всем кривым
на поверхности в регулярной точке M(u,
v)
лежат
в одной и той же плоскости, которая наз.
касательной
плоскостью к
пов-ти в точке M(u,v).
.
Т.о, касательные векторы ко всем кривым
на поверхности в регулярной точке M(u,
v)
лежат
в одной и той же плоскости, которая наз.
касательной
плоскостью к
пов-ти в точке M(u,v).
Векторы
и
образуют
базис в касат. пл-ти. Прямая, проходящая
через точку М
перпенд-но
касат-ой пл-ти, наз. нормалью
к
пов-ти V
в
точке М.
В
регулярной точке в качестве направляющего
вектора нормали можно взять векторное
произведение
![]() Корд-ми вектора
Корд-ми вектора
![]() являются миноры матрицы Якоби. Поэтому
канонические уравнения нормали имеют
вид
являются миноры матрицы Якоби. Поэтому
канонические уравнения нормали имеют
вид
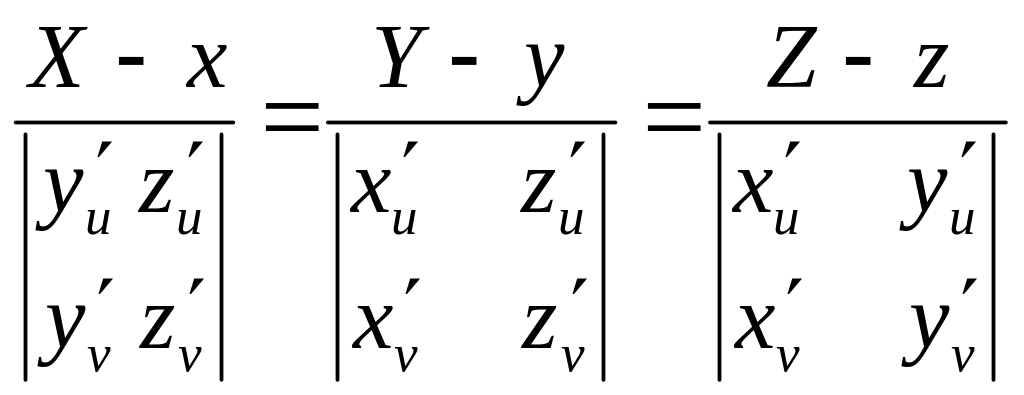 ,
,
а ур-ие
касат-ой пл-ти
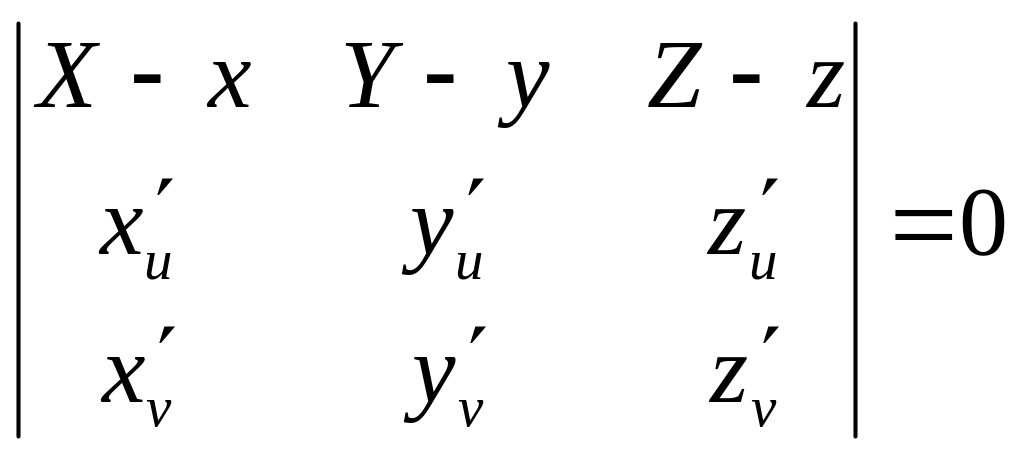
Здесь x, y, z - декартовы корд-ты т. М на пов-ти, X, У, Z — декартовы корд. текущей точки нормали или касательной плоскости.
Теорема. Вектор направлен перпендик.
касательной
плоскости, проведенной к поверхности,
в точке
![]() .
.
Док-во. F(x,y,z) = 0, но , , z=z(t), тогда F(x(t),y(t),z(t)) = 0. Продиф-руем по t и найдем значение в точке :
![]() ,
(6)
,
(6)
причем
![]() -
координаты вектора
,
лежащего в касательной плоскости, а
-
координаты вектора
,
лежащего в касательной плоскости, а
![]() координаты
вектора
.
тогда получается, что (6) – скалярное
произведение (
,
)=0,
а это означает перпендик-сть этих
векторов в плоскости, содержащей эти
векторы. Аналогичным образом можно
доказать перпендик-сть вектора
любому вектору из касательной плоскости,
проведенной в точке
,
что
и доказывает перпенд-сть вектора
касат. пл-сти.
координаты
вектора
.
тогда получается, что (6) – скалярное
произведение (
,
)=0,
а это означает перпендик-сть этих
векторов в плоскости, содержащей эти
векторы. Аналогичным образом можно
доказать перпендик-сть вектора
любому вектору из касательной плоскости,
проведенной в точке
,
что
и доказывает перпенд-сть вектора
касат. пл-сти.
Для
простоты записи, положим
![]() .
Тогда ур-е
касательной
плоскости для общей пов-сти в точке
:
.
Тогда ур-е
касательной
плоскости для общей пов-сти в точке
:
![]() .
.
ур-е нормальной плоскости для общей пов-сти в точке :
![]() .
.
