Геометрический метод

Минимизацию функций трёх или даже четырёх переменных можно эффективно выполнять, используя геометрическое представление логической функции. Все возможные комбинации значений n аргументов представляются как вершины n-мерного куба. Вершины, в которых функция равна единице, выделяются. Штрих справа от имени переменной означает её отрицание, для конъюнкции служит обычный знак умножения. Пример 3. Минимизируем функцию:

Рисунок 8 – Графическое представление ФАЛ

Единичные значения показаны жирными точками. Вершины куба соответствуют трёхчленным конъюнкциям аргументов, то есть трёхчленным элементарным конъюнкциям СДНФ, рёбра соответствуют двухчленным элементарным конъюнкциям ДНФ, полученным в результате минимизации СДНФ, а грани - единичному или нулевому значению какой-либо одночленной элементарной конъюнкции минимизированной ДНФ.

Из рисунка 5 видно, что две соседние вершины, например xy'z' и xyz', можно склеить. Формула ребра для оси-переменной не содержит этой переменной, так как значение функции на "склеенных" им вершинах не зависит от значения этой переменной, что соответствует операции выноса за скобки общего множителя.

Например, ребро xz' соединяет точки xy'z' и xyz': ( xy'z')+( xyz') = xz' (y'+y) = xz'

Минимизация с помощью n-мерного куба сводится к объединению максимума вершин, на которых функция принимает единичные значения, в минимум рёбер. Значит, минимальная ДНФ имеет вид:

Пример 4. Минимизируем функцию, состоящую из пяти членов:

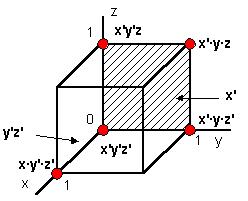
Рисунок 9 – Геометрическая интерпретация минимизации ФАЛ

На рисунке 9 вершины образуют грань куба. Формула этой грани состоит только из одной переменой - x', ось которой пересекает эта грань. В результате функция вместо пяти точек будет представлена гранью и ребром:

Метод Квайна

Метод минимизации Квайна У. (Quine W.V.) представляет собой локальный алгоритм, включающий определенную последовательность этапов []. Предполагается, что исходная минимизируемая функция задана в СДНФ.

ЭТАП 1. Нахождение первичных импликант.

Импликантой некоторой булевой функции называется другая булева функция, такая что множество нулевых значений импликанты N_имп.(0) пересекается со множеством нулевых значений функции N_f (0), а множество единичных значений N_имп.(1) принадлежит N_{f (1)}.

Первичной импликантой булевой функции называется такая импликанта, никакая часть которой не является импликантой исходной функции. На данном этапе рассматриваются все элементарные конъюнкции (ЭК) ранга n, первоначально входящие в СДНФ. Они попарно сравниваются между собой с целью нахождения поглощений вида:

Fx_i v Fx_i = F,

при которых получаются ЭК ранга (n – 1). После получения всех возможных ЭК ранга (n – 1) они вновь сравниваются попарно между собою для получения ЭК ранга (n – 2) и т.д. ЭК, принявшие участие в поглощениях, отмечаются некоторым символом. Процесс заканчивается тогда, когда полученные ЭК ранга m не склеиваются между собою. Все не отмеченные ЭК будут являться первичными импликантами.

(Для данного построения целесообразно использовать квадратные таблицы, размерностью l x l, где l – число ЭК k-го ранга; k = n, n – 1, ..., m.)

Например:

f (x₁, x₂, x₃, x₄, x₅) = x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅ v x₁x₂x₃x₄x₅

(Таблица исходных ЭК ранга 5 примет вид (табл. ).)

Выписываем ЭК 5-го ранга:

*x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅, *x₁x₂x₃x₄x₅

Образуем ЭК n-го ранга путем просмотра списка слева на право и попарного сравнения:

x₁x₂x₃x₅, x₁x₂x₄x₅, *x₁x₃x₄x₅, *x₂x₃x₄x₅, x₁x₂x₄x₅, x₂x₃x₄x₅, *x₂x₃x₄x₅, x₁x₂x₃x₄, *x₁x₂x₃x₄, *x₁x₃x₄x₅, *x₁x₃x₄x₅, *x₁x₂x₃x₄, *x₁x₂x₃x₅, *x₁x₂x₃x₅, *x₁x₂x₃x₄

ЭК принявшие участие в склеивании, помечаем знаком *.

Далее строим ЭК 3-го ранга:

x₃x₄x₅, x₃x₄x₅, x₁x₃x₄, x₁x₂x₃, x₁x₂x₃

Повторяющиеся ЭК исключаем из дальнейшего рассмотрения:

x₃x₄x₅, x₁x₃x₄, x₁x₂x₃

Образовать ЭК 2-го ранга невозможно, следовательно первичными импликантами являются:

x₁x₂x₃x₅, x₁x₂x₄x₅, x₁x₂x₄x₅, x₂x₃x₄x₅, x₁x₂x₃x₄, x₃x₄x₅, x₁x₃x₄, x₁x₂x₃

ЭТАП 2. Расстановка меток и нахождение существенных импликант.

В результате выполнения первого этапа минимизируем функция оказалась представленной в виде:

f (x₁, x₂, ..., x_n) = где l_i – первичные импликанты.

Для нахождения минимальной формы необходимо исключить некоторые первичные импликанты. Поэтому составляется таблица, строки которой соответствуют первичным импликантам, а столбцы ЭК исходной функции. Если в некоторую ЭК входит одна из первичных импликант, то на пересечении соответствующей строки и столбца ставится метка. Если после заполнения всей таблицы в некотором столбце оказывается только одна метка, то первичная импликанта, находящаяся в данной строке, называется существенной. (Табл.2)

В нашем случае существенными импликантами являются:

x₁x₂x₃x₅, x₁x₂x₄x₅, x₁x₂x₃x₄, x₃x₄x₅, x₁x₃x₄, x₁x₂x₃

Из таблицы исключаются строки, соответствующие существенным импликантам, и столбцы ЭК, покрываемых этими существенными импликантами (Табл.).

ЭТАП 3. Вычеркивание избыточных столбцов и избыточных первичных импликант.

Если в таблице полученной на предыдущем этапе имеются столбцы, в которых метки расположены в одинаковых строках, то один из таких столбцов вычеркивается. Так как покрытие оставшегося столбца будет осуществлять покрытие удаленной ЭК.

Если после удаления избыточных столбцов в таблице появляются строки, в которых нет ни одной метки, то они вычеркиваются, так как первичные импликанты, соответствующие этим строкам не покрывают оставшиеся в рассмотрении ЭК.

В нашем примере избыточные строки и столбцы отсутствуют.

Таблица 2.

x1x2x3x5

x1x2x4x5

x1x2x4x5

x2x3x4x5

x1x2x3x4

x3x4x5

x1x3x4

x1x2x3

Таблица 3.

	B1
x1x2x4x5
x2x3x4x5

A1 = x₁x₂x₃x₄x₅; A2 = x₁x₂x₃x₄x₅; A3 = x₁x₂x₃x₄x₅; A4 = x₁x₂x₃x₄x₅; A5 = x₁x₂x₃x₄x₅; A6 = x₁x₂x₃x₄x₅; A7 = x₁x₂x₃x₄x₅; A8 = x₁x₂x₃x₄x₅; A9 = x₁x₂x₃x₄x₅; A10 = x₁x₂x₃x₄x₅; A11 = x₁x₂x₃x₄x₅; A12 = x₁x₂x₃x₄x₅; A13 = x₁x₂x₃x₄x₅; B1 = x₁x₂x₃x₄x₅.

ЭТАП 4. Выбор минимального покрытия максимальными интервалами.

Из таблицы, полученной в результате выполнения третьего этапа, выбирается такая совокупность первичных импликант, которая включает хотя бы по одной метке в каждом столбце. При нескольких возможных вариантах выбирается покрытие минимальной сложности.

В рассматриваемом примере остается выбрать одну из первичных импликант.