
- •Криволинейный интеграл
- •Криволинейный интеграл первого рода
- •Криволинейный интеграл второго рода
- •1. Линейность:
- •3. Монотонность: если на , то
- •Поверхностные интегралы
- •Определение
- •Параметрическая форма
- •Свойства
- •Линейность:
- •Поверхностный интеграл второго рода Определение
- •Связь между поверхностными интегралами второго и первого рода
- •Свойства
- •Линейность:
- •Площадь поверхности
- •Длина кривой
- •Евклидово пространство
- •Длина дуги как параметр
- •Евклидова плоскость
- •Риманово пространство
- •Общее метрическое пространство
- •Формула Грина
- •Формула Гаусса – Остроградского
- •Формула Стокса
Поверхностные интегралы
Поверхностный интеграл первого рода
Определение
Пусть ![]() —
гладкая, ограниченная полная поверхность.
Пусть далее на
задана
функция
—
гладкая, ограниченная полная поверхность.
Пусть далее на
задана
функция
![]() .
.
Рассмотрим разбиение ![]() этой
поверхности на части
этой
поверхности на части
![]()
кусочно-гладкими кривыми и на каждой такой части выберем произвольную точку
![]() .
.
Вычислив значение функции в этой
точке ![]() и,
приняв за
и,
приняв за ![]() —
площадь поверхности
—
площадь поверхности ![]() рассмотрим
сумму
рассмотрим
сумму
![]() .
.
Тогда число ![]() называется
пределом сумм
называется
пределом сумм ![]() ,
если:
,
если:
![]()
Предел сумм
при ![]()
называется поверхностным интегралом
первого рода от функции ![]() по
поверхности
и
обозначается следующим образом:
по
поверхности
и
обозначается следующим образом:
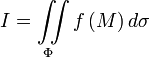
Параметрическая форма
Пусть на поверхности можно ввести единую параметризацию посредством функций
![]()
заданных в ограниченной замкнутой
области ![]() плоскости
плоскости ![]() и
принадлежащих классу
и
принадлежащих классу ![]() в
этой области. Если функция
непрерывна
на поверхности
,
то поверхностный интеграл первого рода
от этой функции по поверхности
существует
и может быть вычислен по формуле:
в
этой области. Если функция
непрерывна
на поверхности
,
то поверхностный интеграл первого рода
от этой функции по поверхности
существует
и может быть вычислен по формуле:
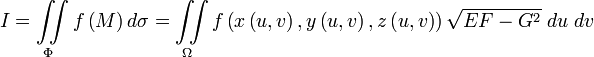 ,
где:
,
где:
![]()
![]()
![]()
Свойства
Из определения поверхностного интеграла первого рода следует независимость этого интеграла от выбора ориентации векторного поля единичных нормалей к поверхности или, как говорят, от выбора стороны поверхности.
Линейность:
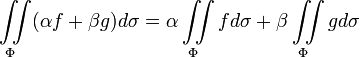 ;
;
Аддитивность:
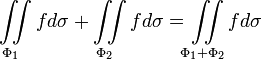 ;
;
Монотонность:
если
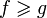 ,
то
,
то
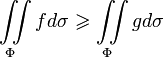
для
 если
если 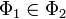 ,
то
,
то
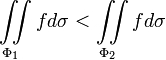
Теорема о среднем для непрерывной функции и замкнутой ограниченной поверхности :
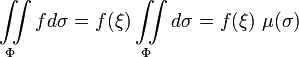 .
.
Поверхностный интеграл второго рода Определение
Рассмотрим двустороннюю поверхность , гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.
Для определенности предположим сначала,
что поверхность задана явным
уравнением ![]() причем
точка
причем
точка ![]() изменяется
в области
изменяется
в области ![]() на
плоскости
на
плоскости ![]() ,
ограниченный кусочно-гладким контуром.
,
ограниченный кусочно-гладким контуром.
Пусть теперь в точках данной
поверхности
определена
некоторая функция
.
Разбив поверхность сетью кусочно-гладких
кривых на части
и
выбрав на каждой такой части
точку
вычисляем
значение функции
в
данной точке и умножим его на
площадь ![]() проекции
на плоскость
элемента
,
снабженную определенным знаком. Составим
интегральную сумму:
проекции
на плоскость
элемента
,
снабженную определенным знаком. Составим
интегральную сумму:
![]() .
.
Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от
![]() ,
,
распространенным на выбранную сторону поверхности , и обозначают символом

(здесь ![]() )
напоминает о площади проекции элемента
поверхности на плоскость
)
напоминает о площади проекции элемента
поверхности на плоскость ![]()
Если вместо плоскости
спроектировать
элементы поверхности на плоскость ![]() или
или ![]() ,
то получим два других поверхностных
интеграла второго типа:
,
то получим два других поверхностных
интеграла второго типа:
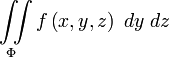 или
или 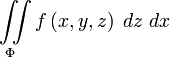 .
.
В приложениях чаще всего встречаются соединения интегралов всех этих видов:

где ![]() суть
функции от
суть
функции от ![]() ,
определенные в точках поверхности
.
,
определенные в точках поверхности
.
Связь между поверхностными интегралами второго и первого рода
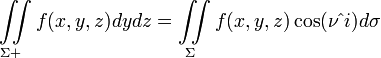 ,
,
где ![]() —
единичный вектор нормали поверхности
—
единичный вектор нормали поверхности ![]() ,
, ![]() —
орт.
—
орт.
Свойства
Линейность:
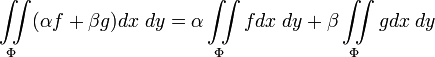 ;
;
Аддитивность:
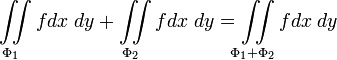 ;
;
При изменении ориентации поверхности, поверхностный интеграл меняет знак.
Площадь поверхности
Проще всего определяется
площадь многогранныхповерхностей:
как сумма площадейих
плоских граней.Чаще всего площадь
поверхности определяют для класса
кусочно гладких поверхностей с кусочно
гладким краем (или без края). Обычно это
делают с помощью следующей конструкции.
Поверхность разбивают на мелкие части
с кусочно гладкими границами: в каждой
части выбирают точку, в которой существует
касательная плоскость, и ортогонально
проектируют рассматриваемую часть на
касательную плоскость поверхности в
выбранной точке; площадь полученных
плоских проекций суммируют; наконец,
переходят к пределу при всё более мелких
разбиениях (таких, что наибольший из
диаметров частей разбиения стремится
к нулю). На указанном классе поверхностей
этот предел всегда существует, и если
поверхность задана параметрически
кусочно ![]() -гладкой
функцией
-гладкой
функцией ![]() ,
где параметры
,
где параметры ![]() ,
, ![]() изменяются
в области
изменяются
в области ![]() на
плоскости
на
плоскости ![]() ,
то площадь
,
то площадь ![]() выражается
двойным интегралом
выражается
двойным интегралом

где ![]() ,
,
![]() ,
,
![]() ,
,
a ![]() и
и ![]() —
частные производные по
и
.
—
частные производные по
и
.
В частности, если поверхность есть
график
-гладкой
функции ![]() над
областью
на
плоскости
над
областью
на
плоскости ![]() ,
то
,
то

На основе этих формул выводятся известные формулы для площади сферы и её частей, обосновываются приёмы для вычисления площади поверхностей вращения и т. п.
Для двумерных кусочно гладких поверхностей
в римановых
многообразиях эта
формула служит определением площади,
при этом роль ![]() ,
, ![]() ,
, ![]() играют
составляющие метрического
тензора самой поверхности.
играют
составляющие метрического
тензора самой поверхности.
