
- •Билет №1
- •Билет №2
- •Билет №3
- •Билет №4
- •Билет №5
- •Билет №6
- •Билет №7
- •Билет №8
- •Билет №9
- •Билет №10
- •Билет №11
- •Билет №12
- •Билет №13
- •Билет №14
- •Билет №15
- •Билет №16
- •Билет №17 Число опорных решений канонической задачи линейного программирования
- •Билет №18
- •Билет №19
- •Билет №20
- •Билет №21
- •Билет №22
- •Билет №23
- •Билет №24
- •Билет №25
- •Билет №26
- •Билет №27
- •Билет №28
- •Билет №29
- •Билет №30
- •Билет №31
- •Билет №32
Билет №23
Условия неограниченности целевой функции канонической задачи линейного программирования на минимум
Пусть симплекс
таблица приведена к некоторому базису
опорного решения α канонической задачи
линейного программирования (1)-(3) на
минимум. Если при этом существует столбец
As
с положительной
оценкой, т.е. ![]() где
s=1,2,…,n,
а все остальные элементы этого столбца
неположительные, т.е.
где
s=1,2,…,n,
а все остальные элементы этого столбца
неположительные, т.е. ![]() ,
i=1,2,…,r,
то целевая функция данной задачи
неограниченна на множестве допустимых
решений, и, следовательно, задача не
имеет оптимального решения.
,
i=1,2,…,r,
то целевая функция данной задачи
неограниченна на множестве допустимых
решений, и, следовательно, задача не
имеет оптимального решения.
Доказательство.
Пусть симплекс таблица приведена к базису А1,А2,…,Ar опорного решения α=(α1,α2, …,αr, 0,0, …, 0) и имеет вид :
A’1 |
A’2 |
… |
A’r |
A’r+1 |
… |
A’s |
… |
A’n |
B’ |
1 |
0 |
… |
0 |
a1,r+1 |
… |
a1s |
… |
a1n |
α1 |
0 |
1 |
… |
1 |
a2,r+1 |
… |
a2s |
… |
a2n |
α2 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
0 |
0 |
… |
1 |
ar,r+1 |
… |
ars |
… |
arn |
Αr |
0 |
0 |
… |
0 |
|
… |
|
… |
|
|
Следовательно, вектор ограничений В’ , а так же вектор условий A’s можно представить в виде линейной комбинации базисных векторов, а именно :
(12) A’1α1 + A’2α 2 +…+A’r α r =B и
A’1α’1s
+ A’2α’
2s +…+A’r
α’
rs =
A’s
![]()
(13)
A’1α’1s
+ A’2α’
2s +…+A’r
α’
rs
–A’s
=
![]() .
.
Помножив соотношение
(13) на переменную t![]() и вычтя его из соотношения (12), получим:
и вычтя его из соотношения (12), получим:
A’1 (α1 – ta’1s) + A’2 (α 2 – ta’2s) +…+A’r (α r – ta’rs) + A’st = B’
Из последнего
соотношения и с учетом того, что a’is
![]() 0,
следует что вектор At
= (α1
– ta’1s
, α
2 – ta’2s,
…,α
r
– ta’rs,
0, …, 0, t,
0, …, 0) является допустимым решение
задачи (1)-(3). По лемме о целевой функции
для допустимого решения αе
имеем
0,
следует что вектор At
= (α1
– ta’1s
, α
2 – ta’2s,
…,α
r
– ta’rs,
0, …, 0, t,
0, …, 0) является допустимым решение
задачи (1)-(3). По лемме о целевой функции
для допустимого решения αе
имеем
f(αt)
= f(α)
- ![]() (α1
– ta’1s)
+
(α1
– ta’1s)
+ ![]() 2
(α
2 – ta’2s)
-…-
r
(α
r –
ta’rs)
-
st.
2
(α
2 – ta’2s)
-…-
r
(α
r –
ta’rs)
-
st.
С учетом того что
оценки базисных векторов равны нулю,
то есть
![]() 2
=…=
r
= 0, значение целевой функции можно
записать в виде : f(αt)
= f(α)
-
.
Так как
то
при t
2
=…=
r
= 0, значение целевой функции можно
записать в виде : f(αt)
= f(α)
-
.
Так как
то
при t
![]() целевая функция неограниченно уменьшается,
то есть f(αt)
целевая функция неограниченно уменьшается,
то есть f(αt)![]() ,
и, следовательно, задача не имеет
оптимального решения.
,
и, следовательно, задача не имеет
оптимального решения.
Билет №24
Решение канонической задачи линейного программирования на минимум симплекс методом, критерии выбора вектора вводимого в базис и выводимого из базиса
Рассмотрим каноническую задачу линейного программирования.
(9)
f(X)=![]() +
+![]()
(10)
![]() =B
=B
(11)
![]() ,
j=1,2,…,n.
,
j=1,2,…,n.
Пусть вектор α опорное решение данной задачи. Выберем некоторый базис этого опорного решения, например, В1,…,Bl,…,Bk,…,Br, т.е. опорное решение имеет вид α=(0,…,0,α1,0,…,0,αl,0,…,0,αk,0,…,0,αr,0,0,…,0).
Приведя систему векторов условий к базису выбранного опорного решения, получим симплекс таблицу (4)
… |
B1 |
… |
Bl |
… |
Bk |
… |
Br |
… |
As |
… |
B |
… |
1 |
… |
0 |
… |
0 |
… |
0 |
… |
a’1s |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
0 |
… |
1 |
… |
0 |
… |
0 |
… |
a’ls |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
0 |
… |
0 |
… |
1 |
… |
0 |
… |
a’ks |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
0 |
… |
0 |
… |
0 |
… |
1 |
… |
a’rs |
… |
|
… |
0 |
… |
0 |
… |
0 |
… |
0 |
… |
|
… |
|
Если любой вектор системы условий задачи в полученной симплекс таблице имеет неположительную оценку т.е.
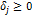 для всех j=1,2,…,n
то опорное решение α является оптимальным
решением данной задачи ( теорема о
достаточном условии оптимальности
опорного решения).
для всех j=1,2,…,n
то опорное решение α является оптимальным
решением данной задачи ( теорема о
достаточном условии оптимальности
опорного решения).Если в симплекс таблице существует s-й столбец с положительной оценкой
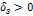 ,
где s=1,2,…,n
а все остальные элементы s-го
столбца неположительные то целевая
функция данной задачи неограниченна
на множестве допустимых решений и
следовательно задача не имеет оптимального
решения (теорема о неограниченности
целевой функции)
,
где s=1,2,…,n
а все остальные элементы s-го
столбца неположительные то целевая
функция данной задачи неограниченна
на множестве допустимых решений и
следовательно задача не имеет оптимального
решения (теорема о неограниченности
целевой функции)
Если оценка s-го столбца положительная, но при этом среди элементов этого столбца найдется положительный т.е. ais
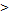 0,
i=1,2,…,r.
То рассматриваются соотношения вида
0,
i=1,2,…,r.
То рассматриваются соотношения вида
 для
всех a’is
0
, среди которых выбирается наименьшее.
Пусть это будет отношение
для
всех a’is
0
, среди которых выбирается наименьшее.
Пусть это будет отношение 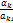 =
=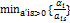 .
Затем проводится преобразование Жордана
симплекс таблицы (4) с разрешающим
элементом
.
Затем проводится преобразование Жордана
симплекс таблицы (4) с разрешающим
элементом 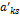 . После такого преобразования будет
получена новая симплекс таблица
приведенная к базису отличному от
предыдущего так как вектор Bk
уступил
место вектору As.
Эта симплекс таблица обладает свойствами
: 1)она приведена к базису
B1,…,Bl,…,Bk-1,Bk+1,…,Br,…,As.
2)Все элементы столбца ограничений
неотрицательные.
. После такого преобразования будет
получена новая симплекс таблица
приведенная к базису отличному от
предыдущего так как вектор Bk
уступил
место вектору As.
Эта симплекс таблица обладает свойствами
: 1)она приведена к базису
B1,…,Bl,…,Bk-1,Bk+1,…,Br,…,As.
2)Все элементы столбца ограничений
неотрицательные.
