Линейная алгебра.

Матрицы.

Матрицей называется квадратная или прямоугольная таблица, заполненная числами. Эти числа называются элементами матрицы.

· Элементы матрицы, расположенные по горизонталям, образуют

строки матрицы.

· Элементы матрицы, расположенные по вертикалям, образуют

столбцы матрицы.

Виды матриц.

Некоторые часто встречающиеся виды матриц имеют собственные названия:

1. квадратная матрица, 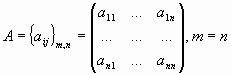, матрица, у которой одинаковое число строк и столбцов;

2. матрица-строка, 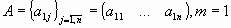матрица, у которой одна строка;

3. матрица-столбец, 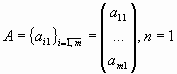, матрица, у которой один столбец;

4. диагональная матрица, 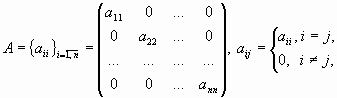квадратная матрица, у которой все внедиагональные элементы раны нулю;

5. единичная матрица, диагональная матрица, у которой все диагональные элементы — единицы нулю; 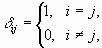— называется символом Кронекера;

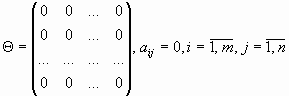6. нулевая матрица, , матрица, все элементы которой — нули;

7. верхняя треугольная матрица, 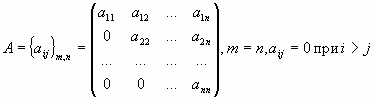, квадратная матрица, у которой все элементы, расположенные ниже диагонали — нули;

8. нижняя треугольная матрица, 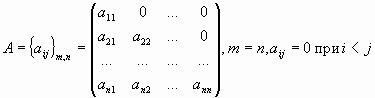, квадратная матрица, у которой все элементы, расположенные выше диагонали — нули;

9. ступенчатая матрица, 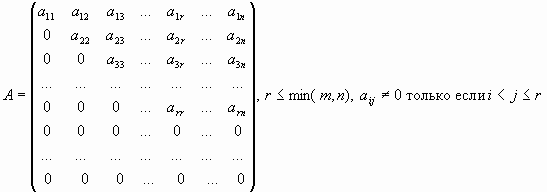и др

Действия над матрицами :

умножение на число,

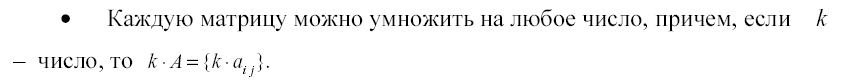
сложение,

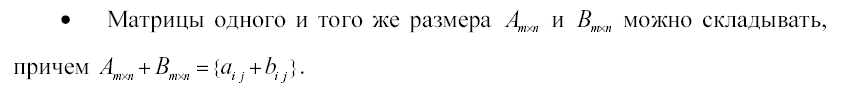
произведение матриц ,

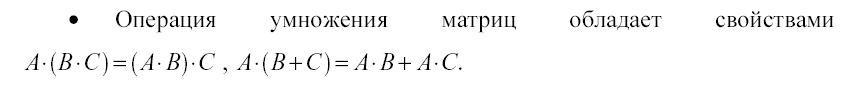
транспонирование. Транспонированием матрицы 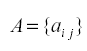называется операция, результатом которой является матрица

Определители второго и третьего порядка.

Алгебраические дополнения и миноры.

Определители n-го порядка

Свойства определителей

• Определитель не изменяется при транспонировании: det A^T = det A.

• При перестановке любых двух строк, определитель меняет знак.

• Если в определителе есть две одинаковые строки, то он равен нулю.

• Если все элементы строки определителя умножить на отличное от нуля число, то определитель умножается на это число:

• Определитель с двумя пропорциональными строками равен нулю.

• Определитель, содержащий нулевую строку, равен нулю.

• Если каждый элемент какой либо строки определителя представлен в виде суммы двух слагаемых:

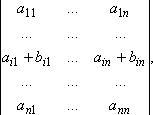
то его можно представить в виде суммы двух определителей:

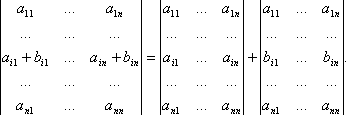
• Определитель не изменится, если к элементам любой его строки прибавить элементы

любой другой строки, умноженные на одно и то же число.

Поскольку определитель не меняется при транспонировании, приведенные выше утвкрждерия

справедливы и для столбцов.

Обратная матрица.

Пусть A — квадратная матрица порядка n:

Если существует квадратная матрица X той же размерности, что и матрица A, удовлетворяющая соотношениям A·X = X·A = I, то матрица A называется обратимой, а матрица X называется обратной к матрице A и обозначается A⁻¹.

Здесь I — единичная матрица соответствующей размерности:

A·A⁻¹ = A⁻¹·A = I.

Всякая невырожденная матрица A имеет единственную обратную матрицу

A_ij — алгебраическое дополнение элемента a_ij матрицы A.

Необходимое и достаточное существование обратной матрицы.

Теорема условия существования обратной матрицы

Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.

Матрица А = (А1, А2,...А_n) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы r . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.

Ранг матрицы и его связь с линейной независимостью строк или столбцов.

Наивысший порядок отличных от нуля миноров матрицы называется рангом матрицы.

То есть, если ранг матрицы равен r, то среди миноров матрицы порядка r есть хотя бы один, отличный от нуля, а все миноры матрицы более высоких порядков равны нулю.

Обозначаем Rg A, rg A, rank A. Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) матрицы. То есть, если ранг матрицы равен r, то среди строк (столбцов) матрицы есть r линейно независимых строк (столбцов), а любые r +1 строки (столбца) — линейно зависимы.

Матрицы, имеющие одинаковый ранг — подобные матрицы. Элементарные преобразования не меняют ранга матрицы. Ранг ступенчатой матрицы равен количеству ненулевых строк.

Матричная запись системы n линейных уравнений с n неизвестными.

Теорема Крамера для системы n линейных уравнений с n неизвестными.

Теорема. Если определитель матрицы системы n линейных алгебраических уравнений относительно n неизвестных отличен от нуля, то система имеет единственное решение, которое вычисляется по формулам:

, где D = det A ? 0 — определитель матрицы системы, а D _i — определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом правых частей:

Метод обратной матрицы для решения линейных уравнений.

!!!!!!

Метод Гаусса

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:

1. Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.

2. Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.

3. Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.

4. Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.

5. Далее заново переходят к пункту 1

Теорема Кронскера-Капелли

Теорема Кронекера-Капелли утверждает, что система уравнений

имеет решение тогда и только тогда, когда ранг её расширенной матрицы совпадает с рангом матрицы

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Система линейных однородных уравнений: фундаментальная система уравнений.

Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением.

Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-r линейно независимых решений.

Совокупность n-r линейно независимых решений однородной системы называется фундаментальной системой решений. Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицы A однородной линейной системы Ax=0 меньше числа неизвестных n и векторы

e₁ , e₂ , ..., e_n-r образуют ее фундаментальную систему решений (Ae_i =0, i=1,2, ..., n-r), то любое решение x системы Ax=0 можно записать в виде x=c₁ e₁ + c₂ e₂ + ... + c _n-r e_n-r ,

где c₁ , c₂ , ..., c_n-r — произвольные постоянные. Записанное выражение называется общим решением однородной системы.

Структура общего решения системы m линейных уравнений с n неизвестными.

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Понятие о линейном операторе.

Оператор , действующий в линейных пространствах называется линейным оператором, если и для любых и для любого числа .

Если пространства и совпадают, то говорят, что оператор действует в пространстве . В дальнейшем ограничимся рассмотрением линейных операторов, действующих в линейном пространстве .

Матрица оператора.

Рассмотрим линейный оператор , действующий в конечномерном линейном пространстве , и пусть базис в . Обозначим через образы базисных векторов .

Матрица

столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве.