Лекция № 5.

Тема: СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ

Основные вопросы, рассматриваемые на лекции:

1. Совершенная дизъюнктивная нормальная форма

2. Совершенная конъюнктивная нормальная форма

3. Теорема о существовании и построении СДНФ

4. Теорема о существовании и построении СКНФ

Краткое содержание лекционного материала

Дизъюнктивная (конъюнктивная) нормальная форма от n переменных p₁, …, p_n называется совершенной, если ее конъюнкты (дизъюнкты) не повторяются и в каждом конъюнкте (дизъюнкте) содержится ровно один литерал от переменных p₁,…, p_n. Обозначение: СДНФ (СКНФ).

Каждая СДНФ (СКНФ) от n переменных содержит не более 2ⁿ попарно различных конъюнктивных (дизъюнктивных) одночленов.

Формула B называется СДНФ (СКНФ) формулы A, если AB и B есть СДНФ (СКНФ). Для каждой формулы A, отличной от противоречия (тавтологии), существует СДНФ A (СКНФ A).

СДНФ от n переменных p₁, …, p_n формулы A (содержащей переменные p₁, …, p_n) можно найти, используя таблицу истинности для A.

В таблице истинности выделим строки с A1, и по-новому их перечислим: 1,2,…,m, где 1m2ⁿ. Через h_ij мы обозначим значение истинности в i-й строке переменной p_j, а через (p_ij)* обозначим переменную p_j (отрицание переменной p_j), если h_ij1 (соответственно, h_ij0), где i1,…,n, j1,…,m.

Лемма 1. (p_ij)*1 равносильно p_jh_ij для всех i1,…,n, j1,…,m.

Доказательство. Если h_ij1, то (p_ij)*p_j, p_j1, откуда (p_ij)*1, p_jh_ij.

Если h_ij0, то (p_ij)*p_j, p_j0, откуда, вновь, (p_ij)*01, p_jh_ij. 

Теорема 1. Если формула A не противоречие, то существует СДНФ A.

Доказательство. Если A не противоречие, то найдется хотя бы одна строка с номером m, где 1m2ⁿ. Используя также лемму 1, получим следующую цепочку эквивалентных предложений (для краткости вместо слова «эквивалентно» пишем знак ):

.

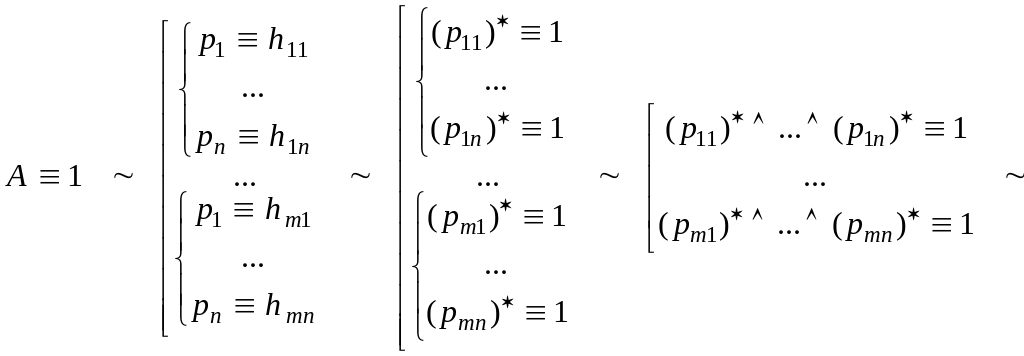
Значит, ((p₁₁)*…(p_1n)*)…((p_m1)*…(p_mn)*) есть СДНФ A.

Напомним, что: AB равносильно AB.

Теорема 2. Если формула A не тавтология, то существует СКНФ A.

Доказательство. Если A не тавтология, то A не противоречие. Применим к A теорему 1: A((p₁₁)*…(p_1n)*)…((p_m1)*…(p_mn)*) (литералы (p_1n)* выбираются из строк, в которых A1, т.е. A0).

Через (p_ij)* обозначим переменную p_j (отрицание переменной p_j), если (p_ij)* есть p_j (соответственно, (p_ij)* есть p_j), где i1,…,n, j1,…,m.

Легко увидеть, что (p_ij)*(p_ij)*.

Применим законы де Моргана и получим СКНФ A:

A[((p₁₁)*…(p_1n)*)…((p_m1)*…(p_mn)*))]

((p₁₁)*…(p_1n)*)…((p_m1)*…(p_mn)*)

((p₁₁)*…(p_1n)*)…((p_m1)*…(p_mn)*)

((p₁₁)*…(p_1n)*)…((p_m1)*…(p_mn)*).

Лекция № 6.

Тема: ПОЛНЫЕ СИСТЕМЫ СВЯЗОК

Основные вопросы, рассматриваемые на лекции:

1. Число булевых функций

2. Одноместные и двухместные булевы функции

3. Функции, определимые в терминах данной системы функций

4. Полные и неполные системы связок

Краткое содержание лекционного материала

Истинностные функции также называются булевыми функциями или логическими связками. Всего существует 2²ⁿ n-местных булевых функций.

Одноместных булевых функций имеется всего четыре:

постоянная функция h₁(A)1,

постоянная функция h₂(A)0,

тождественная функция h₃(A)A,

отрицание h₄(A)A.

Двухместных булевых функций имеется всего 16:

постоянная функция h₁(A,B)1,

постоянная функция h₂(A,B)0,

проекция первой координаты h₃(A,B)A,

проекция второй координаты h₄(A,B)B,

отрицание первой координаты h₅(A,B)A,

отрицание второй координаты h₆(A,B)B,

эквивалентность h₇(A,B)AB,

отрицание эквивалентности (связка «либо…, либо») h₈(A,B)(AB),

дизъюнкция h₉(A,B)AB,

отрицание дизъюнкции (стрелка Пирса) h₁₀(A,B)AB(AB),

конъюнкция h₁₁(A,B)AB,

отрицание конъюнкции (штрих Шеффера) h₁₂(A,B)AB(AB),

импликация h₁₃(A,B)AB,

отрицание импликации h₁₄(A,B)(AB),

обратная импликация h₁₅(A,B)AB,

отрицание обратной импликации h₁₆(A,B)(AB).

Функция H называется определимой в терминах функций f₁,…,f_k, если:

1) H есть одна из функций f₁,…,f_k;

2) H(x₁,…,x_n)G(*₁,…,*_m), где G – функция, определимая в терминах f₁,…,f_k, а *₁,…,*_m – одна из переменных x₁,…,x_n или тоже функция, определимая в терминах f₁,…,f_k.

Например, связка  определима в терминах  и , так как xyxy. Тождественная функция I(x)x определима в терминах , так как xxx.

Система функций f₁,…,f_k называется полной системой связок, если любая истинностная функция определимая в терминах f₁,…,f_k. Ясно, что n-местные функции D(x₁,…,x_n)x₁…x_n и C(x₁,…,x_n)x₁…x_n определимы соответственно в терминах  и . Отсюда и из теорем 1 и 2 следует, что система связок , ,  – полная система связок. Используя законы де Моргана, можно показать, что системы ,  и ,  – тоже полные системы связок.

Заметим, что если любая истинностная функция определима в терминах g₁,…,g_l, а каждая из связок g₁,…,g_l определима в терминах f₁,…,f_k, то любая истинностная функция также определима в терминах f₁,…,f_k.

Пример. Полнота системы связок ,  означает, что любая булева функция определима в терминах  и . Связки  и  определимы в терминах  и : 0xx, xx0, xyxy(xy).

Следовательно, любая булева функция определима в терминах  и , т.е. ,  – полная система связок.