Директрисы фигуры эллипс

 

С фигурой эллипс связаны две прямые, называемые директрисами . Их уравнения:

x = a / e ; x = - a / e .

Теорема. Для того, чтобы точка лежала на границе фигуры эллипс, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

 

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину фигуры эллипс, заданного уравнением :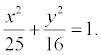 

 

•  Координаты нижней вершины: x = 0; y² = 16; y = -4.

•  Координаты левого фокуса: c² = a ² – b² = 25 – 16 = 9; c = 3; F₂ (-3; 0).

•  Уравнение прямой, проходящей через две точки:

 

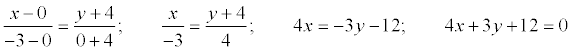
Пример. Составить уравнение границы фигуры эллипс, если его фокусы F ₁ (0; 0), F₂ (1; 1), большая ось равна 2.

 

Уравнение границы имеет вид: 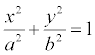 . Расстояние между фокусами:

2 c =  , таким образом, a² – b² = c² = 1/2

по условию 2а = 2, следовательно а = 1, b = 

Итого искомое уравнение имеет вид:  .

 Фокальные радиусы: 

Свойства эллипса.

Теорема. (Свойства эллипса.)

1. В канонической для эллипса системе координат, все

    точки эллипса находятся в прямоугольнике

                                 ,  .

2. Точки   лежат на

    эллипсе.

3. Эллипс является кривой, симметричной относительно

    своих главных осей.

4. Центр эллипса является его центром симметрии.

   Доказательство. 1, 2) Сразу же следует из канонического уравнения эллипса.

3, 4) Пусть М(х, у) – произвольная точка эллипса. Тогда ее координатыудовлетворяют уравнению (4). Но тогда координаты точек   также удовлетворяют уравнению (4), и, следовательно, являются точками эллипса, откуда и следуют утверждения теоремы.

Теорема доказана.

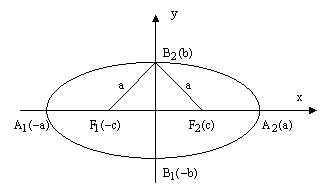
                                          рис.3.

Определение. Величина 2а называется большой осью эллипса, величина а называется большой полуосью эллипса.

Определение. Величина 2b называется малой осью эллипса, величина b называется малой полуосью эллипса.

Определение. Точки пересечения эллипса с его главными осями называются вершинами эллипса.

3.17 Гипербола (рис. 4.15) 

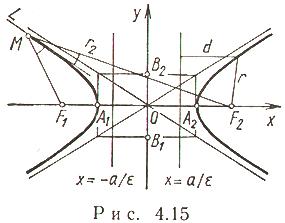
     Пусть на плоскости заданы две точки   и     и дано число a (0 < a < c). Гипербола - множество точек M плоскости, для каждой из которых модуль разности расстояний от точек   и   равен 2a. Точки   и   называются фокусами гиперболы;   - действительная ось;   - мнимая ось; O - центр;   - левый и правый фокусы;   - вершины;   - фокальные радиусы: 

     Каноническое уравнение: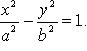 

     Эксцентриситет: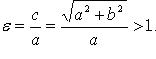 

     Фокальные радиусы:

       для правой ветви 

       для левой ветви 

     Фокальный параметр: 

     Уравнения директрис: 

Свойства

• Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

  • Иначе говоря, если   и 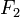  фокусы гиперболы, то касательная в любой точки 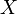  гиперболы является биссектрисой угла  .

• Для любой точки лежащей на гиперболе отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.

• Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.

• Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.

3.18  Парабола(рис. 4.16)

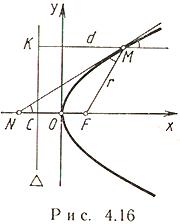
     Пусть на плоскости заданы точка F и прямая  , не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой  . Точка F называется фокусом, прямая   - директрисой параболы; (OF) - ось, O - вершина,   - параметр,   - фокус,   - фокальный радиус.

     Каноническое уравнение: 

     Эксцентриситет: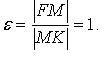 

     Фокальный радиус: 

     Уравнение директрисы: 

     Уравнение касательной в точке