
- •Понятие матрицы. Виды записи.
- •Классификация матриц.
- •Действия с матрицами. Свойства. Сложение и вычитание.
- •Умножение на число.
- •Произведение матриц.
- •Определители. Свойства определителей. Определители 2-го порядка.
- •Определители 3-го порядка.
- •Невырожденные матрицы. Обратная матрица.
- •Ранг матрицы.
- •Вычисление ранга по определению.
- •Элементарные преобразования.
- •Собственные числа. Собственные векторы матрицы.
- •Некоторые приложения в экономике собственных чисел и собственных векторов матрицы.
- •Линейные модели обмена.
- •Модель международной торговли
- •Решение.
- •Индивидуальные задания.
- •Варианты.
- •Варианты.
- •Содержание
Умножение на число.
Произведением матрицы А=(аij) на число k называется матрица В=(bij) такая, что bij=k..aij (i= , j= ).
Пример 4:
А=![]() ,
k=4,
А.k=
,
k=4,
А.k=![]() .
.
Матрица –А=(-1).А называется противоположной матрице А.
Свойства умножения матриц на число:
 .А=
.А=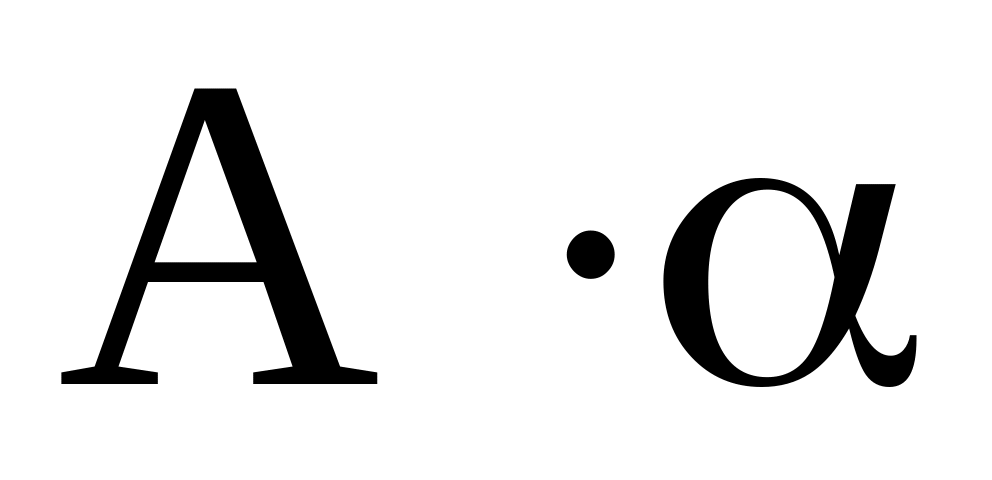
.(А+В)=
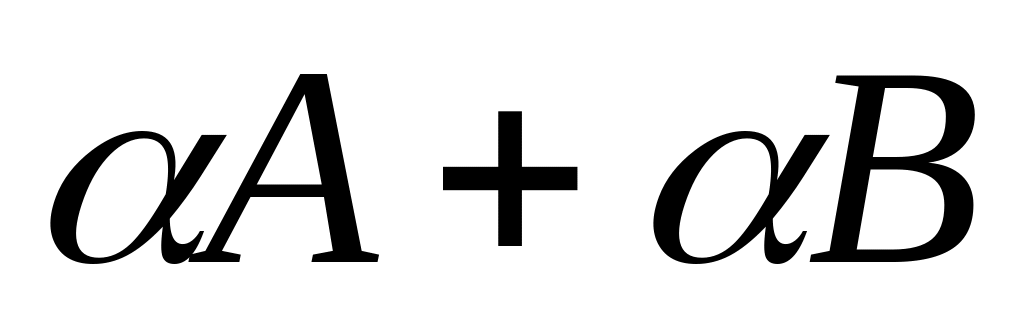 ;
;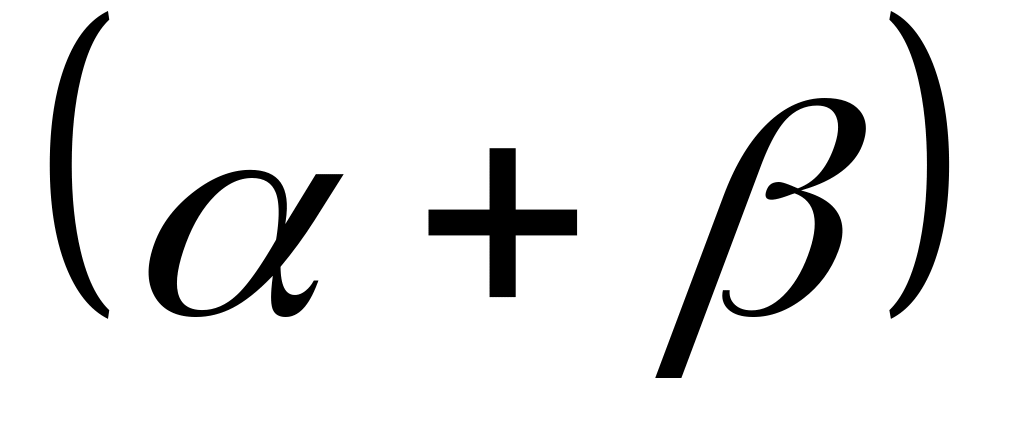 .А=
.А=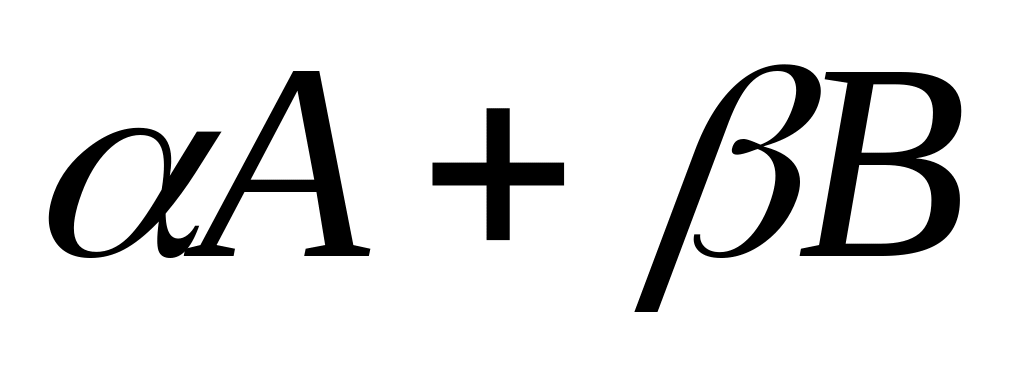 ;
;.(
 )=(
)=( ).А,
).А,
где
А, В- матрицы,![]() -числа.
-числа.
Произведение матриц.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы Аm n=(aij) на матрицу Bn p=(bjk) называется матрица Сm p=(cik) такая, что
cik=ai1 .b1k+ai2 .b2k+…+ain .bnk
Пример 5: Группировка продаж по различным филиалам фирмы «Башмачок» представлена таблицей:
Таблица 3.
-
Филиалы
Вид продукции и его цена (руб.)
I (2 тыс.)
II (3 тыс.)
III (5 тыс.)
Продано единиц
Продажа за рубежом.
Розничная продажа
Продажа другим фирмам
7
54
45
9
60
52
6
30
20
Выручка от продаж фирмы запишется:
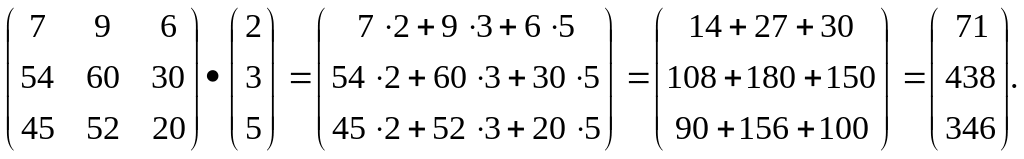
Из данного примера видно, что при умножении двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица-множимое, и столько столбцов, сколько их имеет матрица-множитель.
В общем виде:
 ;
;
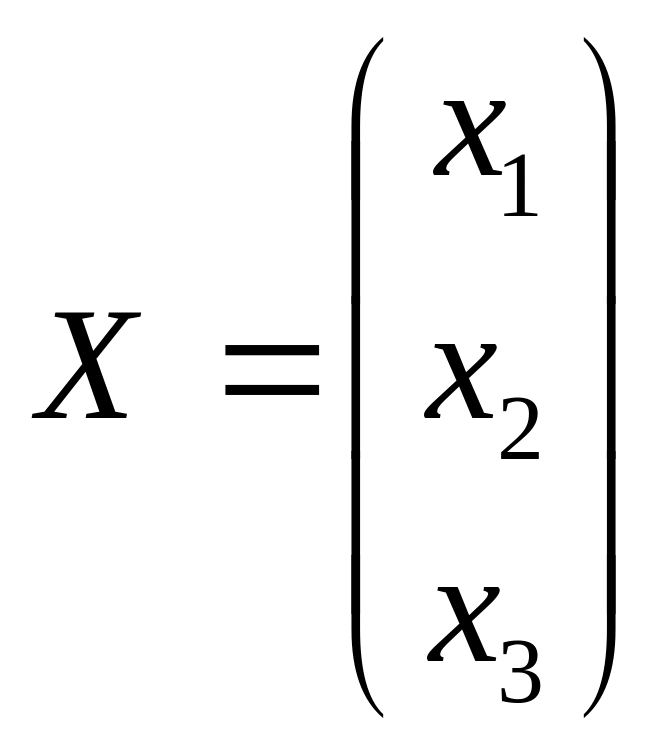 ;
;
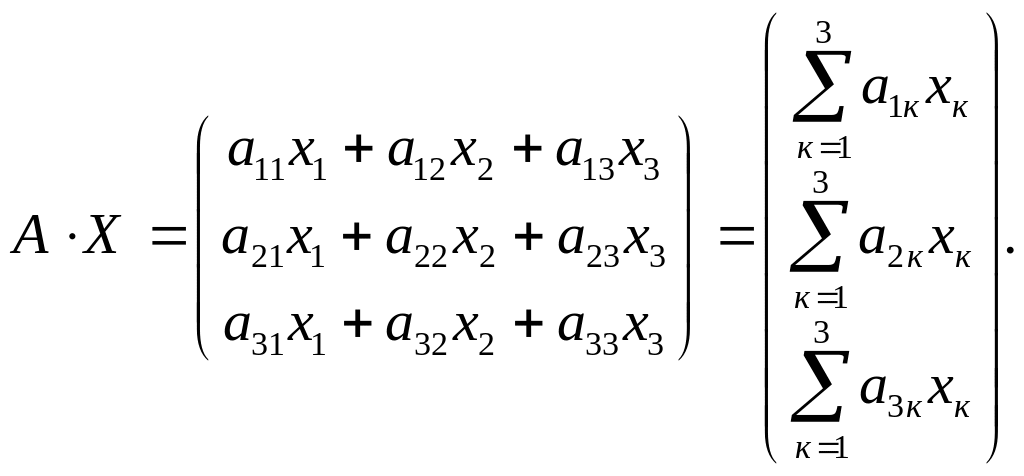
Матрицы А и В называются перестановочными, если АВ=ВА, в противном случае равенство не верно.
Свойства умножения матриц:
АВ
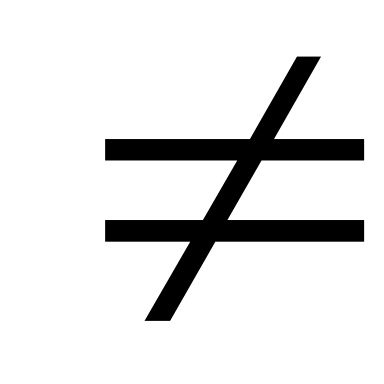 ВА
ВАА.(В.С)=(А.В).С;
А.(В+С)=АВ+АС;
(А+В).С=АС+ВС;
(АВ)=( А)В.
Транспонированная матрица обладает следующими свойствами:
(АТ)Т=А;
(А+В)Т=АТ+ВТ;
(АВ)Т=ВТ .АТ.
Определители. Свойства определителей. Определители 2-го порядка.
Рассмотрим квадратную матрицу 2-го порядка
А= .
Определителем
2-го порядка,
соответствующим матрице А,
называется число, равное а11.а22
– а12.а21
и обозначается
![]() или detА
(детерминант
А).
или detА
(детерминант
А).
![]() .
.
Элементы матрицы А называются элементами определителя . Элементы а11, а22 образуют главную диагональ, а элементы а21а12 – второстепенную (правую).
Определители 3-го порядка.
Рассмотрим квадратную матрицу 3-го порядка
.
Определителем 3-го порядка, соответствующим матрице А, называется число
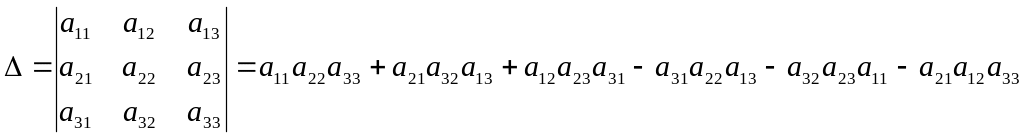 .
.
Данное правило вычисления определителя 3-го порядка называется правилом треугольников или правилом Саррюса, которое символически можно записать так:
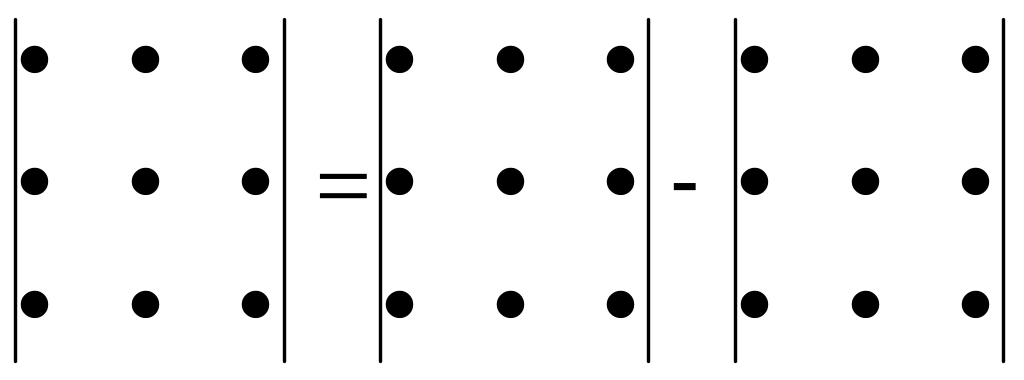


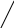
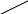


 .
.
Определители n-го порядка.
Пусть дана квадратная матрица n-го порядка
А=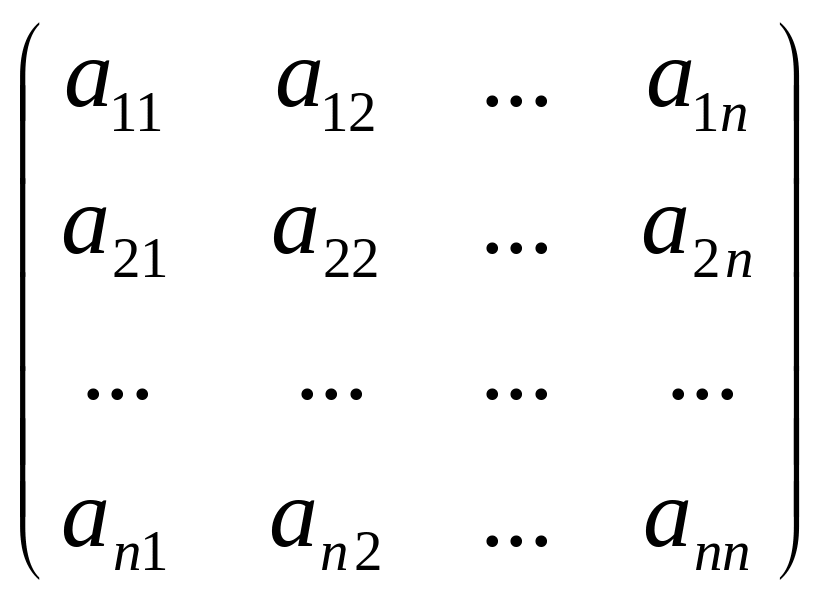 .
.
Определители n-го порядка, соответствующий матрице А обозначается
![]()
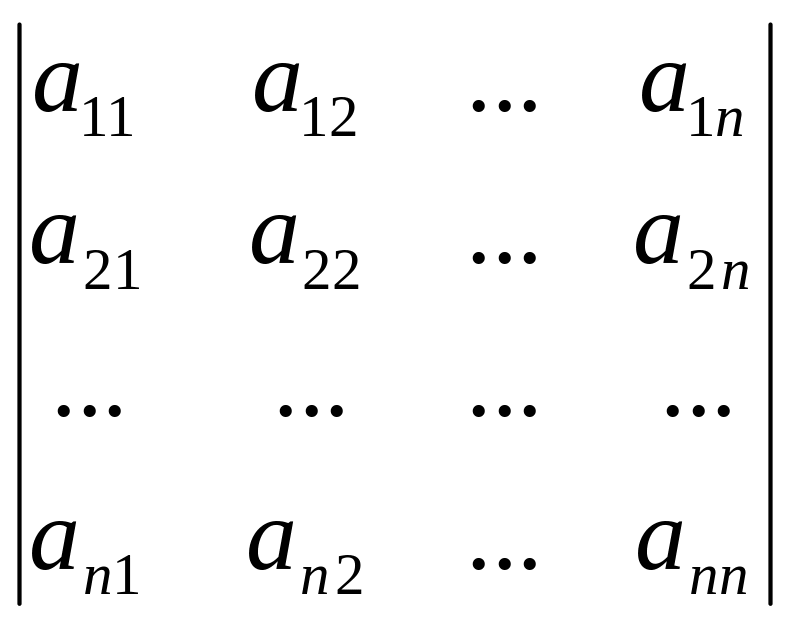 .
.
Минором Мij элемента аij определителя называется определитель (n-1)-го порядка, который получается из определителя путём вычёркивания i-строки и j-столбца.
Алгебраическим дополнением (адъюнктом) элемента аij определителя называется произведение минора Мij этого элемента на множитель (-1)i+j.
Определители
n-го
порядка
(n![]() )
называется число
=
)
называется число
=![]() ,
где аij-элемент
i-ой
строки, Аij-
алгебраическое дополнение этого элемента
(i=
,
где аij-элемент
i-ой
строки, Аij-
алгебраическое дополнение этого элемента
(i=![]() ).
).
Свойства определителей
(«Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот, т.е.:
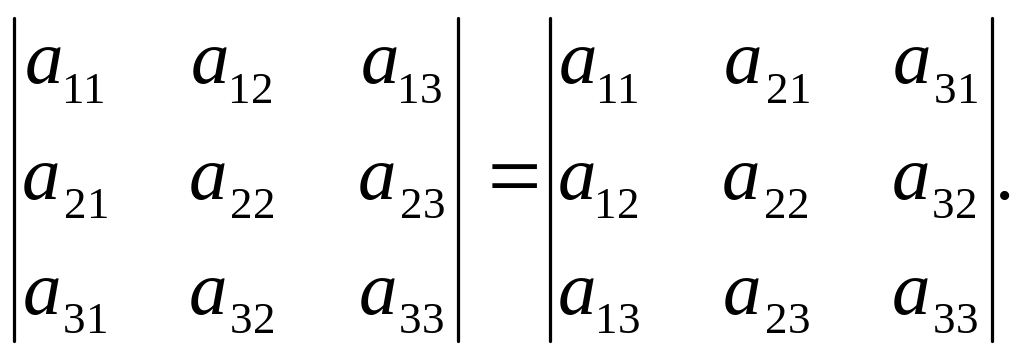
В дальнейшем строки и столбцы будем просто называть рядами определителя.
При перестановке двух параллельных рядов определитель меняет знак.
Определитель, имеющий два одинаковых ряда, равен нулю.
Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

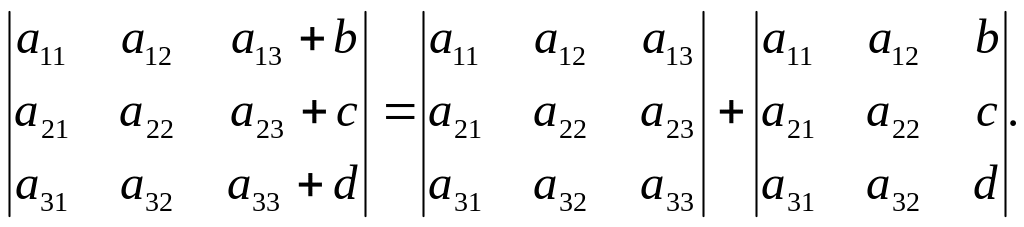
(«Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и тоже любое число.
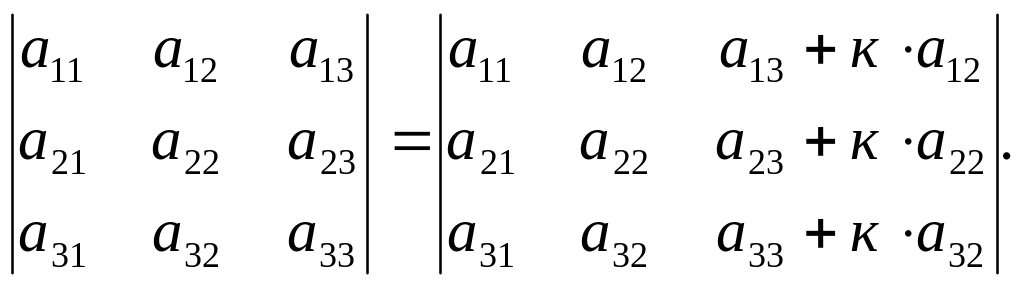
(«Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.


Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
![]()
