§ 3.7. Проверка гипотез относительно равенства средних, t- Критерий Стьюдента
Задача сравнения средних двух генеральных совокупностей возникает, когда практическое значение имеет именно величина исследуемого признака. Например, когда сравниваются сроки лечения двумя различными методами, или количества осложнений, возникающих при их применении. В этом случае можно использовать t-критерий Стьюдента.
Постановка задачи.
Получены две выборки {Х1} и {X2},
извлеченные из генеральных совокупностей
с нормальным законом распределения
и одинаковыми дисперсиями. Объемы
выборок n1 и n2,
выборочные средние равны
,
а выборочные дисперсии –
,
соответственно. Требуется сравнить
между собой генеральные средние.
Проверяемые гипотезы:
Н0 – генеральные средние одинаковы;
Н1 – генеральные средние различны.
Показано, что в случае справедливости гипотезы Н0 величина t, вычисляемая по формуле
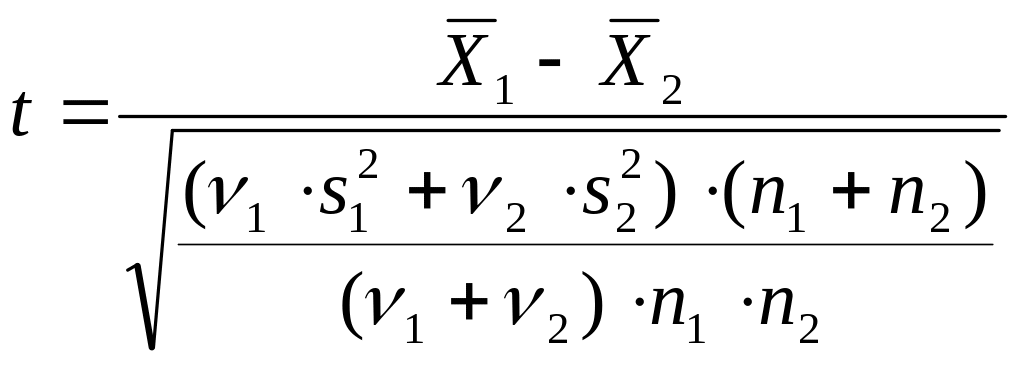, (3.10)
распределена по закону Стьюдента с числом степеней свободы = 1 + 2 – 2.
Здесь где 1 = n1 - 1 – число степеней свободы для первой выборки; 2 = n2 – 1 – число степеней свободы для второй выборки.
Границы критической области находят по таблицам t-распределения или с помощью компьютерной функции СТЬЮДРАСПОБР. Распределение Стьдента симметрично относительно нуля, поэтому левая и правая границы критической области одинаковы по модулю и противоположны по знаку: -tгр и tгр.
Для примера, представленного в табл. 3.4, получим: 1 = 2 = 20 – 1 = 19; t = –2.51, = 38. При = 0,05 tгр = 2.02.
Значения критерия выходит за левую границу критической области поэтому принимаем гипотезу Н1: генеральные средние различны. При этом среднее генеральной совокупности первой выборки меньше.
Применимость t-критерия Стьюдента
Критерий Стьюдента применим только к выборкам из нормальных совокупностей с одинаковыми генеральными дисперсиями. Если хотя бы одно из условий нарушено, то применимость критерия сомнительна. Требование нормальности генеральной совокупности обычно игнорируют, ссылаясь на центральную предельную теорему. Действительно, разность выборочных средних, стоящая в числителе (3.10), может считаться нормально распределенной при > 30. Но вопрос о равенстве дисперсий проверке не подлежит, и ссылки на то, что «критерий Фишера не обнаружил различий» принимать во внимание нельзя. Тем не менее, t-критерий достаточно широко применяется для обнаружения различий в средних значениях генеральных совокупностей, хотя и без достаточных оснований.
Ниже рассматривается непараметрический критерий который с успехом используют для этих же целей, и который не требует ни нормальности ни равенства дисперсий.
§ 3.8. Непараметрическое сравнение двух выборок: критерий Манна-Уитни
Непараметрические критерии предназначены для обнаружения различий в законах распределения двух генеральных совокупностей. Критерии, которые чувствительны к различиям генеральных срекдних, называют критериями сдвига. Критерии, которые чувствительны к различиям генеральных дисперсий, называют критериями масштаба. Критерий Манна-Уитни относится к критериям сдвига и используется для обнаружения различий в средних значениях двух генеральных совокупности, выборки из которых представлены в ранговой шкале. Измеренные признаки распологаются на этой шкале в порядке возрастания, а затем нумеруются целыми числами 1, 2, ...Эти числа и называются рангами. Равным величинам присваивают одинаковые ранги. Значение имеет не сама величина признака, а лишь порядковое место, который она занимает среди других величин. В таблице 3.5. первая группа из таблицы 3.4 представлена в развернутом виде (строка 1), подвергнута ранжированию (стока 2), а затем ранги одинаковых величин, заменены на среднеарифметическими значениями. Например элементы 4 и 4, стоящие в первой строке, получили ранги 2 и 3, которые затем заменены на одинаковые значения 2,5.
Таблица 3.5
3 |
4 |
4 |
5 |
5 |
5 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
7 |
7 |
7 |
7 |
8 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
1 |
2,5 |
2,5 |
5 |
5 |
5 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
15,5 |
15,5 |
15,5 |
15,5 |
18,5 |
18,5 |
20 |