5. Создание графика

MATLAB имеет широкие возможности для графического изображения векторов и матриц, а также для создания комментариев и печати графиков. Приведем описание несколько важных графических функций. 

Функция plot имеет различные формы, связанные с входными параметрами, например plot(y) создает кусочно-линейный график зависимости элементов y от их индексов. Если в качестве аргументов заданы два вектора, то plot(x,y) создаст график зависимости y от x.

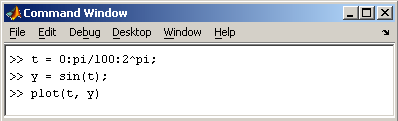
Рисунок 1.2. Пример команд для построения графика функции sin в интервале от 0 до 2

Программа построила график зависимости, который отображается в окне Рисунок 1.3.

Рисунок 1.3. График функции sin в интервале от 0 до 2

MATLAB автоматически присваивает каждому графику свой цвет (исключая случаи, когда это делает пользователь), что позволяет различать наборы данных.

Команда hold on позволяет добавлять кривые на существующий график. Функция subplot позволяет выводить множество графиков в одном окне

Рисунок 1.4. Пример использования функции subplot.

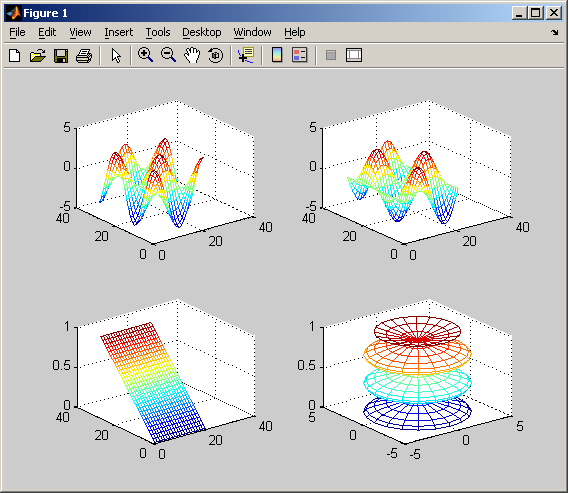
Рисунок 1.15. Результат использования функции subplot.

6. Печать графиков

Пункт Print в меню File и команда print печатают графику MATLAB. Меню Print вызывает диалоговое окно, которое позволяет выбирать общие стандартные варианты печати. Команда print обеспечивает большую гибкость при выводе выходных данных и позволяет контролировать печать из М-файлов. Результат может быть послан прямо на принтер, выбранный по умолчанию, или сохранен в заданном файле.

3. Лабораторная работа № 1

Цель работы: освоить операции матричных вычислений средствами универсальной системы MATLAB.

1. Базовые сведения

Матрицей называется прямоугольная таблица чисел, которая обозначается заглавной полужирной буквой, к примеру (A), а ее элементы — соответствующими строчными буквами с индексами, т.е. a_ij. Первый индекс нумерует строки, а второй — столбцы.

Матрицы можно умножать на числа. При этом каждый элемент умножается на это число. Две матрицы одинаковой размерности можно поэлементно складывать и вычитать. В результате умножения на число и сложения получается матрица той же размерности.

Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O. Очевидно, что A+O = A, A−A = O и 0A = O.

Матрицу можно транспонировать. При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A' или индексом A^Т. Таким образом, если A = {a_ij, i = ,..., m; j = 1,...,n}, то A^T = {a_ji, j = 1,...,n; i = 1,..., m}.

Очевидно, что (A^T)^T = A, (A+B)^T = A^T+B^T.

Матрицы можно перемножать, но только в том случае, когда они имеют соответствующие размерности. Произведением матрицы A, размерностью m×l, и матрицы B, размерностью l×n, называется матрица C, размерностью m×n. Правило скалярного перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C, стоящий на пересечении i-ой строки и j-ого столбца (c_ij) надо поэлементно перемножить i-ую строку первой матрицы A на j-ый столбец второй матрицы B и сложить все результаты. Произведение матриц зависит от порядка их умножения, т.е. AB ≠ BA, хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = (AB)C = A(BC). Кроме того, оно еще и дистрибутивно, т.е. A(B+C) = AB+AC. Очевидно, что AO = O.

Если число столбцов матрицы равно числу ее строк (m = n =k), то такая матрица называется квадратной. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами. Единичной матрицей (обозначается I, а иногда E) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1. Очевидно AI = IA = A. Матрица называется диагональной, если все ее элементы, кроме диагональных (a_ii) равны нулю. Матрица A называется верхней треугольной, если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a_ij = 0, при i>j. Аналогично определяется и нижняя треугольная матрица. Матрица A называется симметричной, если A^T = A. Иными словами a_ij = a_ji. Матрица A называется ортогональной, если A^TA = AA^T = I. Матрица называется нормальной если A^TA = AA^T.

Следом квадратной матрицы A (обозначается Tr(A) или Sp(A)) называется сумма ее диагональных элементов,

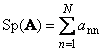
Очевидно, что

Sp(α A) = α Sp(A) и

Sp(A+B) = Sp(A)+ Sp(B).

Можно показать, что

Sp(A) = Sp(A^T), Sp(I) = N,

а также, что

Sp(AB) = Sp(BA).

Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det(A)). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда

Для матрицы (3×3) определитель будет равен

.

Справедливы следующие свойства:

det(I) = 1, det(A) = det(A^Т),

det(AB) = det(A)det(B).

Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A^-1, определяемую условиями

  AA⁻¹ = A⁻¹A = I.

Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является

det(A) ≠ 0 или rank(A) = N.

Если матрицы A и B невырождены, то 

(AB)⁻¹ = B⁻¹A⁻¹.

Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A⁺, что AA⁺A = A.

Псевдобратная матрица — не единственная и ее вид зависит от способа построения. К примеру, если матрица А является прямоугольной, то можно воспользоваться условиями Мура-Пенроуза: если число столбцов меньше числа строк, то псевдообратная матрица A⁺представляется, как A⁺=(A^ТA)⁻¹A^Т.

Если матрица состоит только из одного столбца (n = 1), то такой объект называется вектором. Точнее говоря, вектором-столбцом. Можно рассматривать и матрицы, состоящие из одной строки. Этот объект также является вектором, но вектором-строкой.

Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина

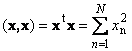
определяет квадрат длины вектора x. Для обозначения длины (называемой также нормой вектора) используется обозначение

Вектор единичной длины (||x|| = 1) называется нормированным. Ненулевой вектор (x ≠ 0) можно нормировать, разделив его на длину, т.е. x = ||x|| (x/||x||) = ||x|| e. Здесь e = x/||x|| — нормированный вектор. Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.

Собственные значения и собственные векторы

Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A, если 

Av = λv, 

где число λ называется собственным значением матрицы A. Таким образом, преобразование, которое выполняет матрица A над вектором v, сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и αv — тоже собственный вектор. У матрицы A , размерности (n×n) не может быть больше чем n собственных значений. Они удовлетворяют характеристическому уравнению det(A − λI) = 0, являющемуся алгебраическим уравнением n-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

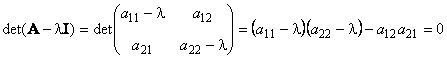
Набор собственных значений λ₁,..., λ_n матрицы A называется спектром A.

Спектр обладает разнообразными свойствами. В частности

 det(A) = λ₁×...× λ_n,                Sp(A) = λ₁+...+ λ_n.

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (A^T = A), то ее собственные значения вещественны.