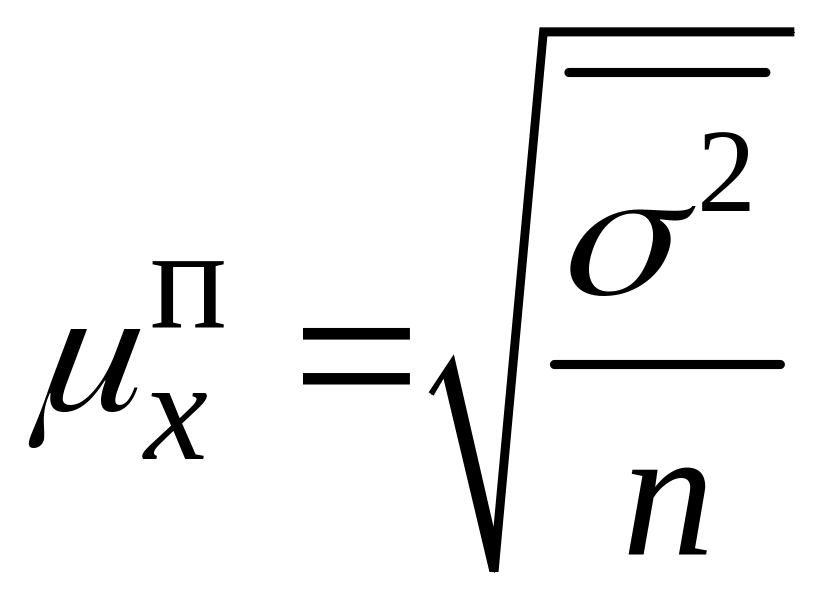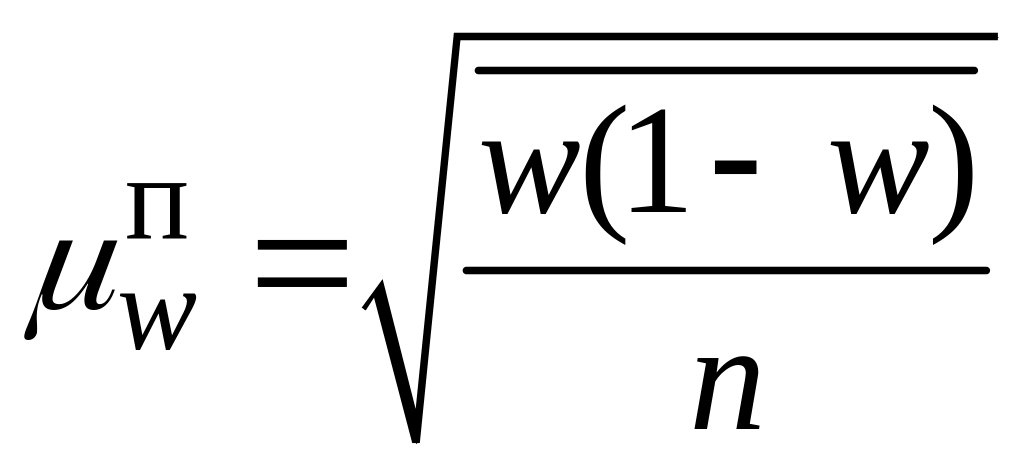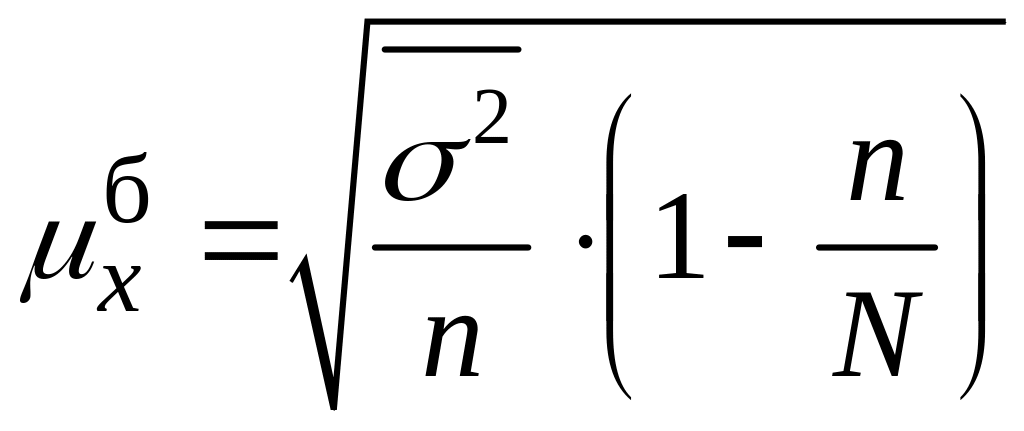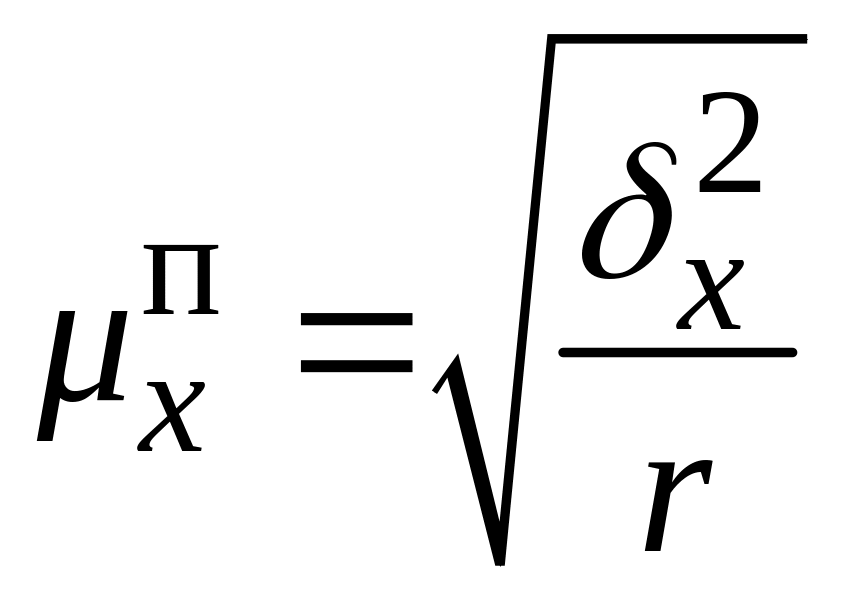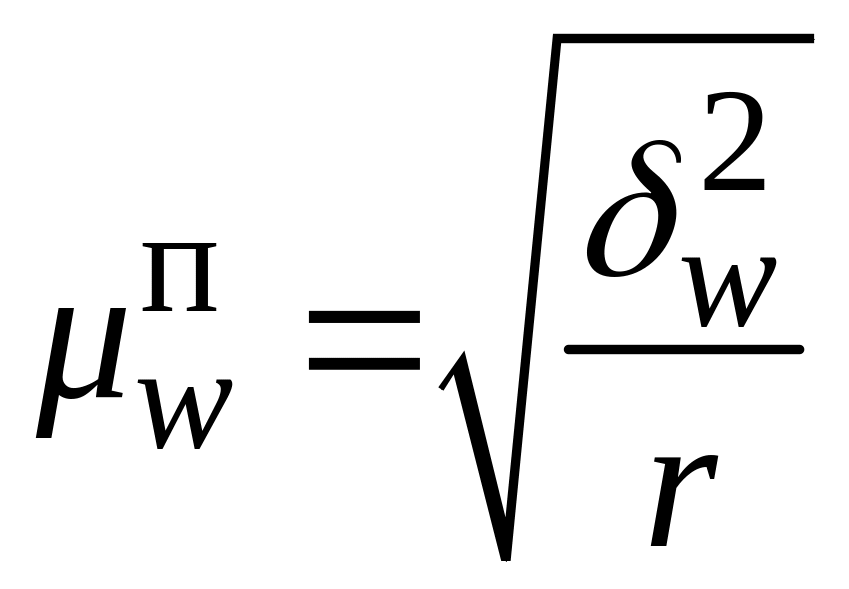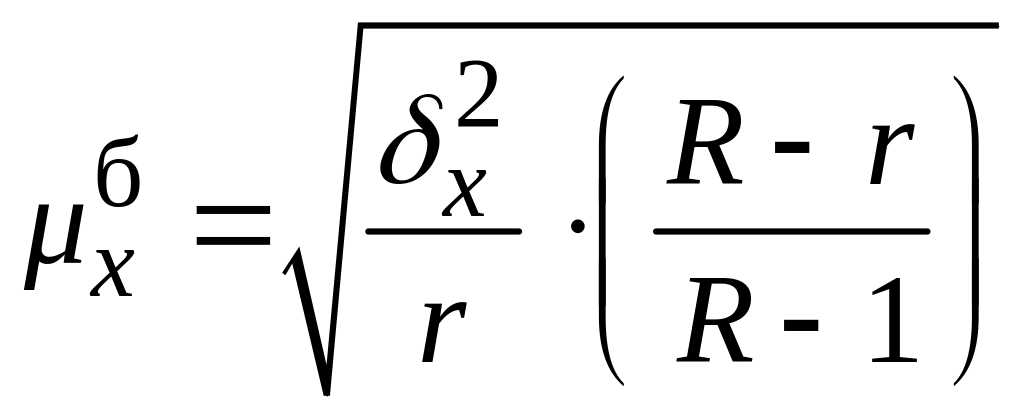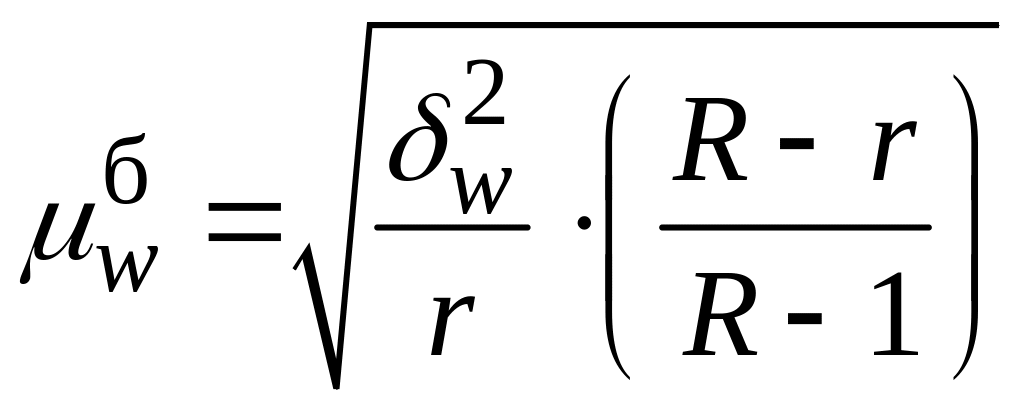- •Література ………………………………………………………………..102 вступ
- •1. Відносні величини
- •Завдання № 1
- •2. Побудова рядів розподілу. Інтервальні та дискретні варіаційні ряди
- •Завдання № 2
- •3. Середні величини
- •Завдання № 3
- •4. Показники варіації варіаційних ознак
- •Деякі абсолютні показники варіації
- •Завдання № 4
- •5. Вибіркове спостереження
- •Середні помилки при простому випадковому і механічному відборі
- •Середні помилки при типовому відборі
- •Середні помилки при серійному відборі
- •Мінімально необхідні обсяги вибірки
- •Завдання № 5
- •6. Статистичне вивчення взаємозв’язків між ознаками
- •Розрахункова таблиця для обчислення параметрів рівнянь регресії
- •Динаміка кількості справ, розглянутих у суді, та тих, рішення за якими лишилися незмінними
- •Завдання № 6
- •7. Ряди динаміки
- •Завдання № 7
- •8. Індекси
- •Завдання № 8
- •Література
- •49044, М. Дніпропетровськ, вул. Рогальова, 8.
Середні помилки при типовому відборі
Схема відбору |
Параметр, що оцінюється |
|
Середня |
Частка p |
|
Повторна |
|
|
Безповторна |
|
|
Позначення:
![]() –
середня з групових дисперсій;
–
середня з групових дисперсій;
![]() – частка варіант у вибірці, що задовольняють
задану умову;
– частка варіант у вибірці, що задовольняють
задану умову;
 – середня з групових дисперсій для
частки,
– середня з групових дисперсій для
частки,
![]() – частка варіант у k-й
групі, що задовольняють дану умову,
– частка варіант у k-й
групі, що задовольняють дану умову,
![]() – частота k-ї
групи.
– частота k-ї
групи.
Приклад 5.2. З метою вивчення доходів населення за трьома районами області проведено 2 %-й безповторний типовий відбір, результати якого наведено в таблиці:
Район |
Кількість населення, чол. |
Досліджено, чол.
|
Щомісячний дохід у розрахунку на 1 людину |
|
середній, тис. грн., |
групова дисперсія,
|
|||
I II III |
120 000 170 000 90 000 |
2400 3400 1800 |
2,9 2,5 2,7 |
1,3 1,1 1,6 |
Разом |
380 000 |
7600 |
Х |
Х |
Встановити межі середньодушового доходу населення області в цілому з імовірністю 0,997.
Розв’язування. Обчислимо вибіркові середню щомісячного доходу однієї особи:
 тис. грн.
тис. грн.
та середню з групових дисперсій
![]() ,
скориставшись формулою (4.3):
,
скориставшись формулою (4.3):
 .
.
За таблицями функції Ф(t) з умови Ф(tγ )=γ знаходимо коефіцієнт довіри t0,997 =2,96. Визначимо середню і граничну помилки вибірки:
 ,
,
![]() .
.
У результаті одержуємо інтервальну оцінку середньодушового доходу населення області:
![]() ,
,
або
![]() тис.
грн.
тис.
грн.
Отже, з імовірністю 0,95 можна стверджувати, що середньодушовий щомісячний дохід населення області знаходиться в межах від 2,59 до 2,71 тис. грн.
При серійному відборі з рівними за обягами серіями середня помилка вибірки обчислюється за формулами, які подано у табл. 5.3.
Таблиця 5.3
Середні помилки при серійному відборі
Схема відбору |
Параметр, що оцінюється |
|
Середня |
Частка p |
|
Повторна |
|
|
Безповторна |
|
|
Позначення:
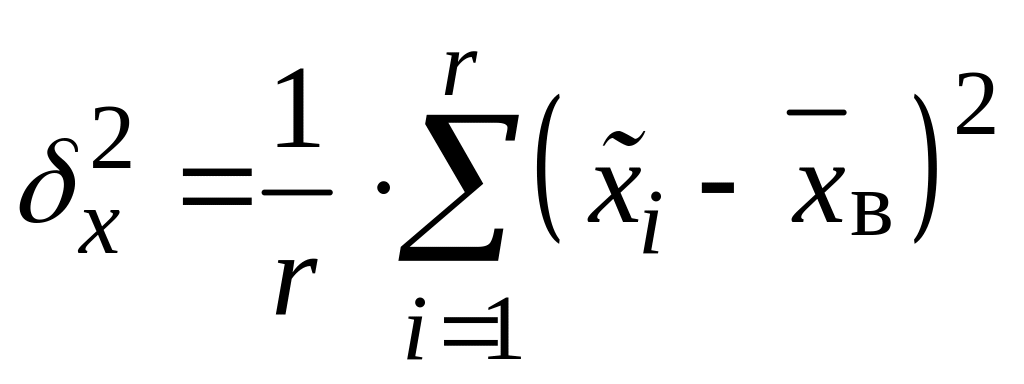 – міжсерійна дисперсія при рівновеликих
серіях,
– міжсерійна дисперсія при рівновеликих
серіях,
![]() – середнє значення ознаки в i-й
серії;
– загальна середня ознаки для всієї
вибірки;
– частка варіант у вибірці, що задовольняють
задану умову;
– середнє значення ознаки в i-й
серії;
– загальна середня ознаки для всієї
вибірки;
– частка варіант у вибірці, що задовольняють
задану умову;
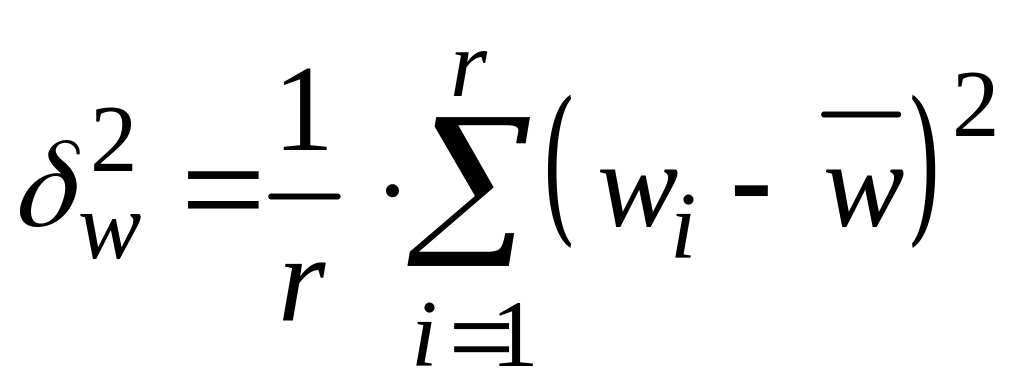 – міжсерійна дисперсія для частки
;
– міжсерійна дисперсія для частки
;
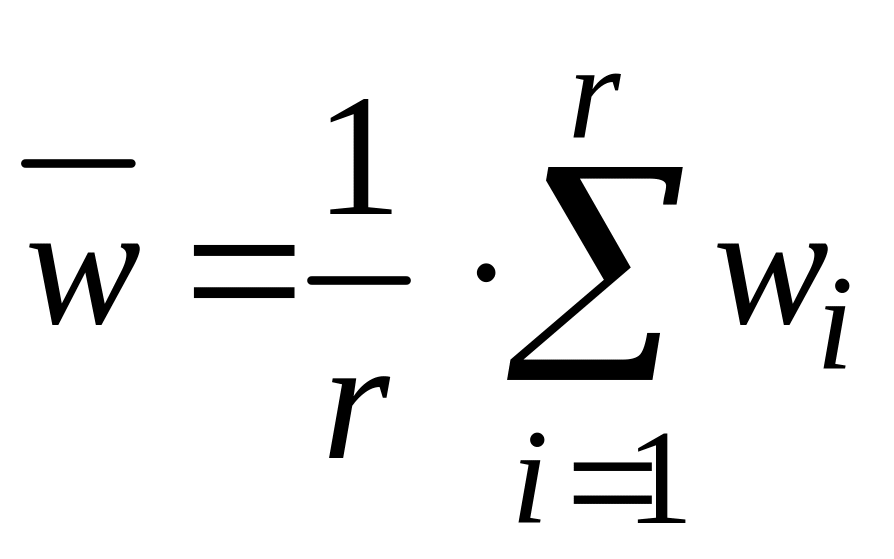 – середня частка для вибраних серій;
– частка варіант у i-й
серії, що задовольняють дану умову; r
– число відібраних серій; R
– загальне число серій у генеральній
сукупності.
– середня частка для вибраних серій;
– частка варіант у i-й
серії, що задовольняють дану умову; r
– число відібраних серій; R
– загальне число серій у генеральній
сукупності.
Приклад 5.3. З метою контролю якості партії мінеральної води, що упакована у 50 ящиків по 20 пляшок об’ємом 1 л у кожній, було проведено 10 %-не серійне безповторне вибіркове спостереження. За 5 ящиками, що потрапили у вибірку, середнє відхилення наповненості пляшок від норми відповідно становило 9, 11, 12, 8 та 14 мл. З імовірністю 0,954 встановити довірчі межі середнього відхилення наповненості пляшок від норми у всій партії в цілому.
Розв’язування. Обчислимо середнє відхилення наповненості пляшок від норми у всій вибірковій сукупності:
![]() мл.
мл.
Визначимо величину міжгрупової дисперсії:
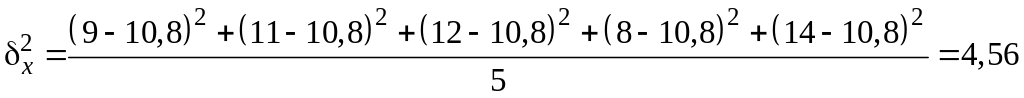 .
.
Для заданої ймовірності =0,954 за таблицею значень функції Ф(t) знаходимо коефіцієнт довіри t0,954 =2. Тоді гранична похибка вибірки становить:
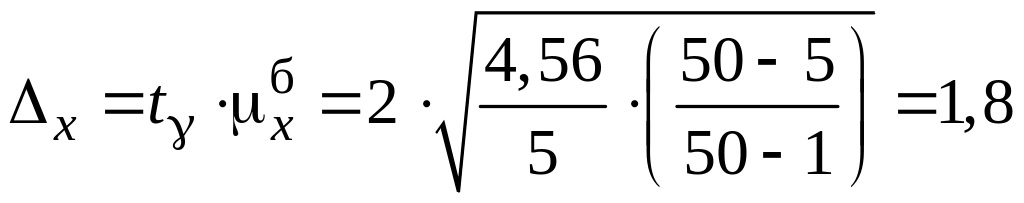 мл.
мл.
Отримаємо довірчі межі середнього відхилення наповненості пляшок від норми:
![]() ,
,
або
![]() мм.
мм.
Отже, з імовірністю 0,954 можна стверджувати, що середнє відхилення наповненості пляшок від норми у всій партії в цілому знаходиться в межах від 9,0 до 12,6 мл.
Під
час планування вибіркового спостереження
іноді виникає необхідність хоча б
наближено визначити мінімально необхідний
обсяг вибірки, який забезпечував би із
заданою надійністю задану точність
інтервальних оцінок параметрів
генеральної сукупності. Цей обсяг
визначається з такої умови: фактична
гранична помилка інтервальної оцінки
не повинна перевищувати задану максимально
допустиму помилку
![]() із заданою надійністю γ.
Наприклад, при повторному відборі для
оцінки генеральної середньої
:
із заданою надійністю γ.
Наприклад, при повторному відборі для
оцінки генеральної середньої
:
![]() ,
звідки
,
звідки
![]() Аналогічно можна одержати величини
мінімально необхідних обсягів вибірки
для інших випадків (див. табл. 5.4).
Аналогічно можна одержати величини
мінімально необхідних обсягів вибірки
для інших випадків (див. табл. 5.4).
Таблиця 5.4