3.7. Метод архитекторов

Пример 3.8

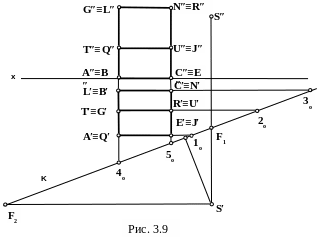
Методом архитекторов построить перспективу архитектурного элемента, заданного ортогональными проекциями (рис.3.9).

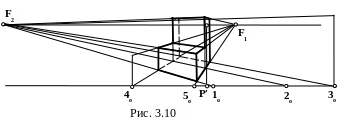
Решение (рис 3.10)

Метод архитекторов (иначе называемый методом точек схода) используется в тех случаях, когда у объекта много параллельных линий.

При построении перспективного изображения архитектурного элемента наиболее удобным считается случай, когда картинная плоскость составляет с гранями объекта угол равный 20^о-30^о. Для того, чтобы объект попадал в конус наилучшего зрения (≈28^о), расстояние от наблюдателя до картины должно быть равно приблизительно удвоенному габариту объекта. А высота стояния – 2/3 высоты объекта.

Для построения перспективного изображения следует (рис. 3.10):

1. Определить положение главной точки картины P. Для этого нужно на горизонтальной проекции опустить перпендикуляр на горизонтальный след картинной плоскости K.

2. Провести через точку зрения S прямые SF₁ и SF₂, параллельные основным конструктивным линиям объекта. Точки пересечения их горизонтальных проекций с горизонтальным следом картинной плоскости укажут положение точек схода F₁ и F₂ пучков параллельных прямых.

3. Положение любой прямой в пространстве вполне определяется положением двух точек ей принадлежащих. Второй точкой, определяющей прямую, может быть ее картинный след. Картинные следы 1_о, 2_о, 3_о соответствуют прямым AE, BC, GR, LN, TU с точкой схода F₁. Картинные следы 4_о, 5_о соответствуют прямым AB, CE, GL, NR с точкой схода F₂.

4. Высота разных частей объекта строится по масштабу высоты.

Задание 3.51

Методом архитекторов построить перспективу плоской пластины, заданной ортогональными проекциями.

2

Задание 3.52

Методом архитекторов построить перспективу геометрического объекта, заданного ортогональными проекциями.

3.8. Примеры решения метрических и позиционных задач

Как правило, на перспективных изображениях метрические задачи решаются редко. Это связано со сложностью и громоздкостью построений. Проще выполнить такие построения в ортогональных проекциях, а затем использовать полученные результаты при построении перспективы объекта. Однако решение подобных задач непосредственно на перспективных изображениях вполне возможно.

Пример 3.9

Определить действительную величину отрезка AB, заданного перспективой и перспективой основания.

Решение (рис. 3.11)

1. Пользуясь перспективным делительным масштабом определить действительную величину основания отрезка AB. Для этого надо построить точку измерения M и из нее провести измерительные лучи 1₀M и 2₀M через перспективы основания точек A′_K и B′_K. Отрезок 1₀2₀ на основании картины будет соответствовать действительной величине основания отрезка AB.

2. По масштабу высоты, пользуясь в качестве точки измерения главной точкой картины P, определить высоту точек A и B, т. е. расстояние от точек до предметной плоскости (Z_A и Z_B).

3. Построить прямоугольный треугольник действительной величины, взяв за один катет действительную величину основания отрезка 1₀2₀, а за другой – разность высот для точек A и B (Z_A – Z_B = ΔZ). Гипотенуза этого треугольника будет равна действительной величине отрезка AB.

Пример 3.10

На прямой m отложить отрезок AB, длина которого равна четырем условным метрам.

Решение (рис 3.12)

1. Ограничим прямую m произвольной точкой C. Определим действительную величину отрезка AC. Для этого, воспользовавшись перспективным делительным масштабом, определим действительную величину основания отрезка AC. И с помощью масштаба высоты определим высоту точек A и C. Зная действительную величину основания отрезка и разность высот точек A и C, построим прямоугольный треугольник. Гипотенуза этого треугольника будет равна действительной величине отрезка AC.

2. Отложим на гипотенузе отрезок, равный действительной величине AB (4 условных метра), и, построив прямоугольный треугольник, подобный данному, найдем положение картинного следа 5₀ измерительного луча М₁5. Точка пересечения этого луча с перспективой основания прямой m определит положение перспективы основания точки B′_K. На линии проекционной связи и на перспективе прямой построим перспективу точки B_K.

Пример 3.11

Определить расстояние от точки C до прямой AB, если прямая AB параллельна предметной плоскости.

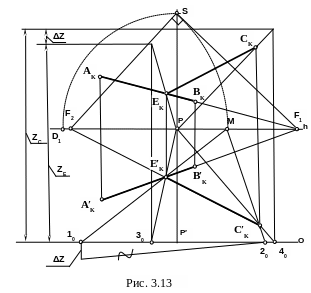
Решение (рис. 3.13)

1. Для того чтобы найти расстояние от точки до прямой, нужно из точки опустить на эту прямую перпендикуляр. По теореме о проецировании прямого угла для ортогонального проецирования, если одна из сторон прямого угла параллельна плоскости проекций (например, горизонтальной), то на эту плоскость угол проецируется без искажения. Таким образом, если угол CEA – прямой, а сторона EA параллельна предметной плоскости, то и основание этого угла C′E′A′ также будет прямым углом.

2. В совмещенной плоскости горизонта через совмещенную точку зрения S и точку F₁ – точку схода пучка прямых, параллельных AB, проведем прямую SF₁, параллельную прямой AB.

3. В совмещенной плоскости горизонта проведем прямую SF₂ перпендикулярно прямой SF₁ и параллельно CE. Полученная точка F₂, будет являться точкой схода всех прямых, параллельных искомому перпендикуляру CE.

4. Через точки C′_K и F₂ проведем перспективу основания перпендикуляра, получив точку E′_K – перспективу основания перпендикуляра CE.

5. На линии проекционной связи и на перспективе прямой A_KB_K построим перспективу точки E_K.

6. Так же, как в предыдущем примере, определим действительную величину отрезка CE.

Пример 3.12

Определить расстояние между скрещивающимися прямыми AB и CE

Решение (рис. 3.14)

1. Поскольку прямая AB перпендикулярна предметной плоскости, положение перспективы основания точки G′_K основания перпендикуляра между заданными прямыми определено вполне. G′_K ≡ A′_K ≡ B′_K.

2. Перпендикуляр GN, опущенный из точки G на прямую CE, перпендикулярен прямой AB и, следовательно, параллелен предметной плоскости. По теореме о проецировании прямого угла для ортогонального проецирования, если одна из сторон прямого угла параллельна плоскости проекций (например, горизонтальной), то на эту плоскость угол проецируется без искажения. Таким образом, если угол GNC – прямой, а сторона GN параллельна предметной плоскости, то и основание этого угла G′N′C′ также будет прямым углом.

3. В совмещенной плоскости горизонта через совмещенную точку зрения S и точку F₂ - точку схода пучка прямых, параллельных CE, проведем прямую SF₂, параллельную прямой CE.

4. В совмещенной плоскости горизонта проведем прямую SF₁ перпендикулярно прямой SF₂ и параллельно GN. Полученная точка F₁, будет являться точкой схода всех прямых, параллельных искомому перпендикуляру GN.

5. Через точки C′_K и F₁ проведем перспективу основания перпендикуляра, получив точку N′_K – перспективу основания перпендикуляра GN.

6. На линии проекционной связи и на перспективе прямой C_KE_K построим перспективу точки N_K.

7. Так как отрезок GN параллелен предметной плоскости, его перспектива будет проходить через точки F₁ и N_K. На пересечении прямой F₁N_K и перспективы прямой A_KB_K определится положение перспективы точки G_K.

8. Поскольку отрезок GN параллелен предметной плоскости, и, следовательно, величина его основания равна действительной величине отрезка, определим действительную величину основания GN с помощью перспективного делительного масштаба.

Пример 3.13

Определить расстояние от точки C до прямой AB, если прямая AB параллельна картинной плоскости.

Решение (рис. 3.15)

1. В ортогональных проекциях методом замены плоскостей проекций проведем новую вспомогательную фронтальную плоскость проекций, параллельную прямой AB и совпадающую с картинной плоскостью. При этом новая ось x₁ совпадет с основанием картины OO.

2. Построим проекции точек A, B и C на эту плоскость. Для этого через точки A, B и С проведем проецирующие лучи, перпендикулярные картине PA_x1, PB_x1 и PC_x1.

3. На линиях проекционных связей и на перспективе проецирующих лучей PA_K, PB_K и PC_K, перпендикулярных картине, определим положение новых фронтальных проекций точек A″₁, B″₁ и C″₁ .

4. Поскольку прямая AB параллельна новой фронтальной плоскости проекций V₁, то по теореме о проецировании прямого угла прямой угол, образованный прямой AB и перпендикуляром CN, будет проецироваться на эту плоскость без искажения. При этом определится положение точек N″₁ - основания перпендикуляра и N_x1.

5. Через точку N проведем проецирующий луч PN_x1, перпендикулярный картине. На пересечении этого луча с перспективой основания прямой A′_KB′_K построим перспективу основания точки N′_K – основания перпендикуляра.

6. На линии проекционной связи и на перспективе прямой AB построим перспективу точки N_K.

7. Проверим себя: если построение проведено верно, проецирующий луч PN″ должен пройти через перспективу точки N_K.

8. Определим действительную величину отрезка CN. Для этого с помощью перспективного делительного масштаба определим действительную величину основания отрезка CN (она равна величине отрезка 1₀ 2₀). Затем с помощью масштаба высоты найдем разность высот точек C и N. На основании полученных данных построим прямоугольный треугольник действительной величины, гипотенуза которого будет равна действительной величине отрезка CN.

Пример 3.14

Через прямую AB провести плоскость Q, перпендикулярную предметной плоскости. Построить линии ее пересечения с предметной плоскостью (предметный след) и с картинной плоскостью (картинный след).

Решение (рис. 3.16)

1. Две плоскости перпендикулярны, если одна из них содержит перпендикуляр к другой плоскости. Для того, чтобы через прямую AB провести плоскость перпендикулярно плоскости H, через любую точку прямой (например, через точку A) проведем прямую AC, перпендикулярную предметной плоскости. Перспектива основания такой прямой – точка (A′_K ≡ C′_K). Перспектива A_K C_K перпендикулярна линии горизонта hh.

2. Для того чтобы построить предметный след плоскости нужно построить предметные следы двух прямых этой плоскости принадлежащих. Точка E′_K ≡ E_K пересечения перспективы прямой A_KB_K с перспективой основания A′_KB′_K – предметный след прямой AB. Точка A′_K ≡ C′_K – предметный след прямой AC. Таким образом, перспектива предметного следа Q_H, будет совпадать с перспективой основания предметного следа плоскости, и проходить через перспективу основания любой прямой, принадлежащей этой плоскости. Следовательно, можно говорить о собирательном свойстве предметного следа плоскости, перпендикулярной плоскости H. (Поскольку перспектива предметного следа плоскости Q совпадает с его перспективой основания (Q_KH≡Q′_KH), то, для того чтобы не загромождать чертеж, обозначим положение перспективы и перспективы основания предметного следа – Q_H).

3. Картинный след такой плоскости совпадет с собственной перспективой (Q_K ≡ Q_KK) и будет перпендикулярен основанию картины OO, проходя через точку 1₀ – перспективу основания картинного следа любой прямой, принадлежащей плоскости Q, что является отличительным признаком плоскости, перпендикулярной плоскости H. Перспектива основания картинного следа будет представлять собой точку, совпадающую с точкой 1 (Q′_KK′≡1₀). Так как положение перспективы предметного следа Q_KH и перспективы его основания Q′_KH вполне определено, то для того чтобы не загромождать чертеж, будем обозначать только перспективу картинного следа – Q_K.

Пример 3.15

Через прямую AB провести плоскость Q перпендикулярно картинной плоскости. Построить линии ее пересечения с предметной плоскостью (предметный след) и с картинной плоскостью (картинный след).

Решение (рис. 3.17)

1. Две плоскости перпендикулярны, если одна из них содержит перпендикуляр к другой плоскости. Для того, чтобы через прямую AB провести плоскость перпендикулярно плоскости K, через любую точку прямой (например, через точку A) проведем прямую A1, перпендикулярную картинной плоскости.

2. Для того чтобы построить картинный след плоскости найдем картинные следы двух прямых этой плоскости принадлежащих. Например, прямой AB и A1. Картинный след прямой A1 – точка 1. Картинный след прямой AB – точка 2. Перспектива основания картинного следа совпадет с основанием картины. Перспектива картинного следа Q_K пройдет через перспективы точек 1_K и 2_K.

3. Для того, чтобы построить предметный след плоскости Q_H найдем предметные следы двух прямых, принадлежащих плоскости. Поскольку предметный след прямой AB не попадает в рамку картины, проведем в плоскости две любые другие прямые. Например, прямую A3 (предметный след – точка 4), и прямую B5 (предметный след – точка 6). Перспектива предметного следа Q_H совпадает с собственной перспективой основания и проходит через точки 4 и 6. Поскольку предметный след Q_H перпендикулярен основанию картины, то его перспектива обязательно проходит через главную точку картины P, что является отличительным признаком плоскости перпендикулярной к картине.

Пример 3.16

Построить линии пересечения плоскости, общего положения Q, заданной прямыми AB и CE, с плоскостью H (предметный след плоскости Q) и с плоскостью K (картинный след плоскости Q).

Решение (рис. 3.18)

1. Положение любой прямой в пространстве (в том числе и следа плоскости) определяется положением двух точек этой плоскости принадлежащих. Для того, чтобы построить предметный след плоскости Q_H, построим предметные следы двух прямых этой плоскости. Например, прямой AB (предметный след – точка 1_K ≡ 1′_K′) и прямой BC (предметный след – точка 2_K ≡ 2′_K).

2. Для того, чтобы построить картинный след плоскости Q_K, построим картинные следы двух прямых этой плоскости. Например, прямой AB (картинный след – точка 3) и прямой C4 (картинный след – точка 6).

3. Проверка: поскольку плоскость Q пересекает основание картины в некоторой точке Q₀ (точка схода следов), точка пересечения предметного Q_H и картинного Q_K следов должна находиться на основании картины OO.

Пример 3.17

В плоскости Q, заданной треугольником ABC, провести прямую параллельную предметной плоскости и прямую параллельную картинной плоскости.

Решение (рис. 3.19)

1. Построим предметный след плоскости Q_H. Для этого построим предметные следы двух прямых, принадлежащих плоскости. Например, точку 2 (предметный след прямой AB) и точку 3 (предметный след прямой СB. Зная положение предметного следа Q_H, определим положение бесконечно удаленной точки этого следа F. Проведем произвольную прямую, принадлежащую плоскости, имеющую эту же бесконечно удаленную точку, например, прямую BF. Положение перспективы этой прямой определится положением точки 1, принадлежащей прямой BF и прямой AC.

2. У прямой параллельной картине, перспектива основания параллельна основанию картины. Проведем произвольную прямую, перспектива основания которой параллельна основанию картины (например, прямую C4). Положение перспективы такой прямой определяется положением перспектив двух ее точек, например точек С и 4.

Пример 3.18

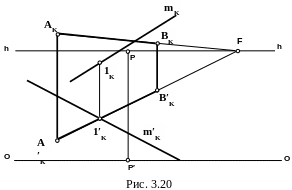
Определить место попадания светового луча m на вертикальный экран. (Построить точку пересечения прямой m с вертикальной плоскостью AB).

Решение (рис.3.20)

Поскольку плоскость AB перпендикулярна предметной плоскости, ее предметный след обладает собирательным свойством. Следовательно, перспектива основания точки пересечения 1′_K будет находиться на пересечении перспективы основания прямой m′_K и перспективы основания экрана A′_KB′_K. А перспектива этой точки 1_K будет располагаться на линии проекционной связи и на перспективе прямой m_K.

Пример 3.19

Построить точку пересечения прямой m с плоскостью общего положения ABCE.

Решение (рис. 3.21)

Проведем через прямую m вспомогательную плоскость Q перпендикулярно предметной плоскости. Поскольку предметный след такой плоскости Q_H обладает собирательным свойством, положение перспектив основания точек пересечения прямой AE (1′_K) и прямой BC (2′_K) с вспомогательной плоскостью Q определено вполне. Таким образом, линей пересечения вспомогательной плоскости Q с заданной является линия 1-2. Единственной точкой этой линии, принадлежащей прямой m, будет точка N, которая и является точкой пересечения прямой m и плоскости ABCE.

Пример 3.20

Построить линию пересечения двух плоскостей ABCE и GNTU.

Решение (рис. 3.22)

Положение любой прямой, в том числе и линии пересечения плоскостей, вполне определяется положением двух точек ей принадлежащих.

1. Найдем точку пересечения прямой GN с плоскостью ABCE. Для этого проведем через прямую вспомогательную плоскость Q, перпендикулярную предметной плоскости H. Прямая AE пересекает плоскость Q в точке 1. Прямая BC пересекает плоскость Q в точке 2. Следовательно, линия пересечения плоскостей Q и ABCE – это линия 1-2. Единственной точкой этой прямой, принадлежащей прямой GN, является точка 3.

2. Аналогично найдем точку 6 – пересечения прямой UT с плоскостью ABCE, проведя через прямую UT вспомогательную плоскость R перпендикулярную предметной плоскости H.

3. Линия пересечения плоскостей ABCE и GNTU – это линия 3-6.

4. Определить видимость на перспективе и перспективе основания можно с помощью пар конкурирующих точек 4-7 и 8-9.

Пример 3.21

Определить точку прикрепления оттяжки GL, перпендикулярной к плоскости навеса ABCE, и ее длину. (Определить расстояние от точки G до плоскости общего положения ABCE).

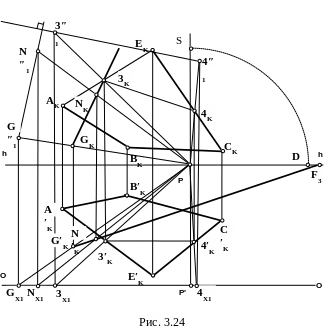
Решение (рис. 3.23 – 3.25)

Прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим плоскости. Решение задачи можно разбить на три этапа:

а) задать направление перпендикуляра,

б) определить точку его пересечения с плоскостью,

в) определить действительную величину перпендикуляра.

1. Зададим направление перспективы основания перпендикуляра GL как прямой, перпендикулярной предметному следу плоскости. (рис.3.23). Порядок проведения прямой, перпендикулярной предметному следу, описан в примере 3.11. Для этого проведем предметный след плоскости ABCE (Q_H) через предметные следы двух прямых, принадлежащих плоскости (точки 1 и 2). Зная бесконечно удаленную точку предметного следа Q_H (точка F₂), через совмещенную точку зрения проведем прямую SF₃, перпендикулярную SF₂. Таким образом определится бесконечно удаленная точка F₃ всех прямых перпендикулярных Q_H.

2. Зададим направление перспективы перпендикуляра GL, как перпендикуляра на картинный след Q_K, или на любую прямую плоскости параллельную картине, например, прямую 3-4) (рис. 3.24). Построение описано в примере 3.13. В ортогональных проекциях методом замены плоскостей проекций проведем новую вспомогательную фронтальную плоскость проекций, параллельную прямой 3-4 и совпадающую с картинной плоскостью. При этом новая ось x₁ совпадет с основанием картины OO.

Построим проекции точек 3, 4 и G на эту плоскость. Для этого через точки 3, 4 и G проведем проецирующие лучи, перпендикулярные картине P3_x1, P4_x1 и PG_x1.

На линиях проекционных связей и на перспективе проецирующих лучей P3_K, P4_K и PG_K перпендикулярных картине определим положение новых фронтальных проекций точек 3″₁ , 4″₁ и G″₁ .

Поскольку прямая AB параллельна новой фронтальной плоскости проекций V₁, то по теореме о проецировании прямого угла, прямой угол, образованный прямой 3-4 и перпендикуляром из точки G, будет проецироваться на эту плоскость без искажения. Ограничим перпендикуляр произвольной точкой N. При этом определится положение точек N″₁ и N_x1.

Через точку N проведем проецирующий луч PN_x1, перпендикулярный картине. На пересечении этого луча с перспективой основания прямой 3′_K4′_K построим перспективу основания точки N′.

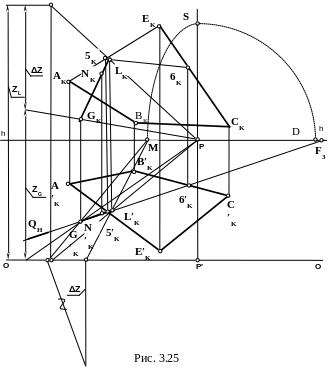
3. Для того чтобы найти точку пересечения прямой GN с плоскостью ABCE, проведем через прямую GN вспомогательную плоскость R, перпендикулярную предметной плоскости H (рис. 3.25). Плоскость R пересекает заданную плоскость по прямой 5-6. Единственная точка прямой 5-6, принадлежащая GN – это точка L, которая и является основанием перпендикуляра, опущенного из точки G на плоскость ABCE. Действительную величину GL найдем, как действительную величину отрезка общего положения (см. пример 3.9).

Пример 3.22

Перпендикулярно наклонному рекламному щиту ABCE установить кронштейны подсветки AL и BN длиной 1 условный метр. ( Восставить к плоскости перпендикуляр заданной длины).

Решение (рис. 3.26, 3.27)

1. Прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим плоскости. Зададим направление перспективы основания перпендикуляра AL как прямой, перпендикулярной предметному следу плоскости. Порядок проведения прямой, перпендикулярной предметному следу описан в примерах 3.11 и 3.21. Нам не нужно строить предметный след плоскости, поскольку щит касается предметной плоскости стороной CE. Так как щит имеет прямоугольную форму, что ясно из задания, нет необходимости находить точку схода прямых, перпендикулярных предметному следу – она совпадает с бесконечно удаленной точкой сторон AE и BC. Таким образом, перспектива основания кронштейна A5 совпадает с перспективой основания стороны A′_KE′_K. А перспектива основания кронштейна B6 совпадает с перспективой основания стороны B′_KC′_K.

2. Так же, как в примерах 3.13 и 3.21, зададим направление перспективы перпендикуляра AL, как перпендикуляра на картинный след Q_K или на любую прямую плоскости, параллельную картине, например, прямую 1-2. В ортогональных проекциях методом замены плоскостей проекций проведем новую вспомогательную фронтальную плоскость проекций, параллельную прямой 1-2 и совпадающую с картинной плоскостью. При этом новая ось x₁ совпадет с основанием картины OO.

Построим проекции точек 1, 2 и A на эту плоскость. Для этого через точки 1, 2 и A проведем проецирующие лучи, перпендикулярные картине P1_x1, P2_x1 и PA_x1.

На линиях проекционных связей и на перспективе проецирующих лучей P3_K, P4_K и PG_K, перпендикулярных картине определим положение новых фронтальных проекций точек 1″₁ , 2″₁ и A″₁ .

Поскольку прямая 1-2 параллельна новой фронтальной плоскости проекций V₁, то по теореме о проецировании прямого угла, прямой угол, образованный прямой 1-2 и перпендикуляром из точки A, будет проецироваться на эту плоскость без искажения. Ограничим перпендикуляр произвольной точкой 3. При этом определится положение точек 3″₁ и 3_x1.

Через точку 3_x1.проведем проецирующий луч P3_x1, перпендикулярный картине. На пересечении этого луча с перспективой основания прямой 3′_KA′_K построим перспективу основания точки 3′_K.

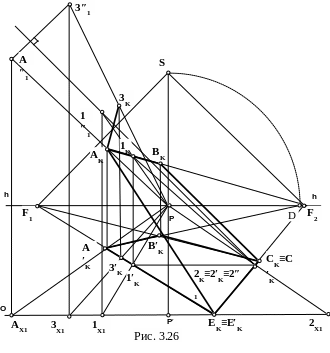
3. Так же, как в примере 3.10, отложим на луче A3 отрезок AL, действительная величина которого равна 1 условному метру (рис. 3.27).

4. Любым удобным методом проведем отрезок BN, параллельный и равный отрезку AL.

Пример 3.23

Определить точки пересечения прямой m с поверхностью пирамиды.

Решение (рис. 3.28)

Проведем через прямую m вспомогательную плоскость Q, перпендикулярную предметной плоскости. Плоскость Q пересечет поверхность пирамиды по линии 1-2-3-4. Точками, общими для прямой m и линии 1-2-3-4, а следовательно, и для поверхности пирамиды, будут точки N и T.

Рис. 3.28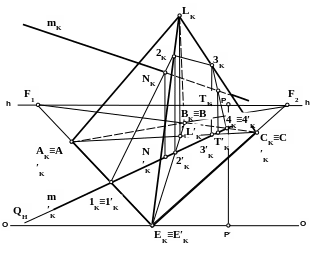

Пример 3.24

Построить перспективное изображение слухового окна. (Построить линию пересечения поверхности прямой призмы с треугольным основанием с плоскостью общего положения ABCE).

Решение. (рис. 3.29)

1. Через ребро 5-6 проведем вспомогательную плоскость Q, перпендикулярную предметной плоскости H. Плоскость Q пересечет заданную плоскости ABCE по линии 7-8. Единственной точкой, принадлежащей ребру 5-6 будет точка 9.

2. Через ребра 5-1 и 5-4 проведем вспомогательную плоскость R (плоскость фронтона слухового окна), перпендикулярную предметной плоскости H. Плоскость R пересечет заданную плоскости ABCE по линии 10-11. Точками, принадлежащей ребрам 5-1 и 5-4, будут соответственно точки 12 и 13.

3. Построим линию пересечения поверхности геометрического тела плоскостью 9-13-12-9.

Пример 3.25

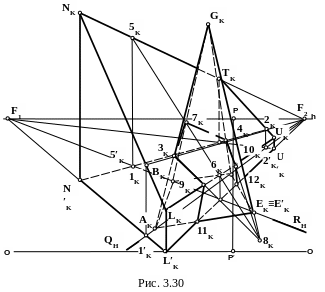
Построить перспективу архитектурного элемента – части стены, ската крыши и четырехгранной башенки (линию пересечения поверхностей прямой усеченной призмы LNTU и четырехгранной пирамиды ABCEG).

Решение (рис. 3.30)

1. Проведем через ребра AG и GC вспомогательную плоскость Q, перпендикулярную предметной плоскости. Линия пересечения плоскости Q с поверхностью призмы – это линия 1′_K-1_K-2_K-2′_K. А точки принадлежащие ребрам AG и GC, – соответственно точки 3 и 4.

2. Проведем через ребра BG и GE вспомогательную плоскость R, перпендикулярную предметной плоскости. Линия пересечения плоскости R с поверхностью призмы – это линия 5′_K5_K6_K6′_K. А точки принадлежащие ребрам AG и GC, – соответственно точки 7 и 8.

3. Точки пересечения ребра U′_KL′_K нижнего основания призмы со сторонами основания пирамиды - точки 9 и 10.

4. Точки пересечения ребра U_KL_K верхнего основания призмы c поверхностью пирамиды – точки 11 и 12.

5. Последовательно соединив точки, построим линию пересечения поверхностей геометрических тел.