3.2. Изображение синусоидальной функции времени вектором и комплексным числом

Для упрощения анализа и расчета цепей синусоидального тока пользуются изображением синусоидальной функции времени, вектором или комплексным числом. Между синусоидальной функцией и ее изображением должно существовать строго однозначное соответствие. При таком методе расчета действия над реальными синусоидальными функциями заменяются действиями над их изображениями- векторами или комплексными числами, так как операции над изображениями производятся легче, чем над реальными величинами. В результате расчета находится изображение искомой величины, а затем с помощью обратного перехода по этому изображению находится искомая величина.

Вектор, соответствующий данной синусоиде, строится для момента времени t = 0. Длина вектора равна действующему значению синусоиды, угол наклона вектора к горизонтальной оси равен начальной фазе синусоиды(положительный угол откладывается против часовой стрелки). Вектор, изображающий данную синусоиду, обозначается большой (прописной) буквой с чертой: Ū, Ī, Ē и называется "вектор напряжения", "вектор тока", "вектор ЭДС". Совокупность векторов, изображающих синусоидальные функции одинаковой частоты с учетом взаимного сдвига по фазе, называется векторной диаграммой. На векторной диаграмме угол между векторами равен сдвигу фаз между соответствующими синусоидальными величинами.

Если вектор расположен на комплексной плоскости, то этому вектору, а следовательно, и синусоидальной функции, можно привести в соответствие комплексное число (рис. 2). Комплексное число, изображающее данную синусоиду, обозначается большой (прописной) буквой с точкой: İ, Ů, Ė и называется "комплекс тока", "комплекс напряжения", "комплекс ЭДС". Предположим, задана синусоида тока:

i= sin(ωt + ψ).

Построим соответствующий вектор на комплексной плоскости (рис.2):

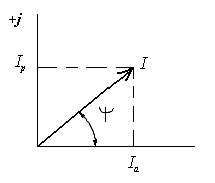
Рис.2. Изображение синусоиды вектором и комплексным числом

Спроектируем вектор на оси ординат: I_a=Icosψ, I_ρ=Isinψ и запишем комплексное число( комплекс тока):

İ= I_a+ jI_ρ= =I(cosψ+jsinψ).

В этом выражении I_a - проекция вектора на действительную ось(+1), равная действительной части комплексного числа, I_ρ - проекция вектора на мнимую ось(+j), равная мнимой части комплексного числа, j= - мнимая единица. Из теории комплексных чисел известно, что I= называется модулем комплексного числа, а ψ = arctgI_ρ/ I_a- его аргументом. Отсюда следует соответствие между комплексным числом и синусоидой: модуль комплексного числа равен действующему значению синусоиды, аргумент ─ ее начальной фазе.

3.3. Законы Кирхгофа для цепи синусоидального тока

Физические процессы в электрических цепях переменного тока отличаются от процессов в цепях постоянного тока. Это в первую очередь связано с влиянием индуктивности и емкости. Переменный ток в индуктивности создает переменное магнитное поле, которое в свою очередь создает ЭДС самоиндукции, влияющую на величину тока; переменное напряжение на емкости приводит к появлению переменного электрического заряда и протеканию тока через емкость. Эти факторы необходимо учитывать при анализе цепей переменного тока. Большое влияние на процессы оказывают также частота тока f и сдвиг фаз между током и напряжением φ. Необходимо также учитывать, какие значения токов и напряжений используются при анализе (мгновенные, действующие и т.д.).

Поскольку законы Кирхгофа справедливы для любого момента времени, то их можно записать для мгновенных значений величин:

∑i_к=0, ∑u_к=∑e_к. ⁽¹⁾

^{Формулировки звучат так: в узле алгебраическая сумма мгновенных значений токов равна нулю; в замкнутом контуре алгебраическая сумма мгновенных значений напряжений на пассивных элементах контура равна алгебраической сумме мгновенных значений ЭДС в этом же контуре. В цепях переменного тока пассивными элементами являются сопротивление проводника R, индуктивность L и емкость C.Через ток эти напряжения можно выразить следующим образом:}

^uR^{=Ri, u}L^{=Ldi/dt, u}C^{= 1/C∫idt . (2)}

^{При подстановке (2) во второе уравнение Кирхгофа (1) получим систему дифференциальных уравнений относительно токов.}

^{В линейных цепях(R,L,C- постоянные величины) при синусоидальной ЭДС все токи и напряжения на участках также изменяются по синусоидальному закону. Поэтому все синусоиды, входящие в уравнения, можно заменить векторами или комплексными числами (п. 3.2) и получить уравнения Кирхгофа для векторов:}

∑Ī_к=0, ∑Ū_к= ∑Ē_к

_{или комплексов:}

∑İ_к=0, ∑Ů_к= ∑Ė_к.

При векторной записи вектор Ūк нельзя выразить через вектор тока Īк, и уравнения приходиться решать при помощи графических построений (векторных диаграмм). Такая форма записи используется при анализе простых цепей. При записи в комплексной форме можно ввести понятие комплексного сопротивления Z, которое определяется как отношение комплекса напряжения к комплексу тока:

Z=Ů/İ = R+jX= ž e^jφ,

где ž- модуль комплексного сопротивления или полное сопротивление;

R- действительная(вещественная) часть комплексного сопротивления или активное сопротивление;

X- мнимая часть комплексного сопротивления или реактивное сопротивление.

Комплексное сопротивление можно найти, если известны параметры цепи R,L,C. Напряжение на пассивном элементе выражается через ток Ůк=Zkİк и уравнения решаются аналитически относительно неизвестных токов. Такая форма записи уравнений применяется при анализе сложных цепей, в том числе с использованием ЭВМ.