Колмаков Ю.Н. Лекции по физике ТулГУ. Основы квантовой теории и атомной физики

3. Квантование момента импульса

91

В качестве выделенной оси выбирают ось z и для

удобства вычислений переходят к сферическим ко-

ординатам (рис.6.3). В этих координатах

ˆ

∂

Lz

= −i

∂ϕ

.

(6.14)

Найдем разрешенные значения Lz , решая задачу

Рис.6.3

(6.7):

dψ(ϕ)

ˆ

Lz ψ(ϕ).

Lz ψ(ϕ) = −i

=

dϕ

Разделяя переменные и интегрируя, получим

∫

dψ

=

i Lz

∫dϕ

и

ln ψ =

i Lz

ϕ+ln A ,

ψ

где ln A – постоянная интегрирования. Тогда

ψ(ϕ)= AeiLzϕ .

(6.15)

Граничным условием в данной задаче будет условие периодичности. При повороте вокруг оси z на угол 2π волновая функция не должна изме-

ниться: ψ(ϕ+ 2π)= ψ(ϕ). В этом случае из формулы (6.15) следует

eiLz 2π = cos(2πL	)+i sin (2πL	)=1.
z	z
=1	=0

Отсюда 2πLz = 2πm , где m – целое число. Найден спектр разрешенных значений проекции момента импульса частицы на выделенную ось z:

Постоянную A в

Lz = m, где

m = 0, ±1, ± 2,...

.

(6.16)

выражении (6.15) находим из

условия нормировки

2π

2π

∫

ψ

2 dϕ =

A

2 ∫ dϕ = 2π

A

2 =1, откуда A = e i α

2π ,

0

0

где α – несущественный фазовый множитель, который обычно приравни-

вают нулю.				ˆ	,	соответст-
				Собственные волновые функции оператора Lz
вующие разрешенным значениям (6.16), имеют вид
				ψm (ϕ) = e i m ϕ 2π .		(6.17)
	Помимо проекции момента импульса на выделенную ось, можно опре-
делить		и	квадрат момента импульса. Оператор этой			величины
ˆ2	ˆ 2	ˆ	2	ˆ 2
L	= L x	+ L y+ L z в сферических координатах запишется как

92								Глава 6. Квантовомеханические операторы
	ˆ	2		2		∂2				∂		1				∂2
	L		= −				2		+ctg θ		+		2				2		.	(6.18)
						∂θ				∂θ		sin		θ ∂ϕ

Легко видеть, что каждое из слагаемых, входящих в это выражение, можно переставить местами с частной производной (∂∂ϕ). Поэтому операторы (6.14) и (6.18) коммутируют и

одновременно можно определить величину момента импульса L (или ее квадрат L2 ) и одну из его проекций, например, проекцию Lz .

Дифференциальное уравнение (6.7) для нахождения разрешенных значений L2

ˆ

2

2

∂2

∂

1

∂2

2

L

ψ(θ,ϕ)= −

2

+ctg θ

+

2

2

ψ(θ,ϕ)= L

ψ(θ,ϕ)

∂θ

∂θ

sin

θ ∂ϕ

функций ψ(θ,ϕ)=

имеет

решение в

виде специальных сферических

= Ylm (θ,ϕ), которые приводятся в математических справочниках и зависят от двух целых чисел l и m. Такие функции будут собственными функциями

и оператора

ˆ2

, и оператора

ˆ

L

Lz :

ˆ2

m

(θ,ϕ)=

2

l (l +1)Yl

m

(θ,ϕ);

ˆ

m

(θ,ϕ)=

m

(θ,ϕ),

(6.19)

L Yl

Lz Yl

m Yl

где целое число l называется орбитальным квантовым числом и может принимать значения l = 0, 1, 2,3,... Как видно из первого уравнения (6.19),

величина момента импульса любой микрочастицы может быть равна только отдельным разрешенным значениям

L = l (l +1)	.	(6.20)

Целое число m называют магнитным квантовым числом. Такое название это квантовое число получило по той причине, что выделенное направление оси z обычно задается направлением внешнего магнитного поля, действующего на заряженные частицы в реальных микросистемах (атомах и т.п.).

Учтем, что L 2z ≤ L2 (проекция вектора не может превышать длины век-

тора), откуда следует m2 < l (l +1) и m ≤ l .

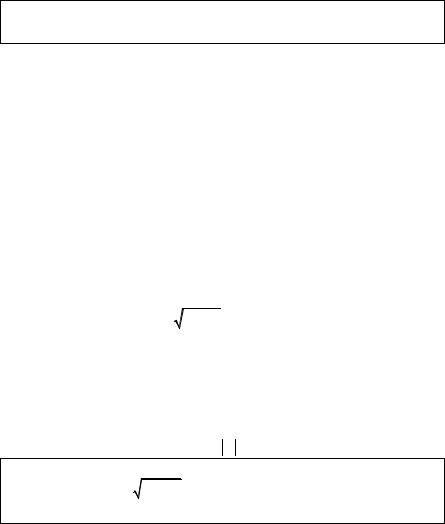
Момент импульса микрочастицы, движущейся в любом внешнем поле, имеет величину L = l (l +1) , l = 0,1, 2,... . Он может иметь только 2l+1 различных значений проекции Lz = m на любую выделенную ось z, где

	3. Квантование магнитного момента		93
	m = 0, ±1, ± 2,..., ±l .
	Пример: в боров-
	ской модели		атома
	(рис.3.6)	плоскость
	электронной орбиты с
	радиусом	rn	должна

быть перпендикулярна сохраняющемуся вектору момента им-

пульса L , величина

которого

Ln = n ,

где n=1, 2, 3,….Этот результат не совпадает с выводом (6.20). Боровская модель неправильно описывает вращение электрона в атоме.

В действительности ориентация вектора L в пространстве не опре-

делена. На рис.6.4 показана возможная ориентация вектора момента импульса электрона в состояниях с квантовыми числами l=1 и l=2. Так как

проекции Lx и Lу определить невозможно, то вектор L изображен на

этом рисунке "размазанным" в конус вокруг оси z. Величины Lz и L при этом определены. Но представить траекторию электрона в виде плоской орбиты, перпендикулярной фиксированному направлению L , нельзя!

3. Квантование магнитного момента

Двигаясь по круговой орбите радиуса r со скоростью v , частица с зарядом q совершает один оборот за время ∆t = 2πrv , и создает эффектив-

ный круговой ток I = ∆q∆t = q v2πr (рис.6.5). Площадь такого тока

S = πr2 , а создаваемый им магнитный момент

pm = IS = qv r			2 .
С учетом направления векторов, указанных на рис.6.5,
движущаяся заряженная частица обладает магнитным
моментом
p =	q	[r, v].	(6.21)
m

	Рис.6.5	2
		Эта формула справедлива не только для круговой, но

и для любой другой траектории частицы. Если учесть, что момент импульса частицы L = [r, p]= m[r, v], то оказывается, что

94	Глава 6. Квантовомеханические операторы

магнитный момент и момент импульса движущейся заряженной частицы связаны соотношением

p =

q

L ,

(6.22)

m 2m

которое называется гиромагнитным отношением.

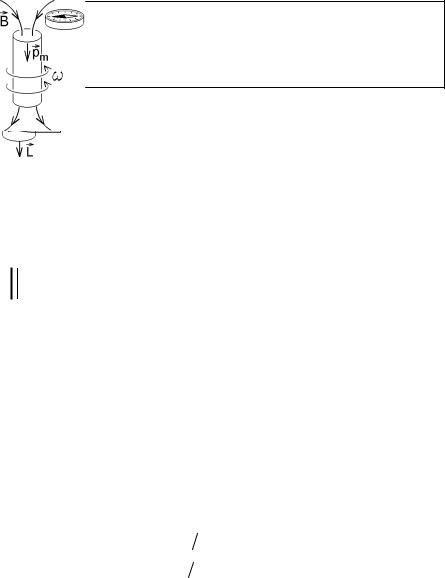
На рис. 6.5 изображено движение положительно заряженной частицы. Заряд электрона q = – e отрицателен, и для электрона с массой me векто-

ры pm и L направлены в противоположные стороны (рис.6.6).

	Намагничивание среды может происходить при появ-
	лении элементарных токов намагничивания, созданных
	движением электронов. При сложении магнитных момен-
Рис.6.6	тов отдельных электронов, согласно формуле (6.22), скла-
	дываются и моменты их импульсов:
	pm = ∑ pmi = −	e	∑Li =−	e	L .
		2me		2me

Гиромагнитное отношение справедливо не только для отдельного электрона, но и для всего намагниченного образца в целом.

Это было проверено в опытах Эйнштейна-де Хааза (1915г.) (рис.6.7). Внутри соленоида с током создавалось

магнитное поле B , которое намагничивало подвешенный металлический цилиндр. При появлении механического момента им-

	пульса L цилиндр начинал вращаться в
	направлении, указанном стрелкой.
	Обратный эффект Барнетта был обна-
	ружен еще в 1909г. Если ферромагнитный
	железный цилиндр привести во вращение
Рис.6.7	(рис.6.8), то он намагничивается и создает	Рис.6.8
	дополнительное магнитное поле B .

Полученная формула (6.22) говорит о том, что магнитный момент заряженной микрочастицы будет квантоваться вместе с ее моментом им-

пульса. Для электрона	ˆ	ˆ
	pm	= −(e 2me )L . Если ввести постоянную
	µБ	= e 2me = 9, 27 10−24 А м2	,	(6.23)

называемую магнетоном Бора (e и m e – заряд и масса электрона), то с учетом формул (6.16) и (6.20) получаем дискретный спектр разрешенных

5. Спин

95

значений величины магнитного момента и его проекции на выделенную ось z для движущегося электрона:

pm = µБ l (l +1) , где l = 0,1, 2,...; pm z = −µБ m, где m = 0, ±1,...±l .(6.24)

Магнетон Бора – это квант магнитного момента. Ориентация вектора pm в пространстве изображается аналогично рис.6.4.

5. Спин

Согласно планетарной модели (рис.3.5) магнитный момент атома должен быть суммой магнитных моментов всех его электронов: pm = ∑ pmi .

Магнитным моментом ядра, в силу формулы (6.22), можно пренебречь, так как масса ядра в тысячи раз больше массы электрона. Попытка измерить pm атома впервые была сделана в опытах Штерна-Герлаха (1921г.),

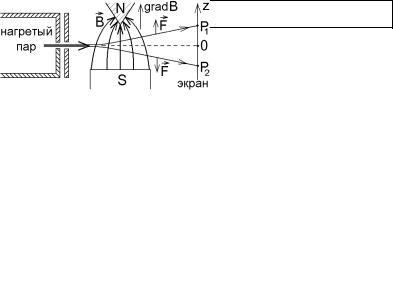
схема которых приведена на рис.6.9.

Узкий пучок атомов испаренного серебра проходил через область неоднородного магнитного поля, градиент которого направлен вдоль оси z. Каждый атом будет крошечным магнитным диполем, энергия которого во внешнем магнитном

Рис.6.9

поле

U = −pm B .

Градиент этой

энергии определяет силу, действующую на атом:

∂

∂Bz .

F

= −grad

U =

p

m x

B

x

+ p

m y

B

y

+ p

B

z

(z)

= p

z

z

∂z

m z

m z ∂z

=const

Отклонение атома вдоль оси z должно быть пропорционально проекции pm z его магнитного момента.

Результат опыта Штерна-Герлаха оказался странным: атомы пучка попадали только в две симметрично расположенные точки P1 и P2 экрана

(рис.6.9), т.е. имели только два разрешенных значения проекции pm z !

Этот результат доказывает, что магнитный момент квантуется (имеет только отдельные разрешенные значения), но противоречит выводу (6.24).

Формула (6.24) предсказывает расщепление пучка атомов на нечетное число 2l +1 пучков (это число разных значений магнитного квантового числа m). Даже если атомы не возбуждены и находятся в состоянии с

96	Глава 6. Квантовомеханические операторы

квантовым числом l=0, весь пучок должен попадать в центральную точку О экрана (рис.6.9).

	Результат опыта Штерна-Герлаха смогла объяснить гипотеза о сущест-
	вовании у микрочастиц момента импульса, не связанного с движением
	частицы в пространстве. Эта гипотеза была предложена Дж.Уленбеком и
	С.Гаудсмитом в 1925 г. для объяснения ряда особенностей спектров излу-
	чения атомов, о которых будет сказано в следующих главах. Такой момент
	называется собственным моментом импульса, или спином							Ls (от англий-
	ского слова "spin" – кружение, верчение). Величина спина Ls							строго фикси-
	рована для каждойчастицы ине может меняться.
			С классической точки зрения момент импульса, не связан-
			ный с движением в пространстве, можно связать только с вра-
			щением частицы вокруг собственной оси (рис.6.10). Тогда мож-
			но проквантовать собственный момент импульса аналогично
			моменту L = [r ,		p]	и получить формулы для разрешенных зна-
Рис.6.10			чений величины		Ls	и его проекции на выделенную ось Ls z ,
			аналогичные формулам (6.16) и (6.20):
		Ls	= s (s +1);	Ls z =		σ, где σ = ..., ±(s −1), ± s	.	(6.25)
	Величины спина Ls			и его проекции Ls z определяются двумя кванто-
выми числами s и σ . Число s						называют спиновым квантовым числом (а

часто – просто спином).

Замечание: величина спина электрона, следующая из эксперимента, Ls = 9,14 10−35 кг м2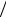с. Если считать электрон шариком радиуса r с мо-

ментом инерции I = 2me r2 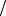5 , вращающимся вокруг своей оси с угловой скоростью ω = Ls 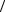I , то скорость движения точки на поверхности шарика

v = ω r = 5Ls 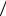(2 me r) . До сих пор размер электрона не измерен, по край-

ней мере, он много меньше размера атомного ядра (r 10−15 м). Чтобы

при вращении частицы с таким радиусом возник момент импульса Ls с приведенной выше величиной, должно нарушаться основное требование теории относительности v = ωr < c = 3 108 мс , что невозможно.

Вывод: спин микрочастиц не связан с действительным вращением в пространстве. Это – квантовое свойство. Даже если размер частицы равен

нулю, она ведет себя так, как если бы вращалась с моментом импульса Ls .

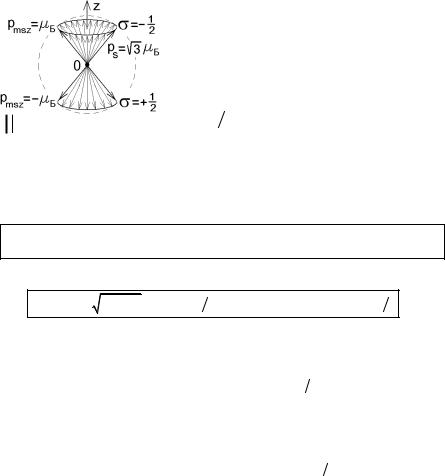
5. Спин

97

Сотсутствием реального вращения связаны две особенности спина.

1)В отличие от целых квантовых чисел l и m , спиновое число s может быть как целым, так и полуцелым. Для фотона s = 1; для электрона,

протона, нейтрона s =12 .

2) С собственным моментом импульса связан собственный магнитный момент pm s . Но гиромагнитное отношение для него аномально,

оно в два раза больше отношения (6.22). Для электрона
pm s = −(e me )Ls .	(6.26)

Формула (6.26) была проверена экспериментально в опытах Эйнштей- на-де Хааза (рис.6.7) в случае ферромагнитного цилиндра. Величина pm

определялась по создаваемому намагниченным цилиндром магнитному

полю, а величина L – по углу закручивания нити подвеса. Их отношение оказалось равным e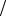me , т.е.

ферромагнетизм обусловлен собственными магнитными моментами электронов, а не токами намагничивания.

С учетом (6.25) и (6.23) формулы квантования собственного магнитного момента электрона имеют вид:

pm s = 2µБ s (s +1), где s =1 2; pm s z = −2µБ σ, где σ = ±1 2 .(6.27)

	И спин	Ls , и собственный магнитный
	момент электрона		pm s	могут иметь только
	две проекции на любую выделенную				ось
	(рис.6.11):	L s z = ±	2;	pm s z = ±µБ .	Это
	объясняет результат опыта Штерна-Герлаха
	(рис.6.9): расщепление на два пучка про-
	изошло из-за того, что магнитное поле дей-
Рис.6.11	ствовало на собственный магнитный момент
	электрона:	Fz = pm s z ∂B ∂z .

98

Глава 7

Квантовая теория одноэлектронного атома

1. Одноэлектронный атом в нерелятивистском приближении

Определим свойства квантовой системы, образованной электроном, движущимся в поле массивного неподвижного ядра с зарядом +Ze. Полуклассическаямодельтакоговодородоподобногоатомаужебыларассмотренав§2 гл.3.

Электрон с массой me находится в бесконечно глубокой кулоновской

потенциальной яме (рис.7.1), и его волновая функция будет решением стационарного уравнения Шредингера (4.34):

	2m	e			k Ze	2
∆ψ(r,θ,ϕ)+			E	+			ψ(r,θ,ϕ)= 0,	E < 0 .	(7.1)
	2				r
				Определим такую волновую функцию ψ ,
			которая одновременно являлась бы собствен-
			ной функцией оператора полной энергии (ре-
			шением уравнения (7.1)), а также операторов
			квадратов момента импульса и магнитного мо-
			мента и их проекций на ось z. Все эти операто-
			ры коммутируют друг с другом и, следователь-
			но, для электрона в атоме одновременно мож-
			но найти разрешенные значения всех величин
Рис.7.1			E, L, pm ,				Lz и pm z .

Учтем, что оператор ˆ2 (6.18) пропорционален угловой части оператора Лап-

L

ласа, записанного в сферических координатах:

1

∂

2

∂

1

∂

2

∂

1

∂

2

1

∂

2

∂

ˆ2

L

∆ =

r

+

+ ctgθ

+

=

r

−

(7.2)

2

2

2

2

2

2

2

2

r

∂r

∂r

r

∂θ

∂θ

sin

θ ∂ϕ

r

∂r

∂r

r

Это позволяет разделить переменные

ψ(r,θ,ϕ)= f (r )Y m

(θ,ϕ),

(7.3)

l

где Ylm – сферические функции. Подставляя (7.2) и (7.3) в (7.1) и, учитывая фор-

мулу (6.19), приходим к уравнению для определения радиальной части волновой функции:

1

∂

∂ f

æ2

2Z

l (l +1)

r2

−

−

+

f = 0 ,

(7.4)

r2

r1 r

r2 ∂r

∂r

r2

1

где введены положительные константы

1. Одноэлектронный атом в нерелятивистском приближении

99

2
r1 = k me e2	и

Как видно из формулы (3.21), r1

æ2 = −	2 2E	= −	2me	E	r2	. (7.5)
	k2 m e4
			2	1
	e

– это радиус первой боровской орбиты. Приведем

уравнение (7.4) к более удобному для решения виду, совершая замену функции

f (r) = R(r) r ,

(7.6)

а затем вводя новую безразмерную переменную ξ = r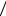r1 . В результате преобра-

зований получим					l (l +1)
	d 2 R	+	2Z	R −		R −æ2R = 0 .
	dξ2		ξ		ξ2
После подстановки		R(ξ) = e−æξ ξl+1 g(ξ)					(7.7)

и после вычисления всех производных это уравнение приводится к дифференциальному уравнению для определения неизвестной функции g(ξ) :

ξ	d 2 g	+(2l + 2 −2æξ)	dg	+(2Z −2æ (l +1))g = 0 ,	(7.8)
	dξ2		dξ

которое носит название уравнения Куммера или вырожденного гипергеометрического уравнения. Его решением будет специальная вырожденная гипергеометрическая функция

	Z
	g (ξ)= F		−l −1; 2l + 2; 2æξ .	(7.9)
		æ

Вывод: как видим, волновые функции всех реальных физических систем записываются с помощью довольно сложных специальных функций. Квантовые объекты требуют особого математического языка. Природу нельзя описать, а тем более нельзя понять, используя только правила арифметики и элементарные математические функции.

∞

Запишем решение (7.9) в виде ряда (5.36): g (ξ)= ∑ Ak ξk . После подста-

k =0

новки в (7.8) получим

∑ Ak k (k −1)ξk −1 +(2l + 2)∑ Ak k ξk −1 −

k =2 k =1

−2æ ∑ A k k ξk +(2Z −2æ (l +1))∑ Ak ξk = 0 .

k =1 k =0

В первых двух суммах последнего соотношения сделаем сдвиг индекса суммирования k → k +1 , что позволяет привести его к виду

∞

k∑=0 Ak+1 (k +1)k +(2l + 2)Ak+1 (k +1)−2æ A k k +(2Z −2æ(l +1))Ak ξk = 0.

100	Глава 7. Квантовая теория одноэлектронного атома

Все сомножители при линейно независимых функциях ξk , выделенные квадратными скобками, должны обращаться в нуль, что дает рекуррентное соотношение для определения коэффициентов Ak :

	2æ (k +l +1)−2Z
Ak +1 =	(k +1)(k + 2l + 2) Ak .	(7.10)

При k → ∞ формула (7.10) примет вид Ak +1 ≈ 2æ Ak 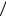k . Но это коэффициенты

∞	(2æξ)k k !. Эта функция, а вместе с
разложения в ряд функции g(ξ) = e2æξ = ∑
k =0

ней и функции (7.7), (7.6) и волновая функция ψ будет бесконечно возрастать при

ξ → ∞ и r → ∞ . Это физически бессмысленно,						так как плотность вероятности
| ψ|2 не может быть бесконечной.
Поэтому	ряд	должен быть конечным – при некотором целом						значении
k = n r = 0, 1, 2,... , которое называют радиальным квантовым числом,								числитель
выражения (7.10) обязан стать равным нулю:
			æ(n r +l +1)	− Z = 0, или æ n = Z ,			(7.11)
где целое число		n = n r +l +1 =1, 2, 3,...			называется главным квантовым числом.
Так как l = n −n		r −1 и l .0 , то величина орбитального квантового числа в од-
ноэлектронном		атоме ограничена		значением		главного	квантового числа:
l = 0, 1, 2, ..., n −1			. Из соотношений (7.5) и (7.11) следует:
			(k2 mee4 ), что позволяет вычислить энергию Е.
æ = Z n =	−2 2E

Разрешенные значения энергии электрона в одноэлектронном атоме, являющиеся одновременно разрешенной энергией самого атома,

		k2Z 2 m e4
	En = −		e	,	n =1, 2, 3,...	(7.12)
		2	2n2

совпадают со значениями, полученными в боровской модели.

Волновые функции всех состояний одноэлектронного атома с разрешенными значениями энергии En выражаются через сферические и вы-

рожденные гипергеометрические функции (их можно найти в математиче-

ских справочниках) по формулам (7.3), (7.6), (7.7), (7.9) и (7.11):

				r	l			2Z r
	ψ	nl m	(r,θ,ϕ) = A			e−Z r n r1 F	−n +l +1; 2l + 2;		Y m (θ,ϕ)		, (7.13)
								n r
			r							l
				1				1