Колмаков Ю.Н. Лекции по физике ТулГУ. Механика / mech-zad-TulGU

Переход в неинерциальную систему отсчета.	21
ряда от вертикали на запад при подъеме и на восток при падении.
Поэтому в проекциях на координатные оси x ' и y ' получим:
a 'x = 2ωv 'y ,	(1.22)
a 'y = −g −2ωv 'x +ω2 R .	(1.23)

Запишем уравнение (1.22) в виде ddtv 'x = 2ωdydt' и, после вычисления инте-

грала ∫dv 'x = 2ω∫dy ' , находим зависимость горизонтальной проекции скорости от высоты подъема:

v 'x = 2ωy ' .

(1.24)

Максимальная высота подъема снаряда h почти не отличается от высоты подъема h0 = v02 2g в покоящейся системе. Действительно, последнее слагаемое в правой части (1.23) пренебрежимо мало по сравнению с ускорением свободного падения: ω2 Rg ≈ 3,5 10−3 (на экваторе Земли). Вертикаль-

ная составляющая кориолисова ускорения направлена вниз и может только уменьшить высоту подъема. С учетом этого замечания, и используя форму-

лу (1.24), находим 2ωv 'x g = 4ω2 y ' g ≤ 4ω2h g ≤ 2ω2v02 g ≈1,1 10−4 .

Вертикальной проекцией кориолисова ускорения в формуле (1.23) можно пренебречь и считать, что a 'y = −g , т.е. движение по вертикальной оси y '

– свободное падение. Поэтому

v '	y	= v − gt	и y ' = v t − gt2	2 .
		0	0

Интегрируя уравнение (1.24) по времени, получаем искомое отклонение снаряда от точки выстрела:

t	v t		2		gt3
x' = ∫v 'x dt = 2ω∫y 'dt = 2ω		0		−		.
		2			6
0

Так как время полета tп = 2v0 g , то окончательно имеем:

	l = x'(tп)=	4ωv3	≈103 м .
		o
		3g2

Итак, снаряд, выпущенный вертикально вверх, упадет на расстоянии 1 км к западу от точки выстрела. Такое большое отклонение показывает, что в задачах баллистики (артиллерия, бомбометание и т.п.) очень важно учитывать вращение Земли.

Глава 2

Динамика.

Динамика поступательного движения

Задача 2.1

На рис.2.1,а две тележки соединены натянутым ремнем, перекинутым через блоки с закрепленными осями вращения. Ремень и блоки невесомы. Массы тележки и стоящего на ней

рис. 2.1 человека m1 =100 кг и m3 =50 кг. Масса второй тележки m2 =150 кг. Как переместится центр масс

системы, если человек пройдет по первой тележке вправо путь l ' =1,8 м в случае а) и в случае б), когда тележки находятся по одну сторону от блоков (рис 2.1,б).

Решение

а) Покоившийся вначале человекGдвижется по тележке с некоторым ускорением aч под действием силы F , с которой на него действует тележ-

ка. Эта сила противоположна силе FG' = −FG , с которой человек толкает тележку. Обе тележки начнут двигаться с одинаковым по величине ускорением a , равным ускорению ремня. Если обозначить силы натяжения рем-

ня вблизи левого и правого блоков как T1 и T2 (рис.2.1,а), то уравнения

движения тележек и человека в инерциальной системе отсчета:

m2a =T2 −T1, m1a = T1 + F −T2 , m3aч = F . (2.1)

Исключая из системы уравнений (2.1) величины сил, находим: aч = (m1 +m2 )am3 = 5a .

Это – ускорение в неподвижной системе отсчета, а относительно тележки человек движется с ускорением

a ' = aч + a = 6a.

(2.2)

Заметим, что последнее уравнение системы (2.1) сразу можно записать в

неинерциальной системе, связанной с первой тележкой, добавляя силу
инерции FGин = −m3aG :	m3a ' = F + m3a.

В этом случае система (2.1) сразу приводит к соотношению (2.2).

рис. 2.2

Динамика поступательного движения

23

Проинтегрировав обе части уравнения (2.2) дважды по времени, находим связь перемещения тележки (или ремня) l и перемещения человека относительно тележки l ' : l ' = 6l .

Относительно неподвижных блоков обе тележки и человек сдвинутся вдоль оси x на отрезки ∆x1 = −l , ∆x2 = +l , ∆x3 = l '−l = 5l . Поэтому, по определению, сдвиг x −координаты центра масс на рис.2.1,а будет:

∆x	=	∑mi∆xi =	m1∆x1 + m2∆x2 + m3∆x3	= l	m2 −m1 +5m3	= l =	l '	= 0,3 м
			m1 + m2 +m3		m1 +m2 +m3
C		∑mi				6

(центр масс переместится вправо, так как результирующая внешних сил 2TG2 +2TG1 , действующая на систему тележки–человек, направлена вправо).

б) В этом случае тележки движутся как одно целое, а величина силы натяжения ремня T слева и справа от них одинакова (при невесомых блоках!, рис.2.1,б). Результирующая внешних сил равна нулю, и центр масс системы смещаться не должен: ∆xC = 0 !

Действительно, система уравнений движения (2.1) примет вид:

(m1 +m2 )a = F +T −T = F, m3aч = F,

откуда по-прежнему следует a ' = 6a и l ' = 6l . Но теперь ∆x1 = ∆x2 = −l ,

∆x3	= l '−l = 5l и		−(m1	+ m2 )l +5m3l
	∆x	=			= 0.
	C		m1	+m2 + m3

Задача 2.2

На плоскость, образующую с горизонтом угол α , положили тяжелую шайбу и толкнули

ее вдоль плоскости с начальной скоростью v0 под углом ϕ0 к ребру наклонной плоскости

(рис.2.2). Найти установившуюся скорость шайбы, если известно, что ее коэффициент трения о наклонную плоскость µ = tgα.

Решение

Уравнение движения шайбы имеет вид: maG = mgG − FGтр . (2.3)

В плоскости движения шайбы на нее действует сила трения, направленная по касательной к траектории, и проекция силы тяжести mg sin α , на-

правленная против оси y (рис.2.2). Проецируя уравнение (2.3) на ось y и на касательную к траектории, находим (рис.2.3):

24					Глава 2. Динамика.
may = −mg sin α− Fтр sin ϕ,					(2.4)
ma	= m	dv	= −F	−mg sin αsin ϕ .	(2.5)
τ		dt	тр

Так как Fтр = µmg cos α = mgtgαcos α = mg sin α , то из уравнений (2.4) и

(2.5) следует, что	may = m dv dt или dvy dt = dv dt , откуда вытекает,
что	vy = v +const .
	Из начальных условий ( vy = v0 sin ϕ0	и v = v0 при
	t = 0 ) находим постоянную интегрирования const=
	= −v0 (1−sin ϕ0 ), поэтому
	vy = v −v0 (1−sin ϕ0 ).	(2.6)
	Проекция скорости на ось x постепенно уменьшает-
рис. 2.3	ся до нуля, так как mdvx dt = −Fтр cos ϕ < 0 . В ре-

зультате при установившемся движении шайба будет скользить с постоянной

скоростью v = vуст	вниз по наклонной плоскости (рис.2.3),			т.е. vy = −vуст .
Следовательно, изуравнения(2.6) получим		vуст =	v0	(1−sin ϕ0 ).
	Задача 2.3	2
	Через закрепленный неподвижный блок с горизон-
	тальной осью перекинута невесомая нить, к концам
	которой прикреплены грузы с массами m1 и m2 .
	Между блоком и нитью имеется трение. Оно таково,
	что нить начинает скользить по блоку, когда отно-
	шение масс грузов m2	m1 = 2 . Найти: а) коэффици-
	ент трения µ, б) ускорение грузов при m2 m1 = 3 .
рис. 2.4		Решение
	При наличии трения между нитью и блоком натя-

жение нити будет различным с разных сторон блока, как показано на рис.2.4. Заметим, что T1 ' = T1 и T2 ' = T2 .

Выделим бесконечно малый участок нити длины dl , прилегащий к блоку (рис.2.5). Он не будет смещаться в радиальном направлении. Поэтому про-

екции на это направление сил натяжения TG и TG+ dTG , растягивающих участок с разных сторон, уравновешены нормальной силой реакции:

dN =T sin (dα2)+(T + dT )sin (dα2)= 2T dα2 (с точностью до малых

	Динамика поступательного движения								25
		первого порядка).
		Сила трения, действующая на выбранный
		участок,		dFтр = µdN = µTdα					направлена по
		касательной к блоку. Так как массой нити
		можно пренебречь, то сумма проекций сил на
		касательное направление также равна нулю. С
		точностью до малых первого порядка получа-
	рис. 2.5	ем изменение силы натяжения нити на эле-
		менте длины dl :
	dF	= (T +dT −T )cos			dα	= dT = µTdα .			(2.7)
	тр			2
					T2		dT	π
	Интегрируя это уравнение по углу α , ∫							= µ∫dα , находим, что при
							T
					T			0
				1
	любом отношении масс грузов					T2 =T1 exp (µπ).			(2.8)
	С другой стороны, из уравнений движения грузов
	m2a = m2 g −T2		и		m1a =T1 −m1g				(2.9)

вытекает, что скольжение начинается при T2 = m2 g и T1 = m1g , т.е. при T2 = 2T1 (так как m2 = 2m1 ). Тогда из уравнения (2.8) получаем:

µ = ln 2π = 0, 2206 .

Итак, каким бы в данной задаче ни было отношение масс грузов,

T2 = T1 exp (πµ)= T1 exp (ln 2)= 2T1 .

С учетом этого, из уравнений (2.9) находим, что всегда

(m	+ 2m )a = (m		−2m )g	или a = g	m2	−2m1	.
2	1	2	1		m2	+ 2m1

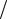В случае m2 m1 = 3 это дает a = g5 .

Замечание. Если нить или канат перекинуть через блок n раз, то на нем можно удержать груз очень боль-

шой массы M , прилагая совсем небольшую силу F

рис. 2.6 (рис.2.6). Например, при F =T1 =1 H , n =10 и µ = 0, 2 ,

µ = 0, 2 , интегрируя уравнение (2.7) по α в пределах от 0 до 2πn −π , получим Mg =T2 = F exp (19πµ)= 15,6 тонн веса

Задача 2.4

Парашютист совершает затяжной прыжок. До раскрытия парашюта он летит со скоростью v1 = 60 м/с , а после раскрытия – приземляется со ско-

26	Глава 2. Динамика.

ростью v2 = 6 м/с. а) Каким было бы максимальное натяжение строп па-

рашюта, если бы он раскрывался мгновенно? б) Каково реальное натяжение строп, если время раскрытия парашюта τ =1 c , и в течение этого вре-

мени натяжение постоянно? Масса парашютиста m = 80 кг, массы строп и

парашюта пренебрежимо малы, а сила сопротивления воздуха прямо пропорциональна квадрату скорости падения.

			Решение
		а) Пусть парашют раскрывается мгновенно в момент
		времени t = 0 при скорости падения v1 = 60 м/с . Немед-
		ленно "включается" сила сопротивления, равная по модулю
		F	= ηv2 , которая затем убывает до величины		F	= ηv2
		1	1		2	2
		(здесь η – коэффициент сопротивления при падении чело-
		века с раскрытым парашютом). Из закона движения сис-
		темы "человек – парашют" (рис.2.7)
	рис. 2.7			m dv dt = mg −ηv2
		следует, что установившаяся скорость падения (то же, что
	и скорость приземления), равная			v2 , определяется условием	dv dt = 0
	или mg = ηv22 , откуда находим:			η = mg v22		(2.10)

Вначальный момент сила сопротивления F максимальна иравна по модулю

Fmax = ηv12 = mg (v1 v2 )2 .

Для парашюта натяжение строп T = F , так как его массой можно пренебречь согласно условию задачи. Поэтому

Tmax = mg (v1 v2 )2 =100mg .

Такой нагрузки в момент мгновенного раскрытия парашюта человек выдержать не может.

б) При постепенном раскрытии парашюта площадь его купола и, одновременно, коэффициент сопротивления η будут расти, а скорость падения

v – уменьшаться. Это позволяет использовать сделанное в условии задачи предположение о том, что произведение ηv2 = F =T ≈ const во время

раскрытия парашюта.

Закон движения человека в интервале времени 0 ≤ t ≤ τ имеет вид:

		dv	v3	τ
	m		= mg −T = const . Интегрируя это уравнение, m ∫	dv = (mg −T )∫dt ,
		dt
			v1	0

рис. 2.8

Динамика поступательного движения						27
находим силу натяжения строп	T = mg +	m	(v	−v	),	(2.11)
		τ 1		3

где v3 – скорость в момент t = τ . В этот момент парашют раскроется полностью, коэффициент η станет равным выражению (2.10) и дальше меняться не будет, а сила натяжения строп, равная силе сопротивления F , начнет уменьшаться со скоростью по закону T = ηv2 . В момент t = τ она

имеет вид

T = ηv

2

= mg (v

v

2

)2 .

(2.12)

3

3

Подставляя формулу (2.11)

в (2.12), получим

v

2

v

v

v

2

v

2

v

v

g

3

= g +

1

−

3

или

3

+

3

− 1

+

1

= 0.

τ

τ

v2

v2

gτ v2

gτ

Решая это квадратное уравнение, находим, что v3 v2 = 2,38 и, оконча-

тельно, T = mg (v3 v2 )2 = 5,66 mg . Такое максимальное натяжение строп в

течение одной секунды парашютист выдерживает.

Задача 2.5

Жидкость в стакане радиуса R вращается с угловой скоростью ω, и на ее поверхности образуется воронка (рис.2.8). Пренебрегая вязким трением в жидкости, определить глубину воронки H .

Решение

Чтобы применить законы динамики к жидкости или газообразной среде, части которой смещаются друг относительно друга, в среде выделяют элемент бесконечно малого объема. Такой элемент на рис.2.8 имеет толщину dx , поперечное сечение ∆S , находится на расстоянии x от оси вращения и может рассматриваться как материальная точка, движущаяся с нор-

мальным ускорением an = ω2 x .

Единственными горизонтально направленными силами, способными создать это ускорение будут силы гидростатического давления: с увеличением расстояния от оси на dx высота столба жидкости над элементом увеличивается на dy, а гидростатическое давление возрастает на dp = ρgdy , где ρ – плотность жидкости. Тогда уравне-

ние движения элемента	dm ω2 x = ∆S (p +dp)−∆S p .
Подставляя массу элемента	dm = ρ∆Sdx , приходим к уравнению

28			Глава 2. Динамика.
ω2 xdx = gdy , которое, после интегрирования			обеих частей, дает
y =	ω2 x2	+const – воронка имеет вид параболы. Ее глубина H = ω2 R2 .
	2g		2g

Приращение импульса

Задача 2.6

Цепочка массы m висит неподвижно, касаясь нижним концом поверхности стола (рис.2.9). Цепочку отпускают. Найти среднюю величину силы давления цепочки на стол за время падения.

Решение

Цепочка падает свободно с ускорением g . Спустя время t на

столе будет лежать участок цепочки длиной h = gt2 2 . Если длина всей цепочки равна l , то вес этого участка P = g hml =

= mg2t2 2l . Оставшаяся часть цепочки будет лететь со скорорис. 2.9 стью v = gt . За последующий бесконечно малый промежуток времени dt на стол упадет элемент цепочки длиной dh = vdt с массой dm = m dh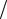l и потеряет скорость. Следовательно, из-за взаимодействием со столом цепоч-

ка за время dt

теряет импульс

dp = v dm , и на стол действует дополни-

тельная сила

F ' =

dp

=

mv2

=

mg2

t2.

dt

l

l

Суммарная

сила,

действующая

со

стороны

цепочки на стол

F = P + F ' = 3mg2t2

(2l ), а ее среднее значение за все время падения

τ = 2l g имеет величину

F

=

1

τ

Fdt =

mg2

τ2

τ−

0

∫

2l

= mg .

0

Неинерциальные системы отсчета и силы инерции

Задача 2.7

На клин с углом α , стоявший на горизонтальной плоскости, был положен брусок (рис.2.10). Трение отсутствует. Оказалось, что оба тела начали двигаться с одинаковыми по величине ускорениями. Найти ускорение клина.

рис. 2.10

Неинерциальные системы отсчета и силы инерции

29

Решение

Пусть массы клина и бруска равны m1 и m2 соответственно, а клин смещается с ускорением aG1 . На рис.2.10 обозначены все силы, действующие на оба тела (брусок действует на клин с такой же по величине силой реакции, с какой клин действует на брусок, NG2' = −NG2 ). Уравнение движения бруска запишем в неинерциальной системе, связанной с клином, добавляя силу инерции FGин = −m2aG1 . В проекции на оси x ' и y ' получим:

m a '		= m g sin α+ m a		1	cos α ,	(	2.13	)
	2 2	2	2
	= N2	+ m2a1 sin α−m2 g cos α .				(	2.14)
0

Уравнение движения клина в инерциальной системе в проекции на ось

x имеет вид:		m1a1 = N2 sin α.							(2.15)
Исключая из уравнений (2.14) и (2.15) силу реакции N2 , находим:
a	1		=	m2 g cos αsin α			.		(2.16)
				m		+ m sin2 α
			1			2
Подставляя соотношение (2.16) в уравнение (2.13), получим:
a '		2	=		(m1 + m2 )g sin α			.	(2.17)
					m1 + m2 sin α

В инерциальной системе, связанной с неподвижным наблюдателем (рис.2.10), горизонтальной и вертикальной проекциями ускорения бруска

будут

a

= a

1

−a' cosα

и a

2 y

= a'

2

sin α , а его величина

a

2

=

a2

+ a2

= a

1

2 x

2

2 x

2 y

по условию. Возводя в квадрат обе части последнего уравнения, приходим к связи a '2 = 2a1 cos α , откуда, с учетом формул (2.16) и (2.17), находим со-

отношение между массами тел:	m1 = m2 (cos2 α−sin2 α). Подставляя это
соотношение в (2.16), определяем:	a1 = gtgα.

Задача 2.8

Небольшое тело поместили на вершину гладкого шара радиуса R. Затем шару сообщили Gв горизонтальном направлении постоянное ускорение a0 , и тело начало

скользить вниз. Найти угол θ0 между вертикалью и ра-

	рис. 2.11	диус-вектором точки отрыва тела от поверхности шара
		(рис.2.11). Вычислить	θ0	при a0 = g .

30	Глава 2. Динамика.

Решение

Уравнение движения тела в неинерциальной системе отсчета, связанной

с шаром, имеет вид:

G

G

G

G

(2.18)

ma = mg

+ N + Fин ,

где NG

–

сила

нормальной

реакции, а

FGин = −maG0

– сила инерции. Проецируя

уравнение (2.18) на направление нормали

nG

к поверхности шара (рис.2.12), получим:

man = mg cos θ− N −ma0 sin θ.

В точке отрыва

NG = 0 , нормальное уско-

рис. 2.12

рение an = v2 R , и поэтому

v

2

= g cos θ

0

−a

sin

θ

0

.

(2.19)

R

0

G

к поверхно-

Проекция же уравнения (2.18) на направление касательной τ

сти (рис.2.12) дает

m

dv

= ma cos θ+mg sin θ.

(2.20)

dt

0

Подставляя длину элемента дуги dl = Rdθ,

проходимой телом за время

dt (рис.2.12), в определение скорости v = dl

dt , находим, что dt = dl v =

= Rdθv . После подстановки этого дифференциала в уравнение (2.20),

приходим к выражению vdv R = dθ(a0 cos θ+ g sin θ)

или

1

d (v2 )= dθ(a0 cos θ+ g sin θ).

(2.21)

2R

(поv ) и от 0 до θ0

Интегрируя уравнение (2.21) в пределах от 0 до v

(по θ ), получаем

v2

= (a

sin θ− g cos θ)

θ0

= a sin

θ

0

− g cos θ

0

+ g .

2R

0

0

0

Подставляя в это выражение значение v2

R в момент отрыва из уравне-

ния (2.19), приходим к равенству 3a0 sin θ0 = 3g cos θ0 −2g .

Возводя его в квадрат, и используя очевидную замену sin2 θ0 =1−cos2 θ0 ,
получаем квадратное уравнение для величины cos2 θ0 :
9(k2 +1)cos2 θ0 −12cos θ0 −9k2 + 4 , где k = a0									g , решение которого име-
		0					(		)
ет вид:	cos θ			2	+5		3 k	2	+1 .
			= 2 ± k 9k