Параллельное программирование

ВВЕДЕНИЕ.

4/09

На пути повышения производительности систем при ускорении элементной базы существуют три ограничения:

• Ограничение снизу – ограничение времени срабатывания элементов.

• Ограниченная скорость распространения электромагнитных сигналов по элементной базе.

• Повышение степени интеграции приводит к необходимости мер по отводу тепла.

Эти факторы естественно ограничивают скорость вычислений. Это приводит к тому, что необходимо использовать параллельные вычисления.

Классификация Флинна.

Флинн предложил классифицировать все существующие ВС следующим образом: соотнести потоки команд и потоки данных в ВС и выделил 4 типа ВС:

SISD

MISD

SIMD

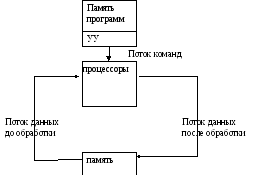
MIMD

Проблемы параллельного программирования:

• Разработка параллельных алгоритмов, которые существенно сложнее обычных последовательных. Как правило, даже разрабатывают сначала последовательный алгоритм, а затем адаптирую к параллельному варианту.

• Оценка эффективности параллельных алгоритмов. Существуют специальные программы, которые на каждом этапе предсказывают возможную эффективность.

• Существуют проблемы синхронизации и проблемы взаимных блокировок.

Параллельные алгоритмы (ПА).

Любая параллельная вычислительная система может быть представлена как совокупность функционально независимых обрабатывающих устройств, осуществляющих обработку информации одновременно. Алгоритм, для реализации на такой вычислительной системе (ВС) должен быть представлен в виде последовательности двух операций, причем все операции одной группы независимы и могут быть выполнены на любом обрабатывающем устройстве системы.

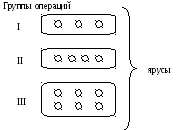
Каждая группа операций (ярус) зависит либо от исходных данных, либо от предыдущих групп. Представленный, в таком виде алгоритм называется параллельным. Он находится в «параллельной форме».

Общее число ярусов называется высотой параллельной формы, а максимальное число операций в ярусе называется шириной параллельной формы.

Теоретически такой алгоритм может быть реализован на параллельной ВС, за время, пропорциональное высоте параллельной формы.

Среди всех возможных параллельных форм одного алгоритма имеется одна или несколько форм минимальной высоты, такие формы называются максимальными и они определяют минимально возможное время выполнения алгоритма на ВС.

Пусть требуется выполнить следующее выражение: (AB+CD)(EF+GH)

Данные: A B C D E F G H

Ярус1: AB CD EF GH 4операции

Ярус2: AB+CD EF+GH 2оп

Ярус3: (AB+CD)(EF+GH) 1оп

Вводится понятие коэффициент ускорения – это общее число операций / на число ярусов. В нашем примере K_y=7/3=2,33.

Для этого же примера можно предложить и другую параллельную форму.

Данные: A B C D E F G H

Ярус1: AB CD 2оп

Ярус2: EF GH 2оп

Ярус3: AB+CD EF+GH 2оп

Ярус4: (AB+CD)(EF+GH) 1оп

Здесь K_у=7/4=1,75

Данные: A B C D E F G H

Ярус1: AB CD 2оп

Ярус2: AB+CD EF 2оп

Ярус3: GH 1оп

Ярус4: EF+GH 1оп

Ярус5: (AB+CD)(EF+GH) 1оп

Здесь K_у=7/5=1,4

ПОСТРОЕНИЕ ПАРАЛЛЕЛЬНОГО АЛГОРИТМА.

11/09

На начальном этапе проектирования параллельного программирования целесообразно использовать так называемую концепцию «неограниченного параллелизма», которая предполагает решение задачи на идеализированной вычислительной системе без учета ограничений реальной вычислительной системы.

Концепция «Неограниченного параллелизма».

Делается предположение, что параллельный алгоритм будет реализован на вычислительной системе, которая не накладывает на него никаких других ограничений кроме числа доступных обрабатывающих устройств. Тогда объектами исследования остаются только высота и ширина параллельной формы.

Идеализированная вычислительная система состоит из необходимого числа обрабатывающих устройств и оперативной памяти произвольного размера, одновременно доступной все обрабатывающим устройствам. Никакие конфликты при обращении к памяти не возникают. Точность выполнения операций так же не учитывается.

Концепция «неограниченного параллелизма» применяется на уровне исследования задачи в целом, позволяет оценить минимально достижимую высоту и загруженность обрабатывающих устройств.

Применение этой концепции включает следующие этапы:

• Расщепление исходной задачи на большие независимые подзадачи.

• Выделение к каждой полученной подзадачи большого потока независимых однотипных подзадач.

• Дальнейшее рекурсивное расщепление подзадач до тех пор, пока не будут получены типовые математические задачи.

• Если типовых задач получается достаточно много и они настолько большие, что можно пренебречь временем обмена данными между ними, то дальнейшее распараллеливание не осуществляется, так как вся задача целиком эффективно решается на системах класса MIMD.

• Если все полученные задачи однотипные, то более выгодной может оказаться решение задачи в целом на системах класса SIMD.

Описанный подход называется крупноблочным распараллеливанием.

Дальнейшее ускорение может быть получено только при распараллеливании типовых математических задач. В настоящее время основное внимание в области параллельных вычислений уделяется созданию методов выявления параллельных структур в традиционных последовательных алгоритмах.

Методы преобразования последовательных алгоритмов в параллельную форму.

Любой последовательный алгоритм включает в себя отдельные участки, относящиеся к одному из следующих типов:

• Линейные участки, которые содержат только последовательно выполняемые операторы, а так же операторы условного и безусловного перехода.

• Выражения

• Рекуррентные соотношения

• Циклические участки (циклы)

Распараллеливание выражений.

Задача: требуется разработать алгоритм, ставящий в соответствие исходному выражению новое выражение, эквивалентное исходному и обладающее минимальным временем реализации.

Все алгоритмы распараллеливания выражений основаны на использовании ассоциативного, коммутативного, дистрибутивного законов. Применение дистрибутивного закона может привести в некоторых случаях к невозможности вычисления нового выражения.

Все алгоритмы распараллеливания выражений делят на две большие группы:

• Методы, основанные на сравнении старшинства операции.

• Методы, использующие обратную польскую запись.

Сравнение старшинства операций.

Входной строкой служит бесскобочная запись исходного выражения. В этой строке выделяются подвыражения, содержащие самые приоритетные операции. Выделенные подвыражения одинаковой глубины склеиваются в более крупные подвыражения, при этом все полученные подвыражения так же имею одинаковую глубину. Весь алгоритм работает за несколько проходов и в результате получается параллельная форма минимальной высоты. Причем, количество проходов определяет высоту полученной параллельной формы.

Параллельная форма для вычисления выражения называется деревом свертки.

Рассмотрим следующий пример.

Пусть требуется вычистить следующее выражение: E = a + b + c * d * l * f + g.

Входная строка	« a+b+c*d*l*f+g »
Результат первого прохода	T1 = (a+b), T2 = (c*d), T3 = (l*f)
Результат второго прохода	« T4+T5 », где T4 = (T2 * T3), T5 = (T1 + g)
Результат третьего прохода	« T6 », где T6 = (T4 + T5)
Выходная строка	(((c*d)*(l*f))+((a+b)+g)))

Результатом работы алгоритма как правило является стек пентад, которые характеризуют ярусы.

Стек пентад.

Уровень	Операция	1операнд	2операнд	Результат
1	+	a	b	T1
1	*	c	D	T2
1	*	l	f	T3
2	*	T2	T3	T4
2	+	T1	g	T5
3	+	T4	T5	T6

Полученный стек пентад может быть эффективно использован в вычислительных системах со стековой организацией.

Метода анализа обратной польской записи.

• Инфиксная запись «a+b»

• Префиксная запись «+ab»

• Постфиксная запись «ab+», она же обратная польская

В этом методе продвигаются по входной строке слева на право до тех пор пока не встречается триада типа: <операнд1><операнд2><операция>. Такая триада имеется хотя бы одна запись. После нахождения такой триады генерируется пентада: «<уровень><операция><операнд1><операнд2><результат>»,

причем уровень равен номеру прохода. Дойдя до конца строки, начинают новый проход, где в качестве операндов используются операнды, незатронутые на предыдущих проходах, а так же промежуточные результаты.

Этот метод не дает в общем случае параллельной формы минимальной высоты.

Входная строка:	«ab+cd*l*f*g++»
Результат первого прохода:	«T1T2l*f*g++», где T1=ab+, T2=cd*
Результат второго прохода:	«T1T3f*g++», где T3=T2l*
Результат третьего прохода:	«T1T4g++», где T4=T3f*
Результат четвертого прохода:	«T1T5+», где T5=T4g+
Результат пятого прохода:	«T6», где T6=T1T5+
Выходная строка:	«(a+b)+((((c*d)*l)*f)+g)»

Данный метод часто используется.

РАСПАРАЛЛЕЛИВАНИЕ РЕКУРСИЙ.

18/09

Рекурсия - это последовательность вычислений, при котором значения очередного вычисляемого терма зависит от одного или нескольких ранее вычисленных термов.

Под термом понимается результаты вычислений на очередном шаге.

Общая линейная рекурсия первого порядка.

X_j = a_jX_j-1+d_j, где j = 1,2,…,n

Частный случай:

X_j = d_k, где j = 1,2,…,n

Рассмотрим традиционную схему вычислений.

Например, n = 8.

0	X1	X2	X3	X4	X5	X6	X7	X8
	d1	d2	d3	d4	d5	d6	d7	d8
	Шаг 1	Шаг 2	Шаг 3	Шаг 4	Шаг 5	Шаг 6	Шаг 7	Шаг 8

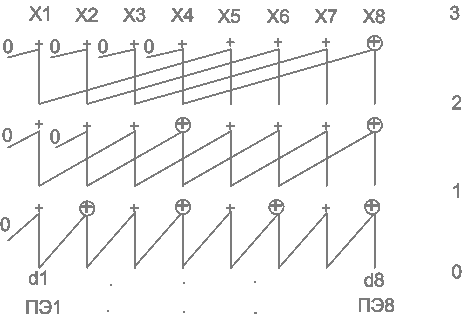
В этом алгоритме:

n-1 операция сложения со степенью параллелизма единица,

n-1 операция сдвига со степенью параллелизма 1.

Шаги:

1. Сначала n аккумуляторов загружаются исходными данными di.

2. Затем на первом уровне производится сдвиг содержимого аккумуляторов на одну позицию вправо и сложение содержимого каждого аккумулятора со сдвинутыми значениями.

3. На втором уровне содержимое аккумуляторов сдвигается на две позиции, на третьем - на четыре и так далее.

В результате на уровне L* = log₂n каждый аккумулятор содержит соответствующую частичную сумму.

В полученном алгоритме log₂n “+” со степенью параллелизма n и n-1 операция сдвига со степенью параллелизма n. Таким образом, общее количество операций сложения выполнены за три шага. Если этот метод применить для получения конечной суммы элементов, не вычисляя всех частных сумм, то общее число сложений получается таким же, как и при последовательном вычислении, а количество шагов равно трем.

Этот алгоритм может быть реализован фрагментом программы на языке Fortran:

X=D

DO 1 L=1, LOG2(N)

X=X+SHIFTR(X, 2**(L-1))

1 CONTINUE

где, X и D – векторы из n элементов,

«+» - параллельное сложение,

SHIFTR – векторная функция, которая помещает копию вектора X со смещением на указное количество позиций (2**(L-1), т.е. 2 в степени (L-1)) вправо, в вектор SHIFTR.

Если вернуться к общей линейной рекурсии первого порядка, то при последовательном вычислении требуется 2n арифметических операций со степенью параллелизма «1» и n сдвигов со степенью параллелизма 1.

Предложенный метод называется методом «каскадных сумм», а соответствующий метод распараллеливания общий рекурсии первого порядка называется «циклической редукцией». На языке Fortran циклическая редукция может быть реализована следующим кодом:

X=D

DO 1 L, LOG 2(N)

X=A*SHIFTR (X, 2**(L-1)) + X

A=A*SHIFTR (A, 2**(L-1))

1

где X, D и A – векторы.

Предложенный метод каскадных сумм может быть использован для вычисления нелинейных рекурсий первого порядка. Например, n!=(n-1)!*n – вот рекурсия первого порядка.

Элементы языка Fortran.

Фортран - язык фиксировано-свободных форматов записи. Любой оператор состоит из 80-ти символов. Состоит из метки (5 символов), далее пробел и до конца - операнды. Если не хватает 80 символов, то можно писать на следующей строке при условии, что шестым символом идет символ, отличный от пробела.

В качестве метки используются только целые положительные числа. Алфавит – только заглавные латинские буквы, знаки арифметических операций.

Если буква С в первой позиции то далее будет комментарий.

Типы данных

INREGER

REAL

LOGICAL (bool)

Все, которые начинаются с I,J,K,L,M,N – по умолчанию целые, а прочие – вещественные.

Явное описание, возможно, любым INTEGER B5.

Неявное описание IMPLICIT REAL J.

Массивы.

Массивы описываются словом DIMENSION A(10,10), в скобках указываются верхние границы индексов, а нижние всегда единица. Максимальное измерение 7. В памяти располагаются по столбцам.

Структура программы.

ОСНОВНАЯ

ПРОГРАММА

ПРОДПРОГРАММА1

ПРОДПРОГРАММА2

…

ПРОДПРОГРАММАn

Каждый раздел заканчивается словом «END». Описание переменных идет сначала раздела.

Подпрограммы начинаются со слов SUBROUTINE или FUNCTION.

Операторы:

1. Оператор присваивания: <переменная> = <выражение>

** - возведение в степень

2. Логические отношения:

.EQ

.NE

.LT

.GT

.GE

.LE

3. Логические операции

.NOT

.AND

.OR

.XOR

4. Логические константы

.TRUE

.FALSE

Переход GOTO <метка>

Логический IF <логическое выражение> <оператор1> <оператор2>

Арифметический IF <арифметическое выражение> (M1, M2, M3)

Если меньше нуля, то переход на M1, равно нулю M2, больше M3.

Цикл

DO <метка> <оператор цикла> = <начальное значение>, <верхняя граница>

<тело цикла>

<метка>

Оператор CONTINUE – аналогия break

Вызов процедуры CALL <имя процедуры> (список операторов)

ЭЛЕМЕНТЫ ЯЗЫКА FORTRAN (продолжение)

25/09

Операторы ввода и вывода

В языке фортран осуществляется форматный ввод и вывод. Это означает что операторы ввода и вывода применяются в паре с форматом, которое может быть помещено в любой части программы.

Обычно номер канала: для ввода 5, для вывода 6.

READ (номер канала, метка формата) список ввода.

WRITE (номер канала) список вывода.

Метка формата это FORMAT (I4, F8.3 …). Каждая спецификация может иметь кратность повторения и заключаться в скобки, например 2(4I4,5F8.3). Работает как цикл. Первый вывод при выводе является управляющим: 1X.

Для размещения введенного формата используются спецификации целых I, (доп. еще E, F), затем идет число позиции, например I4.

Для F – F8.3, затем число позиций после запятой.

Для плавающей запятой E10.5.1 , где второе – для мантиссы, а последнее для изображения чисел после запятой.

Для порядка обозначатся E+01.

Спецификация L – для логических переменных (например, L4), спецификация X – пробег (2X – два пробега)

Для ввода/вывода массива можно использовать неявный цикл

DIMENSION A(5), B(3,3)

…

WRITE (6,1) ((B(I,J), J=1,3), I=1,3)

1FORMAT(1X,3F8.3)

Структура первой лабораторной работы

Описание массивов

<S=10>

Инициализация переменной (присваиваем по одной переменной)

CSBEG

Последовательный участок

CSEND

CPBEG

Параллельный участок

CPEND

Сравнение результатов последовательного и параллельного участка

END

Рекуррентные соотношения

DIMENSION A(10), B(10)

EQUIVALENCE A(1), B(2)

В данном соотношении происходит привязывание переменных A(1) и B(2) к одному и тому же участку памяти.

Распараллеливание линейных участков

Распараллеливание линейных участков применяется главным образом в системах с магистральной обработкой данных, когда одна команда разбивается на ряд последовательных микроопераций, выполняющихся над несколькими аргументами параллельно.

Факторами резко снижающим эффективность таких систем являются:

- команды условных и безусловных переходов,

- информационная зависимость операторов,

- косвенная адресация.

В настоящее время считается, что основной выигрыш при распараллеливании линейных участков получается при выявлении параллелизма на уровне отдельных операторов.

Рассмотрим i-тый участок памяти. Все переменные, которые изменяются на этом учаcтке можно отнести к одной из четырех категорий:

• Только считываемые переменные W_i

• Только записываемые переменные X_i

• Сначала считываемые, а потом записываемые Y_i

• Сначала записываемые, а потом считываемые Z_i

С учетом таких обозначений для любой пары операторов P1 и P2 на этом участке должны выполняться следующие соотношения:

(W1Y1Z1)(X2Y2Z2)=0

(X1Y1Z1)(W2Y2Z2)=0

Если эти условия выполняются, то операторы независимы и могут быть выполнены параллельно.

Алгоритм

Для рассмотрения одного из возможных алгоритмов распараллеливания введем следуюшие обозначения:

I_i – входные данные для i-того оператора, т.е. переменные в правой части оператора присваивания

Oi –выходные данные, т.е. переменные в левой части оператора присваивания.

Для независимости двух операторов i-го и j-го необходимо выполнения следующих соотношений:

Проверка этих условий является основной частью алгоритма автоматического выполнения параллелизма.

Рассмотрим пример:

Пусть исходный линейный участок задан орграфом

Есть матрица смежности для него

C

	1	2	3	4	5	6	7	8
1	0	0	0	0	0	0	0	0
2	1	0	0	0	0	0	0	0
3	0	1	0	0	0	0	0	0
4	0	0	1	0	0	0	0	0
5	0	1	0	0	0	0	0	0
6	0	0	0	0	1	0	0	0
7	0	0	0	1	0	1	0	0
8	0	0	0	0	0	0	1	0

Матрица передачи управления

L

	1	2	3	4	5	6	7	8
1	0	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0	0
3	0	1	0	0	0	0	0	0
4	0	0	0	0	0	0	0	0
5	0	1	0	0	0	0	0	0
6	0	0	0	0	0	0	0	0
7	0	0	0	0	0	0	0	0
8	0	0	0	0	0	0	0	0

Очевидно, что для распараллеливания необходимы еще входные/выходные данные. Они так же представляются булевскими матрицами m на n, где n строк представляют операторы, а m столбцов - идентификаторы переменных. В нашем случае 5 переменных, поэтому матрица 8 строк и 5 столбцов

I

	1	2	3	4	5
1	0	0	0	0	0
2	0	1	0	0	0
3	1	0	0	0	0
4	0	1	0	0	0
5	0	0	0	0	1
6	0	1	0	0	0
7	0	0	1	1	0
8	0	0	0	0	1

O

	1	2	3	4	5
1	0	1	0	0	0
2	0	0	0	0	0
3	0	0	1	0	0
4	0	0	0	1	0
5	0	0	1	0	0
6	0	0	0	1	0
7	0	0	0	0	1
8	0	0	0	0	0

В этих матрицах соответствующий элемент равен единице в том случае если переменная с номером j является входной для оператора I. Для матрицы O, соответственно, та же единица соответствует выходной.

В результате работы предлагаемого алгоритма будет получена матрица C_p и L_p, которые однозначно описывают параллельную форму для исходного алгоритма, и соответствующая граф схема (уже параллельная) будет выглядеть так.

Для построения матрицы C_p сначала строится матрица последовательности выполнения операторов для исходного участка, матрица P.

P

	1	2	3	4	5	6	7	8
1	0	0	0	0	0	0	0	0
2	1	0	0	0	0	0	0	0
0	1	1	0	0	0	0	0	0
4	1	1	1	0	0	0	0	0
5	1	1	0	0	0	0	0	0
6	1	1	0	0	1	0	0	0
7	1	1	1	1	1	1	0	0
8	1	1	1	1	1	1	1	0

В ней отображен порядок следования операторов.

Для построения матрицы C_p необходимо простроить две матрицы P_p (матрица неполного параллелизма) и L_p (матрица параллельной логики).

АЛГОРИТМ ПОСТРОЕНИЯ МАТРИЦЫ C_p

2/10

Алгоритм построения C_p.

1. Стоятся вспомогательные матрицы P_p=P (матрица неполного параллелизма) и L_p=L (матрица параллельной логики)

2. Для всех пар (i, j), для которых элемент матрицы P равен единице («1»), вычисляется функция

IO_i^j = (I_j  O_i) (I_i  O_j) (O_i  O_j)

Если IO_i^j = 0, то операторы i и j – независимы, т.е их можно выполнять параллельно или сохранить последовательность выполнения, для этого случая соответствующий элемент матрицы P устанавливается в нуль (P_Pi^j = 0).

3. Для сохранения логических связей вычисляется элементы

L_Pi = L_i L_j,

где:

Li – i-тая строка матрицы L_p

L_j – j – итая строка матрицы L

В результате логическая связь, ведущая к оператору j будет идти и к оператору i.

4. Строится вспомогательная матрица C_p’= P_P  (), в которой сохраняются только прямые связи длиной 1.

5. Находим искомую матрицу C_p = L_p  C_p’.

Данные матрицы имеют следующий вид:

P_p

	1	2	3	4	5	6	7	8
1	0	0	0	0	0	0	0	0
2	1	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0	0
5	0	0	0	0	0	0	0	0
6	0	0	0	0	0	0	0	0
7	0	0	1	1	1	1	0	0
8	0	0	0	0	0	0	1	0

L_p

	1	2	3	4	5	6	7	8
1	0	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0	0
3	0	1	0	0	0	0	0	0
4	0	1	0	0	0	0	0	0
5	0	1	0	0	0	0	0	0
6	0	1	0	0	0	0	0	0
7	0	0	0	0	0	1	0	0
8	0	0	0	0	0	0	0	0

C_p

	1	2	3	4	5	6	7	8
1	0	0	0	0	0	0	0	0
2	1	0	0	0	0	0	0	0
3	0	1	0	0	0	0	0	0
4	0	1	0	0	0	0	0	0
5	0	1	0	0	0	0	0	0
6	0	1	0	0	0	0	0	0
7	0	0	1	1	1	1	0	0
8	0	0	0	0	0	0	1	0

Недостатки алгоритма.

• Во входных и выходных матрицах массивы рассматриваются как единое целое, анализ элементов не производится

• Если в исходной программе один и тот же идентификатор обозначает разные переменные, то фактически независимые операторы будут считаться информационно-связанными.

Пример.

1 A=B+C

2 D=A+E

3 A=X+Y

4 F=A*Z

На этом линейном участке все операторы должны выполнятся строго последовательно, однако если переписать как указано ниже, то пары операторов 1,2 и 3,4 являются независимы и могут выполнятся параллельно.

1 A1=B+C

2 D=A1+E

3 A=X+Y

4 F=A*Z

Виды зависимостей между переменными:

• информационная

• конкуренционная (1 и 2-го типа)

• транзитивная

РАСПАРАЛЛЕЛИВАНИЕ ЦИКЛОВ

Существует несколько методов:

• Метод гиперплоскостей

• Метод координат

• Метод параллелепипедов

• Метод пирамид

Метод гиперплоскостей.

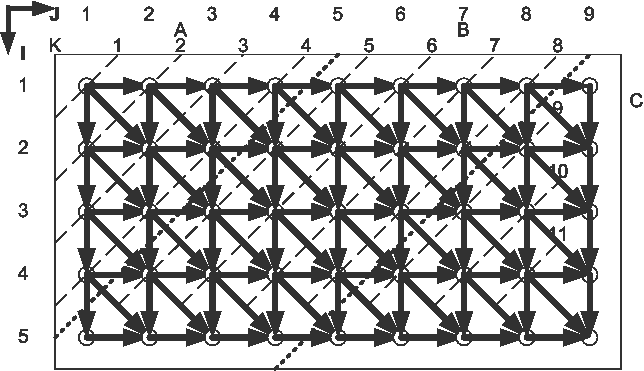
Метод координат.

Метод параллелепипедов.

Метод пирамид.

МЕТОД ГИПЕРПЛОСКОСТЕЙ.

Пусть дан гнездовой циклический алгоритм вида:

DO 99 I=1,L

DO 99 J=2,M

DO 99 K=2,N

V(J,K)=(V(J+1,K)+V(J-1,K)+V(J,K-1)+V(J,K+1))*0,25

99 CONTINUE

Вычисляет среднее арифметическое между четырьмя точками.

Уравнение плоскости: 2*I+J+K = const

Для перехода к параллельному циклу используем переменные:

1 конструкция	2 конструкция	Результирующий (параллельный) цикл
I1, J1, K1: I1=2*I+J+K J1=I K1=K	I, J, K I = J1 J=I1-2*J1-K1 K=K1	DO 99 I=6,2*L+N+M DO 99 CONC FOR ALL (J1, K1)  { ( J1, K1): 1 ≤ J1 ≤ K1, 2 ≤ I1-2*J1-K1 ≤ M, 2 ≤ K1 ≤ N } V ( I1-2*J1-K1, K1 ) = ( V ( I1-2*J1-K1+1,K1 ) + V (I1-2*J1-K1, K1+1 ) + V (I1-2*J1-K1, K1 ) + V (I1-2*J1-K1, K1-1 ) ) *0.25 99 CONTINUE

В 1 конструкции количество повторений равно L*(M-1)*(N-1)

Во 2 новой конструкции 2*L+M+N-5.

Замечание: результирующий цикл записан на параллельном Фортране.

Общая постановка задачи:

Дан

DO A I¹=l¹, U¹

.

.

.

DO A Iⁿ=lⁿ, Uⁿ

<тело цикла>

A CONTINUE

Для использования метода гиперплоскостей необходимо, чтобы тело цикла не содержало:

• операторов ввода–вывода

• передач управления вне цикла

• обращений к процедурам и функциям, которые изменяют переменные в теле цикла.

Индексные выражения в операторах тела цикла должны иметь вид lⁱ+mⁱ, где lⁱ – i-я переменная, mⁱ - i-я константа. Разрешено I+2; запрещено I+J, I*2, I*J.

В результате применения метода гиперплоскостей исходный цикл преобразуется к виду:

DO A J¹=L¹, M¹

.

.

.

DO A J^k=L^k,M^k

DO A CONC FOR ALL (J^k+1, … Jⁿ)  S_Y¹_...Yⁿ

< тело цикла>

A CONTINUE

Происходит свертывание пространственных операций, то есть изменение размерности на N-K

МЕТОД ГИПЕРПЛОСКОСТЕЙ. (продолжение)

9/10

Для нахождения уравнения гиперплоскости строится взаимно-однозначное отображение переменных в теле исходного цикла в новые переменные. Это отображение ищется в виде:

Для нахождения коэффициентов а_jⁿ решается задача линейного целочисленного программирования, в которой формулируется ряд ограничений на коэффициенты а: в исходном и результирующем цикле все использования переменных должны следовать за их генерациями в теле цикла.

a=b.

a – использование, b – генерация.

В лабораторной работе надо будет перейти к двумерным переменным и подобрать коэффициенты:

I₁ = a_{11 *} I + a_{12 *} J

J₂ = a_{21 *} I + a_{22 *} J

[-1 ÷ +1]

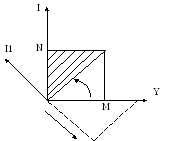
+1 – поворот на 45 градусов против часовой

-1 – по часовой.

Должен получиться один цикл перебора, но с вызовом #CALL () для каждой текущей линии.

Недостатки и достоинства метода.

Достоинством метода гиперплоскостей является то, что он хорошо формализован и, следовательно, он может быть использован в трансляторах с параллельных языков программирования для автоматического распараллеливания циклов.

Недостатком метода является сложность получения алгоритма гиперплоскости а также неприменимость для некоторых видов циклов (в частности для простых циклов).

МЕТОД КООРДИНАТ.

Рассмотрим следующий пример:

Исходный цикл:

DO 24 I=2,M

DO 24 J=1,N

21 A(I,J)=B(I,J)+C(I)

22 C(I)=B(I+1,J)

23 B(I,J)=A(I+1,J)*2

24 CONTINUE

Методом координат этот цикл будет преобразован следующим образом:

DO 24 I=1,N

DO 24 SIM FOR ALL I  {I: 2 ≤ I ≤ M}

21 A(I,J)=B(I,J)+C(I)

23 B(I,J)=TEMP(I)**2

22 C(I)=B(I-1,J)

24 CONTINUE

Здесь, в отличии от метода гиперплоскостей, употребляется конструкция SIM.

SIM конструкция: тело цикла можно выполнять параллельно для нескольких итераций, но необходимо пооператорная синхронизация, т.е. параллельно выполняется первый оператор цикла для всех итераций, и только по окончании выполнения этого оператора во всех итерациях осуществляется переход ко второму оператору и так далее.

Из примера видно, что значения, вычисленные оператором 23 в i-той итерации используется в операторе 22 в i+1-ой итерации, что и мешает их независимой работе.

Из этого примера так же видно, что для эквивалентности исходного и полученного цикла пришлось вводить дополнительную переменную TEMP и менять метами 23 и 22 операторы, то есть осуществлять неформальные преобразования.

Достоинства метода:

1. Если рассмотренный пример решать методом гиперплоскостей, то при переходе к новым переменным

получаем M+N-2 повторений, а для метода координат - N повторений.

2. Метод координат не требует сложных преобразований индексов.

3. Метод применим и для простых циклов. Наиболее целесообразно использовать метод координат при распараллеливании в системах класса SIMD.

Рассмотренный ранее пример для метода гиперплоскостей не может быть решен методом координат. Для каждого вида цикла подходит тот или иной метод.

МЕТОД ПАРАЛЛЕЛЕПИПЕДОВ.

В этом методе подмножества независимо выполняемых операций ищутся в форме прямоугольных параллелепипедов. Данный метод так же применим и для простых циклов.

Рассмотрим следующий пример.

DO 2 I=1,15

X(I)=X(G*I-27)

2 CONTINUE

В этом примере рассматривается одномерный случай пространства итераций, и в результате параллельный счет осуществляется для точек, принадлежащий отрезку прямой длиной = 4.

DO 2 I=1, 4

DO 2 CONC FOR ALL J  { 4*(I-1) ≤ J ≤ MIN {4*I,15} }

X(I)=X(G*I-27)

2 CONTINUE

Общая постановка задачи.

Пусть I={I₁,I₂,…,I_n} – исходное пространство итераций. Требуется найти такие целые числа, P₁,P₂,…,P_n, называемые ребрами параллелепипеда, при которых исходные конструкции вида

DO 1 I₁=1,R₁

DO 1 I₂=1,R₂

……

DO 1 I_n=1,R_n

<ТЕЛО ЦИКЛА>

1 CONTINUE

ставится в соответствие эквивалентная конструкция вида

DO 2 CONC FOR ALL J  {1,N}

DO 2 K_j=1, P_j

DO 2 I₁=K₁, R₁, P₁

DO 2 I₂=K₂, R₂, P₂

……

DO 2 I_n=K_n, R_n, P_n

<ТЕЛО ЦИКЛА>