4.2. Задача производителя и ее свойства

145

В векторных обозначениях,

κrg(y¯) = p,

то есть градиент неявной производственной функции коллинеарен вектору цен.

Если не все цены равны нулю (p 6= 0), то κ > 0. Исключая множитель Лагранжа κ, для любых двух благ k, s K , таких что pk 6= 0, получаем, что

ps = ∂g(y¯)/∂ys . pk ∂g(y¯)/∂yk

Следовательно, решение задачи производителя характеризуется равенством предельной нормы трансформации любых двух благ отношению цен этих благ.

Условия первого порядка задают систему уравнений, любое решение которой по обратной теореме Куна — Таккера является решением задачи производителя, если выполнено дополнительное условие, что функция g(·) вогнута.

4.2.1Задачи

/193. Объясните, почему при не равных нулю ценах решение задачи производителя должно лежать на границе технологического множества.

/194. Докажите, что все точки эффективной границы выпуклого технологического множества являются решением задачи производителя при некоторых неотрицательных, не равных нулю ценах. Приведите пример, показывающий, что в этом утверждении нельзя заменить неотрицательные цены на положительные.

/195. Для случая, когда технологическое множество может быть представлено посредством производственной функции, сформулируйте и докажите лемму Хотеллинга, пользуясь формулой вычисления прибыли и условиями первого порядка для внутреннего решения задачи производителя.

/196. Для случая, когда Y представлено дифференцируемой неявной производственной функцией, можно доказать лемму Хотеллинга используя теорему Куна — Таккера. Проведите это доказательство. (Подсказка: см. первое доказательство леммы Шепарда для теории потребления).

/197. Докажите Теорему 53.

/ 198. Покажите, что если производственная функция f(·) строго вогнута, и, кроме того, f(0) = 0, то прибыль в точке оптимума неотрицательна.

/199. Покажите, что если производственная функция в точке максимума прибыли обладает возрастающей отдачей от масштаба, то прибыль не может быть положительной. На основании этого выведите, что в случае возрастающей отдачи от масштаба задача производителя либо не имеет решения, либо в точке решения прибыль равна нулю.

/200. Пусть r(w, po) — функция спроса на факторы, yo(w, po) = f(r(w, po)) — функция предложения, а H = r2f(r) — матрица вторых производных производственной функции f(r). Выведите следующие соотношения сравнительной статики для задачи производителя:

∂yo

1

rfH−1rf,

∂r

1

H−1rf,

= −

= −

∂po

po

∂po

po

∂yo

1

H−1rf,

∂r

1

H−1.

=

=

∂w

po

∂w

po

На основании этого сделайте заключение о поведении выпуска производителя и его спроса на факторы для вогнутых производственных функций. Проиллюстрируйте эти соотношения для производственной функции типа Кобба — Дугласа.

4.2. Задача производителя и ее свойства

146

/ 201. Пусть множество производственных возможностей фирмы задается условием:

y1 6 ln(1 − y2), где y2 < 1.

Постройте функции спроса (предложения) на y1 , y2 . Постройте функцию прибыли для данной технологии.

/202. Для технологии, описываемой производственной функцией f(r) = rα , вычислите:

-функцию прибыли,

-функцию спроса на производственный фактор,

-функцию предложения,

Покажите, что

-функция прибыли однородна и выпукла (по цене продукции, po , и цене производственного фактора, w),

-функция спроса удовлетворяет закону спроса,

-функция предложения удовлетворяет закону предложения

/203. Найдите функцию прибыли, функцию предложения и функцию спроса на факторы для перечисленных производственных функций:

(а) f(r) = Qi riαi , αi > 0 (функция Кобба — Дугласа),

(б) f(r) = Pi airiρ ,

(в) f(r) = Pn−1 fi(ri) + rn .

i=1

Какими свойствами обладают найденные функции? Покажите, что для данных функций выполнена лемма Хотеллинга.

/204. Докажите, что валовой доход фирмы, не может вырасти, если цены на все факторы производства увеличатся пропорционально.

/205. Покажите, что валовой доход фирмы не может вырасти, если упадет цена по крайней мере одного из выпускаемых ею продуктов.

/206. Покажите, что прибыль фирмы упадет, если вырастет цена по крайней мере на один из используемых ею факторов производства.

/207. Покажите, что прибыль фирмы упадет, если упадет цена по крайней мере на один из выпускаемых ею продуктов.

/208. Предположим, что производственная функция для некоторой технологии вогнута и сепарабельна, причем предельный продукт любого фактора производства как угодно мал при достаточно больших объемах затрат этого фактора производства. Покажите, что

-валовой доход фирмы упадет, если возрастет цена по крайней мере на один из используемых ею факторов производства;

-функция спроса (предложения) данной фирмы удовлетворяет условиям валовой заменимости;

-спрос данной фирмы на любой фактор производства неограниченно возрастает при падении цены этого фактора производства;

-предложение данной фирмы неограниченно возрастает при росте выпускаемой этой фирмой продукции.

/209. Покажите, что в случае однородной производственной функции показатель отдачи от масштаба не зависит от цен факторов.

/210. Покажите, что в случае однородной производственной функции отношение функций спроса на любые два фактора производства не зависит от цены продукции.

/211. Покажите, что функция прибыли сепарабельна тогда и только тогда, когда сепарабельна функция спроса.

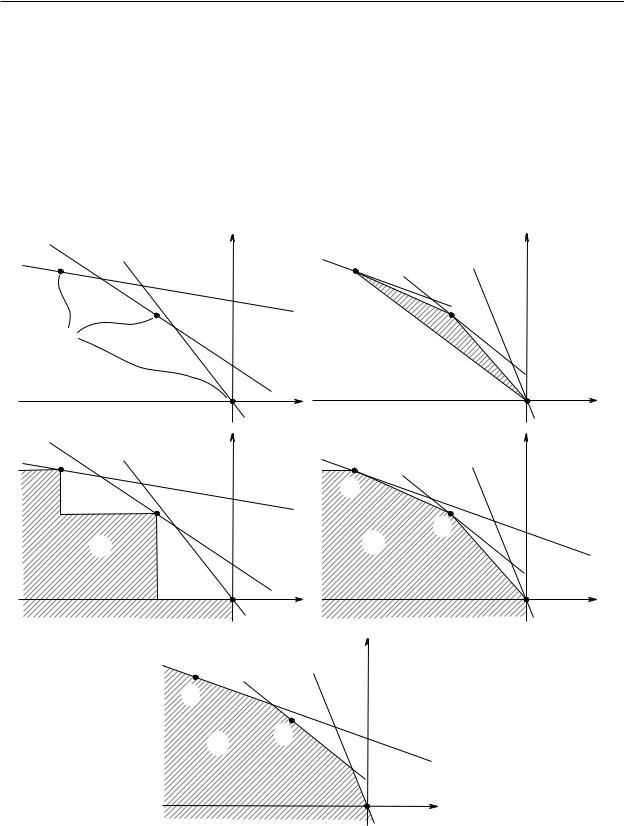
4.3. Восстановление технологического множества	147

4.3Восстановление технологического множества

Аналог концепции выявленных предпочтений для модели производителя имеет довольно простой вид. Пусть (pi, yi), i = 1, . . . , n — последовательность наблюдений: при ценах pi наблюдался вектор чистого выпуска yi . Если при каком-то векторе цен pi выполнено piyj > piyi , то yi не максимизирует прибыль при ценах pi . А это противоречит рациональности производителя.

Если же piyj 6 piyi i, j , то последовательность наблюдений (pi, yi), i = 1, . . . , n не противоречит гипотезе максимизации прибыли. Технологическое множество, которое порождает такие выборы производителя, может быть построено разными способами. Рассмотрим некоторые из них.

	(1)	(2)
y1		y1
		y2
y2
Y1		Y2
	y3	y3
	(3)	(4)
y1		y1
y	2	y2
		Y4
Y3
	y3	y3

y1 (5)

y2

Y5

y3

Рис. 4.8. Возможные способы восстановления множества Y по наблюдаемым точкам

4.3. Восстановление технологического множества

148

Наиболее простым является вариант, когда технологическое множество, которое при максимизации прибыли порождает такие выборы, состоит только из точек yi , т. е.

Y1 = {y1, y2, . . . , yn}.

Также можно в качестве технологического множества Y можно взять выпуклую оболочку Y2 точек y1, y2, . . . , yn (если мы предполагаем, что технологическое множество выпукло). Если мы предполагаем выпуклость и свободу расходования, то в качестве Y можно взять разность

между Y1 и Rl+ :

Y3 = Y1 − Rl+,

и между Y2 и R+ :

Y4 = Y2 − Rl+.

Еще один вариант — пересечение полупространств, отсекаемых соответствующими гиперплос-

костями:

Y5 = { y | piy 6 piyi, i = 1, . . . , n } .

Все эти варианты для случая n = 2 изображены на приведенных выше рисунках. Прямые, нарисованные пунктиром, изображают цены. Отметим, что

Y1 Y2 Y4 Y5

и

Y1 Y3 Y4 Y5.

Таким образом, существует несколько множеств, порождающий указанный спрос, причем Y5 является «максимальным» из этих множеств (т. е. содержит любое другое множество). Покажем, что аналогичная процедура позволяет построить подходящее технологическое множество и в случае, когда количество наблюдений может быть бесконечно.

Предположим, что функция y(p), определенная на множестве цен P , такова, что y(p) является решением задачи максимизации прибыли при ценах p. Требуется на основе y(p) и соответствующей функции прибыли π(p) восстановить соответствующее технологическое множество Y .

Заметим, что существование вектора y Y , такого что py > π(p) при некоторых ценах p, противоречило бы гипотезе максимизации прибыли на Y . Объединим все векторы y не противоречащие этому условию при всех неотрицательных??

\

Yπ = { y | py 6 π(p) } = { y | py 6 π(p) p P } .

p P

Очевидно, что по построению выполнено Y Yπ (т. е. построенное технологическое множество будет в общем случае шире, чем исходное), и y(p) является решением задачи производителя с технологическим множеством Yπ при ценах p P . Как следствие, функция прибыли для технологического множества Yπ определена при всех p P и совпадает с π(p).

Таким образом, мы нашли (максимальное) технологическое множество, которое порождает данные наблюдения.

Уместен вопрос: совпадет ли множество Yπ с технологическим множеством Y , на основе которого оно построено? Положительный ответ на этот вопрос позволил бы нам восстанавливать технологические множества по наблюдаемому поведению.

Ответ на вопрос зависит от свойств технологического множества Y и от множества цен P , при которых наблюдается предложение.

В общем случае Y и Yπ могут не совпадать, поскольку описанный метод построения Yπ порождает выпуклые множества (пересечение полупространств), а технологическое множество

4.3. Восстановление технологического множества		149
Y	может быть невыпуклым (как на Рис. 4.8.1 и 4.8.3). Кроме того, ясно, что множество цен
P	может быть недостаточно «богатым» для того, чтобы технологическое множество было
адекватно представлено наблюдаемыми выборами при этих ценах.

Рассмотрим частный случай, когда P = Rl++ . В этом случае Y и Yπ могут не совпадать, поскольку наш метод построения Yπ порождает множества, удовлетворяющее свойству свободы расходования, а технологическое множество Y может не удовлетворять свойству свободы расходования (как на Рис. 4.8.1 и 4.8.2).

Теорема 54:

Пусть технологическое множество Y непусто, замкнуто, выпукло и удовлетворяет свойству свободы расходования. Тогда при P = Rl++ оно совпадает с порождаемым им множеством Yπ .

Доказательство: Поскольку Y Yπ , то остается показать только, что Yπ Y .

Рассмотрим точку y˜ , не принадлежащую технологическому множеству Y . По теореме отделимости для непустого выпуклого замкнутого множества Y и точки y˜ , не принадлежащей этому множеству, существует вектор коэффициентов p˜ , не равный нулю, и число q, такие что

p˜y˜ > q > py˜ y Y.

Покажем, что p˜ может быть вектором цен. Для этого нужно, чтобы он не имел нулевых или отрицательных компонент.

Предположим, что p˜i < 0. Рассмотрим некоторую точку y0 Y и луч y0 − λei при λ > 0, где ei — орт (i-я компонента равна 1, а остальные — нули). Этот луч целиком лежит во множестве Y , так как Y удовлетворяет свойству свободы расходования. Величина py˜ 0−λp˜i не ограничена сверху. Это противоречит тому, что p˜y˜ > py˜ y Y . Мы пришли к противоречию, поэтому p˜ > 0.

Более того, можно выбрать вектор коэффициентов так, что в нем не будет нулевых компонент. Действительно, рассмотрим вектор p˜ + εp0 , где p0 — произвольный вектор цен из Rl++ . Величины p0y при y Y ограничены сверху значением π(p0), поэтому, если ε достаточно мало, то все еще будут выполняться неравенства

(p˜ + εp0)y˜ > (p˜ + εp0)y y Y.

Следовательно, существует вектор p˜ > 0, такой что p˜y˜ > py˜ y Y . Отсюда следует, что p˜y˜ > π(p˜), и, значит, y / Yπ .

Мы показали, что любая точка, которая не принадлежит Y , не принадлежит и Yπ . А это значит, что Yπ Y .

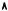y2

y˜

Y

y1

Рис. 4.9. Иллюстрация отделимости

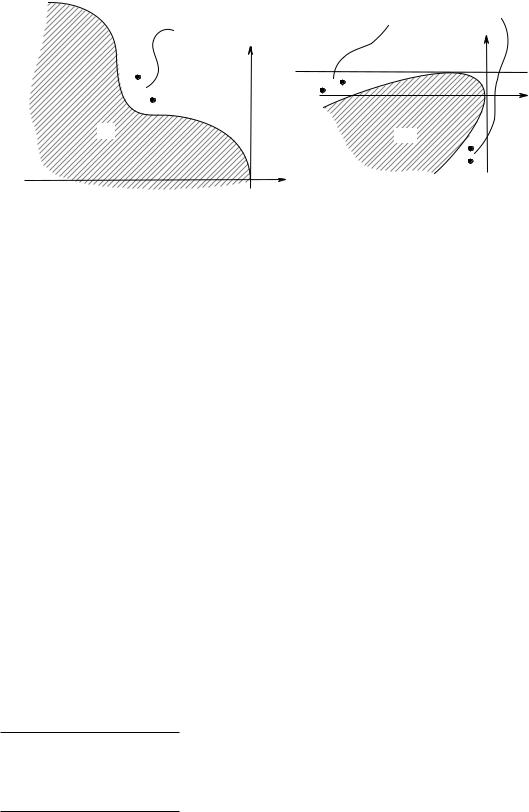
Ниже Рис. 4.10 приведены примеры ситуаций, когда при нарушении предположений теоремы ее утверждение (Yπ Y ) неверно и, тем самым, невозможно восстановить Y на основе функции прибыли.

4.3. Восстановление технологического множества	150
	Эти точки нельзя отделить
Эти точки	гиперплоскостью с
	неотрицательным наклоном
нельзя
отделить	y2
y2
	y1
Y	Y
y1
Не выполнено условие выпуклости	Не выполнено условие свободы
	расходования

Рис. 4.10. Ситуации, когда невозможно восстановить Y .

Обсудим теперь следующую проблему: как для данной функции π(p) и функции y(p), заданных на множестве цен P , определить, могут ли они являться соответственно функцией прибыли и функцией предложения рационального производителя?

Понятно, что необходимыми требованиями к функции прибыли являются ее выпуклость, однородность первой степени и непрерывность. Оказывается, что эти условия являются и достаточными для того, чтобы произвольная функция π(p) была функцией прибыли для некоторого технологического множества. В качестве такого множества можно взять рассмотренное выше множество

Yπ = { y | py 6 π(p) p P } .

Следующий набор утверждений формализует сказанное выше:

(1)Если функция π(p) удовлетворяет набору необходимых условий для функции прибыли, то построенная на ее основе функция y(p) удовлетворяет набору необходимых условий для функции предложения производителя.

(2)Если функция y(p) удовлетворяет набору необходимых условий для функции предложения производителя, то построенная на ее основе функция π(p) удовлетворяет набору необходимых условий для функции прибыли.

(3)Если функция π(p) удовлетворяет набору необходимых условий для функции прибыли, то существует технологическое множество, порождающее π(p) как функцию прибыли.

Перечислим упомянутые необходимые условия. Для удобства доказательства потребуем дополнительно, что π(p) является дважды непрерывно дифференцируемой, а y(p) — непрерывно дифференцируемой.

Условия на функцию π(p):

(A1) положительная однородность первой степени; (A2) выпуклость;

(A3) π(·) дважды непрерывно дифференцируема (более сильное условие, чем требуется).

Условия на функцию y(p):

(B1) положительно однородна нулевой степени,

(B2) матрица производных M = {∂ys/∂pk} существует и непрерывна, положительно полуопределена и симметрична.

Сформулируем приведенный выше набор неформальных утверждений как теорему.

4.3. Восстановление технологического множества			151
Теорема 55:
(1) Пусть	∂π(p)
yk(p) =		,
	∂pk

где функция π(p) удовлетворяет условиям (A1), (A2), (A3).

Тогда y(p) = (y1(p), . . . , yl(p)) удовлетворяет условиям (B1), (B2) налагаемым на функцию спроса-предложения производителя.

(2) Пусть функция y(p) удовлетворяет условиям (B1), (B2).

Тогда функция π(p) = py(p) удовлетворяет условиям (A1), (A2), (A3).

(3) Пусть функция π(p) удовлетворяет условиям (A1), (A2), (A3). Тогда множество Yπ = { y | py 6 π(p) p > 0 } является технологическим множеством порождающим функцию прибыли π(p).

Доказательство: (1) (A1)-(A3) (B1)-(B2).

Поскольку функция π(p) однородна первой степени, то ее производная y(p) однородна нулевой степени.

Непрерывная дифференцируемость y(p) следует из дважды непрерывной дифференцируемости функции π(p).

Матрица вторых производных любой дважды непрерывно дифференцируемой функции симметрична. Применяя это свойство к функции π(p) имеем,

∂2π(p) = ∂2π(p). ∂ps∂pk ∂pk∂ps

Матрица вторых производных функции π(p) есть матрица первых производных функции y(p). Поэтому

∂ys = ∂yk . ∂pk ∂ps

Положительная полуопределенность матрицы вторых производных (то есть rMr > 0 r Rn ) — необходимый (и достаточный) признак выпуклости любой дважды дифференцируемой функции.

(2) (B1)-(B2) (A1)-(A3).

P

Продифференцируем π(p) = py(p) = pkyk(p) по pk :

	∂π(p)		l	∂ys(p)			l	∂yk(p)
		= yk(p) +	ps			= yk(p) +	ps		.
	∂pk		X	∂pk			sX	∂ps
			s=1				=1

Второе равенство — следствие симметричности производных функции y(p). Так как y(p) — положительно однородна нулевой степени, то по закону Эйлера

l

X ps ∂yk(p) = 0.

s=1 ∂ps

Таким образом,

∂π(p)

∂pk

= yk(p).

Далее воспроизводим доказательство пункта (1) в обратном порядке.

(3)

Обозначим

y(p) = rπ(p).