Теория вероятностей. Чудесенко. 25 Вариант

Ч_2_30_25

Двумерная случайная величина ( ξ, η ) имеет равномерное распределение
	1/ S,	.		ru
вероятностей в треугольной области ABC , т.е.	p(x, y) =	если (x, y) Î ABC	,
	0 ,

где

S - площадь

ABC .

Определить

маргинальные плотности распределения pξ (x)

и pη ( y)

случайных величин

ξ и η ,

математические ожидания

Mξ, Mη, дисперсии

Dξ, Dη ,

коэффи-

циент корреляции r .Являются ли случайные величины

ξ и η

независимыми? Указаны декартовы

координаты вершин

ABC :

A(0;−1),

ξ antiGTU∫

B (−1; 0),

C(1;

0) .

Решение.

Сделаем чертеж, и найдем площадь

ABC .

S =

1

× AO × BC =

1

×1× 2 = 1,

1 ,

если (x, y) Î ABC

Очевидно,

что

поэтому

p(x, y) =

если (x, y) Î ABC

2

2

0 ,

Прямая AB имеет уравнение y = −x −1 x = −y −1;

прямая AC имеет уравнение y = x −1 x = y +1 .

Плотность распределения случайной величины

pξ (x)

случайной величины ξ

выражается

формулой p (x) =

+∞

через совместную плотность

p(x, y)

p(x, y)dy . Аналогично для

Скачано

−∞

+∞

η

имеем: pη ( y) = ∫

p(x, y)dx .

плотности

распределения

случайной

величины

называютсяс

−∞

Одномерные плотности

pξ (x) и

pη ( y)

маргинальными.

Т.к. вне

ABC

плотность

p(x, y)

равна

0 ,

то

при

x [−1; 1]

pξ (x) = 0 .

Из чертежа следует,

что

ABC

следует разделить на две части :

+∞

0

0

при

x [−1; 0]

pξ (x) = ∫

p(x, y)dy =

∫ 1× dy = y

−x−1

= 1+ x;

−∞

−x−1

+∞

0

1

при

x [ 0; 1]

pξ (x) = ∫

p(x, y)dy = ∫ 1× dy = y

= 1- x .

−∞

x−1

x−1

1+ x,

x Î[-1; 0]

x Î[

0;1] .

Получаем

pξ (x) = 1- x,

,

x Î[-1;1]

0

+∞

y +1

y +1

при

y [−1; 0]

pη ( y) = ∫

p(x, y)dx =

∫

1× dx = x

− y −1

= 2( y +1);

−∞

− y −1

pη ( y) =

2( y +1),

y Î[ -1; 0]

Получаем:

0

,

.

y Î[ -1; 0]

Две случайные величины ξ и η являются независимыми тогда и только тогда,

когда выпoлняется условие														p(x, y) = pξ (x) × pη ( y) .																							(1).																																	ru
В данном случае равенство (1) не выполняется, значит величины ξ и
																																																					η являются зависимыми
Находим математические ожидания и дисперсии величин ξ и η :
+∞								0						1												x	2		x	3			0					x			2					x		3				1					1					1						1			1
Mξ = ∫ xpξ (x)dx = ∫ x ×(1+ x)dx + ∫ x ×(1- x)dx = (																												+				)		+ (									-							)		= -(								-					) + (				-				) = 0 ;
																								2				3					antiGTU																											3					2						3
−∞								−1						0																			−1																		0
+∞														0					1																	x			3					x			4				0			x		3					x			4	1
Dξ = ∫ x2 pξ (x)dx - (Mξ )2 = ∫ x2 (1+ x)dx + ∫ x2 (1- x)dx - 02 = (																																										+							)				+ (					-							).=
−∞														−1					0																		3					4									−1		3							4					0
= -(-	1	+	1	) + (		1	-		1	) =			1	;
3		4			3			4			6
+∞								0									y	3			y	2		0									1		1											1
Mη = ∫ ypη ( y)dy = ∫ y × 2( y +1)dy =2 ×(																			+				)	-1			= -2(-							+			) = -											;
−∞								−1								3			2														3 2									3
+∞														0										1							y		4		y		3					0							1						1						1					1				1
Dη = ∫ y2 pη ( y)dy - (Mη )2 = ∫ y2 × 2( y +1)dy - (-																									)2 = 2 ×(									+						)		-									= -2(							-					) -				=					.
																																																	9
−∞														−1										3								4		3									−1										4							3					9				18
Находим ковариацию:																																																												y +1																		y +1
			+∞ +∞																																											1							0																		0				x	2
cov(ξ ,η ) = ∫					∫			xy × p(x, y)dxdy - M ξ × Mη =																∫∫				xy ×1dxdy - 0 ×(-																					) =				= ∫ dy ∫												xydx = ∫									( y ×				)dy =
			−∞		−∞																	с			ABC																	3											−1							− y −1											−1			2				− y −1
		0				( y +1)					2			(- y -1)	2
		= ∫ y ×(										-				)dy = 0
														2
			−1					2
Находим коэффициент корреляции																r =		cov(ξ ,η )								= 0
		Скачано																		Dξ × Dη

.	ru
Ч _ 2 _ 31_ 25

Используя неравенствоЧебышева, оценитьвероятностьтого, чтослучайная величинаξ отклонится отсвоего математическогоожидания M ξ менеечем

antiGTU

на Nσ , гдеσ = Dξ - среднеквадратическое отклонениеслучайной величиныξ ;

N - номер варианта

НеравенствоЧебышева:

P (

x - M ξ

< ε ) ³1 -

Dξ

Находим:

ε 2

P (

x - M ξ

< Nσ ) ³1 -

Dξ

=1

-

Dξ

=1 -

Dξ

=

N 2 -1

( Nσ )2

N 2σ 2

N 2 (

)2

N 2

-

Dξ

N = 25 P (

x - M ξ

< Nσ )

=

N 2

1

=

624

»1

2

N

625

Скачано

с

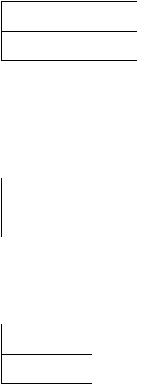
Ч_2_32_25

Cлучайная величина ξi

с одинаковой вероятностью может принимать одно из двух

значений:

iα

или

-iα .

Выяснить, удовлетворяет ли последовательность ξ ,ξ

2

, ...,ξ

, ... попарно

1

i

независимых

случайных величин закону больших чисел

.

1

n

1

n

lim P

∑ξi -

∑M ξi

< ε

= 1,

ε > 0 .

(1)

n

n

x→∞

i =1

i=1

antiGTU

Решить задачу для двух значений параметра

α :

α1 = -13,

α

2 = 0 49

Решение.

ξ1 ,ξ2 , ..., ξi , ... ruпопарно

Теорема

Чебышева утверждает:

если случайные величины

независимы и Dξi

£ c ,

i =1, 2, ... ,

где

c - некоторая

постоянная, то при любом ε > 0 выпол-

няется соотношение (1).

При этом предполагается, что величины ξi

имеют конечные матема-

тические ожидания

Mξi .

В данной

задаче по условию величины

ξi попарно независимы.

Найдем математические

ожидания

Mξi .

Закон

распределения величины

ξi

имеет вид:

ξi

iα

-iα

p

0.5

0.5

Поэтому

M ξ

i

= x p

+ x p

2

= iα

×0.5 - iα ×0.5 = 0;

значит, каждая случайная величина имеет конеч-

1

1

2

ное математическое ожидание (равное нулю).

Проверим, выполняется ли требование равномерной ограниченности дисперсий.

Напишем закон распределения

ξ 2

:

i

ξi

i2α

(-i )2

p

0.5

с

0.5

Или, сложив вероятности одинаковых возможных значений

Скачано

ξ

2

i2α

i

p

1

Дисперсия рав а Dξi = M (ξi

2 ) - (Mξi )2 = i2α ×1- 02 = i2α

1)

при

α

= - 13

имеем:

M

ξ

=

0,

Dξ

=

i−26

=

1

.

Т .к. i -

натуральное

число, то

1

i

i

i26

i26 ³ 1

и Dξ

i

£ 1 = c .

Зна ит,

при

α

= - 13 условия теоремы Чебышева выполняются,

1

и равенство

(1)

верное.

2)

при

α2 = 0.49

имеем:

M ξi = 0,

Dξi

= i0.98 .

Т.к.

i

- натуральное число,

то неравенство

i0.98

£ c

при всех

i

выполняться не

может.

Значит,

равенство (1) не

выполняется.

Oтвет:

при α1 = - 13 величины ξi

удовлетворяют закону больших чисел, а при

α2 = 0.49 - нет.

Ч _ 2 _ 33 _ 25			.	ru
На отрезке[0,α ] случайным образом выбраны n чисел, точнее,
рассматриваются n независимых случайных величинξ1 ,ξ2 ,...,ξn ,
равномерно распределенных на отрезке[0, α ]. Найти вероятность того,
antiGTU
	n
чтоих сумма заключена между x1 и x2 , те. . P x1	< ∑ξi	< x2
	i=1

Так как случайныевеличины распределены равномерно, то для каждой из них

M ξi	=	0 + α	= α
	2			2
Dξi	= (α - 0)2			= α 2
	12			12
								n
Значит для случайной величиныη = ∑ξi имеем
								i =1
Mη = n × M ξi =					n ×α	и Dη = n × Dξi	=	n ×α 2
				2			12

Тогда согласноцентральной предельной теореме, для одинаково распределенных случайных слагаемыхимеем

x - Mη

x - Mη

P ( x1 < η < x2 ) = F

2

- F

1

Dη

Dη

α = 3 /11

с

n = 1452

x1

= 192

x2

= 207

n ×α

1452 × 3 /11

Mη =

=

= 198

2

2

Dη =

n ×α 2

=

1452 × (3 /11)2

= 9

12

12

x - Mη

x

- Mη

207

-

198

192

-

198

P ( x1 < η < x2 ) = F

2

- F

1

= F

- F

=

Dη

Dη

9

9

= F (1) - F (-0.67) = F (1) + F (0.67)

По таблице II найдем F

P

= F (1) + F (0.67)

= 0.34134 + 0.24857 = 0.58991

Скачано

Ч_2_34_25

				am		ru
Известно, что случайная величина ξ имеет распределениеПуассона P(ξ = m) =				m!		e− a ,
неизвестным является параметр a . Используя метод максимальногоправдоподобия,
найтипо реализации выборки (x , x , ... , x ) значения оценки a				.
			неизвестного параметра а.
1	2	8
x1 = 35, x2 = 53, x3 = 43, x4 = 35, x5	= 34, x6 = 44, x7 = 37, x8 = 30
Решение.		antiGTU

Пустьξ - дискретная случайная величина с распределением P(ξ = am ) = pm = pm (a) ,

где m = 1, 2,..., am - возможные значения случайной величиныξ , pm (a) - соответствующие

k

вероятности , зависящиеот неизвестногопараметра а, причем ∑ pm (a) = 1

m=1

при любом допустимом а. Функцией правдоподобия называетсяфункцияпараметра а: L ( x1 ,..., xk ; a) = p1 (a) × p2 (a) ×... × pk (a ) . Величина a* , прикоторомфункция L ( x1 ,..., xk ; a)

достигнет максимума , является оценкоймаксимального правдоподобия неизвестного параметра а.

Составимфункциюправдоподобия:

L = (

ax1

× e− a )(

ax2

× e−a ) ×... × (

ax8

× e−a ) = e−8a ×

ax1 + x2 + ... + x8

x1 !x2 !×... × x8 !

x1 !

x2 !

x8 !

Находим производную и приравниваем еек нулю:

dL

=

1

(-8e−8a × ax1 + x2 + ... + x8

+ e−8a × (x

+ x

+ ...

+ x ) × ax1 + x2 + ... + x8 −1 ) =

da

x1 !× x2 !×... × x8 !

1

2

8

e−8a

× ax1 + x2 + ... + x8 −1

x1 + x2

+ ... + x8

=

(-8a + x1 + x2

+ ... + x8 ) = 0 -8

+ x1 + x2

+ ... + x8

= 0 a =

= x

8

x1 !× x2 !×... × x8 !

с

Т.о. а равна выборочнойсредней

x

: a = =

x

Находим вторую производную:

d

2

L

=

1

(-8e−8a × ax1 + x2 + ... + x8 −1 × (-8a + x + x

+ ... + x ) +

!× x2 !×

da2

x1

... × x8 !

1

2

8

Скачано

+ x8 ) + e−8a × ax1 + x2 + ... + x8 −1 × (-8)) =

+e−8a ×

(x1 + x2

+ ... + x8

-1)ax1 + x2 + ... + x8 −2 (-8a + x1 + x2

+ ...

e

−8a

× a

x1 + x2 + ... + x8 −2

=

(-8a(-8a + x + x

+ ... + x ) + (x + x

+ ... + x -1)(-8a + x + x

+ ... + x ) - 8a)

2

x1 !× x2 !×... ×

x8 !

1

2

8

1

8

1

2

8

При

a =

=

1

(x1 + x2

+ ... + x8 )

получаем:

x

8

d 2 L

e−8a × a8

−2

e−8a × a8

−2

x

x

=

× (-8a × (-8a + 8

x

) + (8

x

-1)(-8a + 8

x

) - 8a) =

× (-8a) < 0

x1 !× x2 !×

x1 !×

da2

... × x8 !

x2 !×... × x8 !

Вторая производная отриц тельн , значит, точка a =

есть точка максимума.

x

Вывод: a = a

=

. Витоге a =

1

(35 + 53 + 43 + 35 + 34 + 44 + 37 + 30) =

311

= 38.875

x

8

8

Находим математическое ожидание:

_

его к выборочной средней: Mξ = x .

Ч_2_35_25

Изветно, что случайная величинаξ имеет биномиальное распределение P (ξ = m) = Cnm pm (1 - p)n−m ,

неизвестным является параметр р. Используя метод моментов, найтипо реализациивыборки

( x , x ,..., x				) значениеоценки p* неизвестного параметра					р.		ru
1	2	8
x1 = 35,		x2		= 53, x3 = 43, x4 = 35, x5 = 34, x6 = 44, x7					= 37, x8 = 30.
n = 60.
Решение.
Согласно методу моментов следует найти математическоеожидание M										ξ величины.ξ и приравнять
								antiGTU

cогласнобиномиальному законупроизводится n независимых испытаний, в каждом из которых вероятностьпоявлениянекотрого события А равна p . Случайная велчина ξ представляет собой

число появлениясобытия А в n испытаниях. Обозначимξ1 - числопоявления события в первом испытании, ξ2 - вовтором, ..., ξn - в n-ом. Тогда ξ = ξ1 + ξ2 + ξn , причем дляξk , k =1,..., n имеем:

ξk	0	1
p	1 - p	p

Получаем:

согласносвойству математического ожидания:

M ξ = M (ξ1 + ξ2 + ... + ξn ) = M ξ1 + M ξ2 + ... + M ξn = × M ξk = × (0 × (1 - p) +1× p) = n × p

Согласно методу моментов приравниваем математическоеожиданиек выборочной средней:

_

		_	_
M ξ = x np* = x p* = x , где
					n
p* =	1	( x1	+ x2 + ... + xn ) =		1	(35 + 53 + 43 + 35 + 34 + 44 + 37 + 30) =		311	= 0.6479
	n				× 60			8 × 60
			8				с
			Скачано

Ч _ 2 _ 36 _ 25				ru
Случайная величинаξ имеет нормальное распределениес неизвестным
математическиможиданием a и известной дисперсиейσ 2			.
			. Повыборке
1		n
antiGTU			= a * Определить
(x1 , x2 ,..., xn ) объема n вычисленовыборочное среднее		∑ xi

n i=1

доверительный интервал для неизвестного параметра распределения a,

отвечающий заданной доверительной вероятности P.

a* =110 n =150 σ 2 =100

P = 0.98

Доверительный интервал для математическогоожидания a нормальной случайной величины при известной дисперсииσ 2 имеетвид:

- u ×

σ

< a <

+ u ×

σ

x

x

P

P

n

n

с

Из таблицыV находим

uP=0,98 = 2,326

Скачано

u ×

σ

= 2,326 ×

10

=1,9

P

150

n

доверительный интервал

a * -u ×

σ

< a < a * +uP

×

σ

P

n

n

110 -1,9 < a <110 +1,9

108,1 < a <111,9

Ч _ 2 _ 37 _ 25	ru

Случайная величинаξ имеет нормальное распределениес неизвестным математическиможиданием a и диспервиейσ 2 .

	Повыборке ( x1 , x2			,..., xn )	объема n вычисленыоценки a* =	1	n
							∑ xi и
						n i=1
	(σ 2 )* =	1	n		неизвестных параметров. Найти доверительный.
			∑( xi	- a *)2
		n -1 i=1
	интервалдля дисперсии при доверительной вероятности P
	a* = 2.1				antiGTU
	(σ 2 )* = 0.5

n = 31

P = 0.98

доверительный интервалоя для оценки математического ожижания a

нормального распределения при неизвестной дисперсииσ 2 :

a * -tP	× σ	*	< a < a * +tP	× σ	*
					n
		n

Из таблицыVI имеем tP=0.98 (k = n -1 = 30) = 2.457 Тогда

tP	× σ	*	= 2.457 ×		0.5		» 0.31	с
		n	31
Скачано

Искомый доверительный интервал: 2.1 - 0.31 < a < 2.1 + 0.31

1.79 < a < 2.41