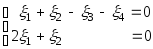- •Раздел 10 269
- •Раздел 10
- •§10.1. Определение и основные свойства
- •§10.2. Ортонормированный базис. Ортогонализация базиса
- •§10.3. Координатное представление скалярного произведения
- •§10.4. Ортогональные матрицы в евклидовом пространстве
- •§10.5. Ортогональные дополнения и ортогональные проекции в евклидовом пространстве
- •§10.6. Сопряженные операторы в евклидовом пространстве
- •§10.7. Самосопряженные операторы
- •§10.8. Ортогональные операторы
§10.5. Ортогональные дополнения и ортогональные проекции в евклидовом пространстве
Пусть в E задано некоторое подпространство E1. Рассмотрим множество E2E элементов x, ортогональных всем элементам из E1.
|
Определение 10.5.1. |
В
евклидовом пространстве E
совокупность элементов x
таких, что
|
|
Теорема 10.5.1. |
Ортогональное
дополнение
|
|
|
Доказательство:
Пусть
в E
Эта
однородная система линейных уравнений
(неизвестные в которой есть компоненты
элемента x),
определяющая ортогональное дополнение
E2
,
имеет ранг k
в силу линейной независимости элементов
Теорема доказана. |
Убедимся теперь в справедливости следующего утверждения.
|
Теорема 10.5.2. |
Если E2 ортогональное дополнение подпространства E1E, то E1 является ортогональным дополнением E2 . |
|
|
Доказательство:
Для
каждого элемента xE2
по условию следствия имеет место
равенство
Теорема доказана. |
|
Определение 10.5.2. |
В
евклидовом пространстве E
элемент y
называется ортогональной
проекцией
элемента x
на подпространство
1.
2.
|
|
Теорема 10.5.3. |
Если
|
|
|
Доказательство:
Если
в
Условие
Поскольку
основная матрица этой системы (как
матрица Грама набора линейно независимых
элементов
Теорема доказана. |
Отметим,
что если базис
![]() в подпространстве
в подпространстве![]() ортонормированный, то ортогональная
проекция элементаx
на
ортонормированный, то ортогональная
проекция элементаx
на
![]() есть элемент вида
есть элемент вида![]()
|
Задача 10.5.1. |
В
евклидовом пространстве
E
задает
подпространство
|
Решение:
1.
За базис подпространства
![]() можно взять пару элементов
можно взять пару элементов![]() и
и![]() ,
координатные столбцы которых образуют
фундаментальную систему решений для
,
координатные столбцы которых образуют
фундаментальную систему решений для
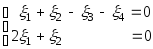 ,
,
например,
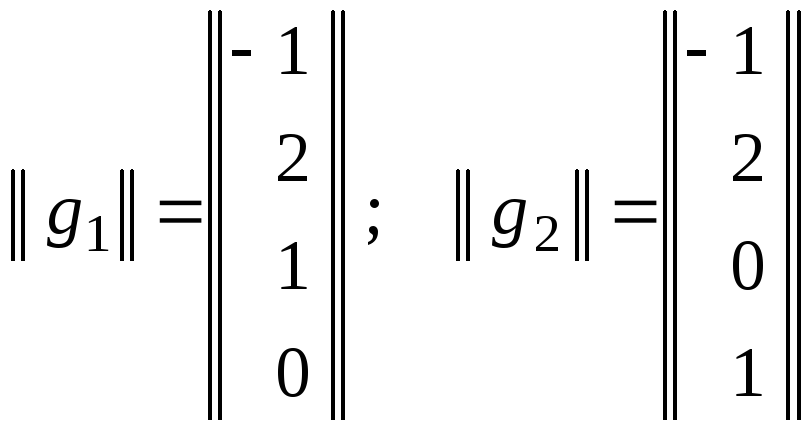 .
.
2.
Поскольку dim![]() =2,
то размерность ортогонального дополнения
=2,
то размерность ортогонального дополнения![]() согласно теореме 10.5.1. также равна 2. За
базис ортогонального дополнения
согласно теореме 10.5.1. также равна 2. За
базис ортогонального дополнения![]() удобно принять элементы
удобно принять элементы![]() и
и![]() такие, что
такие, что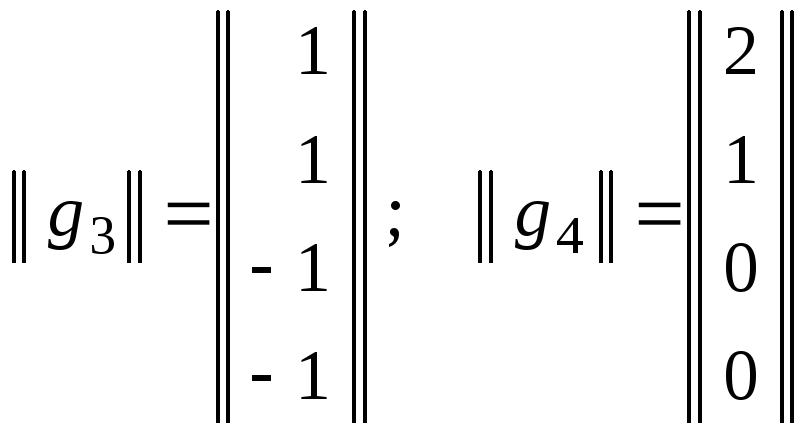 ,
поскольку они
,
поскольку они
- линейно независимы и
-
ортогональны каждому элементу из
подпространства
![]() ,
как образованные из коэффициентов,
заданной в условии задачи, системы
линейных уравнений.
,
как образованные из коэффициентов,
заданной в условии задачи, системы
линейных уравнений.
3.
Элементы
![]() ,
,![]() ,
,![]() и
и![]() линейно независимые по построению и
образуют базис вE
линейно независимые по построению и
образуют базис вE![]() .
Иначе говоря, каждый элемент из E
.
Иначе говоря, каждый элемент из E![]() может быть представлен, и притом
единственным образом, как линейная
комбинация элементов
может быть представлен, и притом
единственным образом, как линейная
комбинация элементов
![]() ,
,![]() ,
,![]() и
и![]() .
.
Откуда
следует, что искомый оператор
![]() - ортогонального проектирования элементовE
- ортогонального проектирования элементовE![]() на
на
![]() ,
должен удовлетворять соотношениям
,
должен удовлетворять соотношениям
![]()
В координатном представлении эти равенства можно переписать в виде
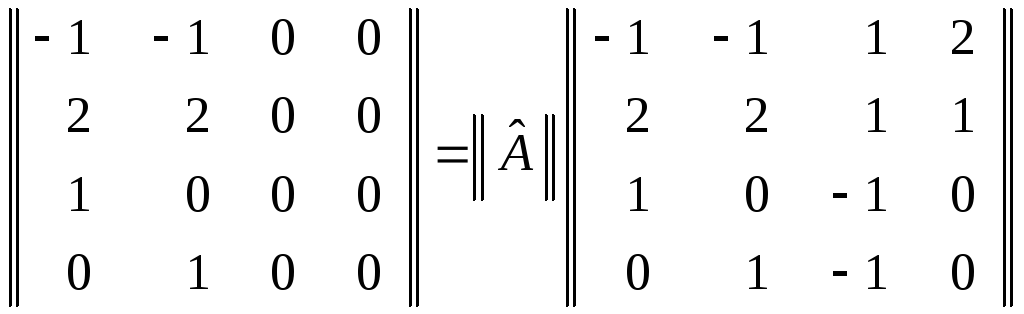 ,
,
и окончательно, воспользовавшись результатами §6.8., найдем, что
 .
.
Замечание: геометрическая интерпретация ортогонального проектирования вполне очевидна, однако эта операция используется и в других приложениях.
Например,
если E
есть евклидово пространство непрерывных
на
![]() функций со скалярным произведением
функций со скалярным произведением
![]() ,
,
а
![]() - подпространство алгебраических
многочленов
- подпространство алгебраических
многочленов![]() степени не выше, чемn
, то ортогональная проекция
степени не выше, чемn
, то ортогональная проекция
![]() - элементаE,
на
- элементаE,
на
![]() может рассматриваться как наилучшее
на
может рассматриваться как наилучшее
на![]() приближение
приближение![]() линейной комбинацией степенных
многочленов. Подробно эта задача
рассмотрена в §12.3.
линейной комбинацией степенных
многочленов. Подробно эта задача
рассмотрена в §12.3.

 ,
где
,
где
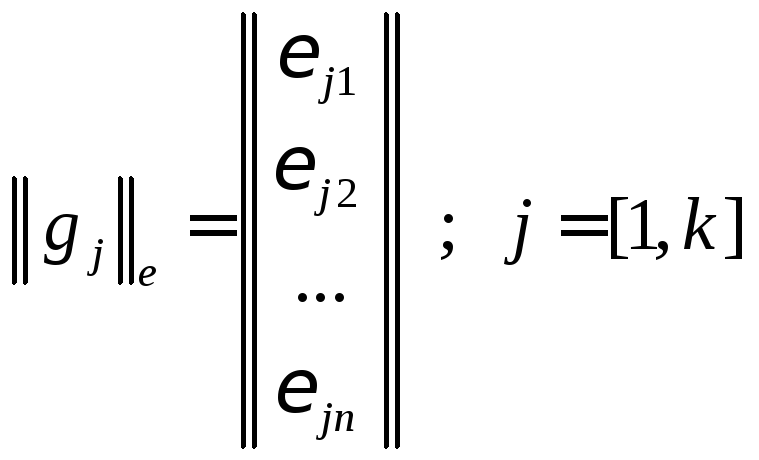 и
и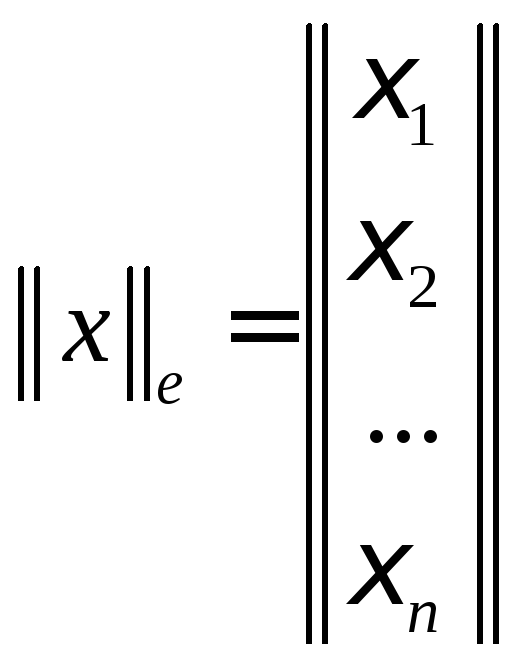 .
.