1. Само понятие множества строго не определяется(совокупность). Говоря о множествах, предполагается что они все «лежат» в универсальном множестве(Е). Если нет ни одного элемента, то пустое множество.

Принадлежность – не определена, принадлежность одного элемента множеству(xE). Пересечение: По опр: AB  xA => xB

По опр: A=B  AB & BA

Подмножество: Если АB, то А – подмножество множества В

а) объединение: AB; AB={xE|или xA, или xB, или xA и B одновременно|}

б) пересечение: AB; AB={xE|xA и xB одновременно|}

в) дополнение: A; A={xE|xA|}

дополнительно:

г) разность : A\B; A\B={xB|xA и xB|}; A\B=AB;

д) симметрическая разность: AB=(A\B)(B\A)

Круги Вейля:

Булева алгебра множеств:

Декартово произведение множеств: AxB={(x,y)|xA,yB|}

BxAAxB; |AxB|=|A|*|B|; |AxBxC|=|A|*|B|*|C|

2. Отображение множеств:

f: MN – называется отображением множества M в множество N, если xM – поставлено в соответствие по некоторому правилу элемент множества y=f(x)N

f:MN

а) f – инъективное (взаимно однозначное), если x1x2, M=> f(x1)f(x2).

b) f – сюръективное (отображение «на»), если yN, f-1(y)M.

c) f – биективно, если и инъективно и сюръективно.

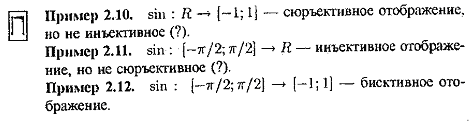
Кол-во элем декартова произведения множеств

4. Число всех отображений из X  Y.

5. Число инъективных и биективных отображений (X  Y).

X={x1,x2,..xm}, Y{y1,y2,..,yn}; In Y^X={f:xy|xixj => f(xi)f(xj)|}

тк все элементы f(x1),f(x2),..,f(xm)Y различны (f – инъективный отбор) => nm. При построении инъективных отображений xi переходит в элемент

Y: xi(y1,y2,..,yn) – n способов

x1yi; x2yj (yiyj) – (n-1) способов

…

x1yi; x2yj (yiyj), x3(y1,y2,..,yn), …, xm(n-m+1)

|In Y^X |= n(n-1)…(n-m+1)=n!/(n-m)!

если n=m, инъективное изображение будет биективным

|Bi Y^X| = n!

6. Множества с операциями. Определения и примеры группы (Zp и Sn)

Алгебраическая структура - это множество на котором определены некоторые операция для элементов.

М – определена бинарная операция «*», если для любых 2-х элементов поставлен в соответствии один элемент:  m,n  M => m*nM

1. Полугруппа – множество M с бинарной операцией «*» такой, что m,n,p  M => (m*n)*p = m*n*p – ассоциативный закон.

2. Группа – множество M с бинарной операцией «*», если M-полугруппа;  еМ – единичный(нейтральный) элемент => mM: me=em=m;

3. mM m^-1 такой что m*m^-1=e

При этом группа - Абелева группа, если m,nM=>m*n=n*m (операция коммутативна)

Пр: Рассмотрим множество целых чисел Z. Если это множество будем рассматривать с операцией сложения, то тогда вместе с этой операцией множество образует абелеву группу.

0) Z₁ + Z₂  Z  Z₁, Z₂

1) (Z₁ + Z₂) + Z₃ = Z₁ + (Z₂ + Z₃) – ассоциативно для  Z₁, Z₂, Z₃  Z

2) e = 0

3)  Z  Z^-1 = (-Z)

4) Z₁ + Z₂ = Z₂ + Z₁

Пр: Рассмотрим множество Z с операцией умножения {Z, .}

0) Z₁ ^. Z₂  Z  Z₁, Z₂

1) (Z₁ ^. Z₂) ^. Z₃ = Z₁ ^. (Z₂ ^. Z₃)

2)  e = 1 : Z ^. 1 = 1 ^. Z  Z => полугруппа с 1

Не будет образовывать группу, т.к. не  обратного элемента к Z

3)  2  Z, но не  2^-1  Z

Пр: Рассмотрим группу подстановок Sn (множество всех биекций XY (X=Y={1,..,n})

|Sn| = n!

1. (τ ρ) υ = τ (ρ υ)

2. e = (1,2,…,n; 1,2,…,n); eτ = τe = τ; τ

3. τ = (1,2,3); τ^-1 = (3,2,1); τ τ^-1, τ τ^-1 = τ^-1 τ = e

7. Определение кольца и поля, примеры (кольцо Zm и поле Zp – чем отличаются).

Кольцо – Это множество «K» с двумя операциями (сложения и умножения), которое удовлетворяет следующим условиям:

1. По сложению абелева группа;

2.  a,b,c  K => a(b+c) = ab+ac, (b+c)а = ba+ca дистрибутивность;

3. Операция умножения ассоциативна

3) а. Если операция умножения в кольце коммутативна, то К – коммутативное

ab=ba a, b  K => K – коммутативное кольцо

4. а. Если существует 1К по умножению, т.е. 1*а=а*1=а, то К с еденицей.

Пр: Zn – кольцо вычетов по |n|; Zn = {0,1,…,n-1}

i,j  Zn – рассмотрим операцию сложения в К Z и подправим её след. образом:

i+j= {k, k<n; k-n, k>n => n ≡ 0

Аналогично подправляем операцию умножения в К Z:

ij= ln(≡ 0) + k (0 ≤ k < n) => ij=k (ещё пример про делители 0 и т.п.)

Пр: {Z,+,*} – кольцо целых чисел (доказать, что кольцо, коммутативное, с 1 (4+3)).

Поле - Это множество «P» с двумя операциями (сложения и умножения), которое удовлетворяет следующим условиям:

1. P – коммутативное кольцо с единицей

2. x0P  x^-1 =>x^-1x=xx^-1=1 ;(те нет делителей нуля)

Пр: {R, Q, но не Z, +,*} – поле действительных чисел (xx0R x^-1=>x^-1x=xx^-1=1)

Теор: Zp – поле, если p – простое число

1. {Z₂, +, .} = {0,1} – поле; 10; (1)^-1=1

2. {Z₅, +, .} = {0,1,2,3,4} – поле; 2.3=1, 4.4=1, (1)^-1=1, (2)^-1=3, (3)^-1=2, (4)^-1=4 => 4²=1

8. Отношения на множестве. Отношение порядка (определения и примеры)

На множестве Х задано отношение , если:

1. определено некоторое подмножество (выделено) в декартовом произведении U XxX

2. xX находится в отношении , к элементу yX (и обозначается xy), если (x,y)U

Пр: xR, x<y (x,y)U

Типы отношений на множестве:

 - отношение, заданное на множестве Х

1)  - называют рефлексивным, если xx xX

2)  - называют транзитивным, если xy и yz => xz x,y,z X

3)  - называют симметричным, если xy => yx x,yX

4)  - называют антисимметричным, если xy => y не x x,yX

Отношение порядка – отношение  на множестве Х, если оно рефлексивно, транзитивно и антисимметрично

Пр:

1) {R, ≤}, ≤ - отношение порядка, т.к.:

- рефлексивно: x  R => x≤x

- транзитивно: x,y,z R => x≤y и y≤z => x≤z

- антисимметрично: x,yR => x≤y и y≤x => y=x

2) {R, <}, < - не отношение порядка, т.к. не выполняется рефлексивность

9. Отношения эквивалентности. Классы эквивалентности + теорема (с док-вом)

Отношение  на множестве X называется отношением эквивалентности если  - рефлексивно, транзитивно и симметрично.

[ Типы отношений на множестве:

 - отношение, заданное на множестве Х

1)  - называют рефлексивным, если xx xX

2)  - называют транзитивным, если xy и yz => xz x,y,z X

3)  - называют симметричным, если xy => yx x,yX

4)  - называют антисимметричным, если xy > yx x,yX ]

Пр: (R,=) – отношений эквивалентности

1. x => x=x - рефлексивно

2. x, y, z : x=y и y=z => x=z - транзитивно

3. x, y : x=y => y=x - симметрично

Пусть на множестве Х задано отношение эквивалентности. Тогда по определению классом эквивалентности хХ называется множество {yX | yx} = [x]_

Пр: (R, ); xy  |x|=|y|

[x]_ = {x, -x} – класс экв. состоит из 2-х эл-тов (их беск. много)

(можно ещё пример (N, ); mn  m-n = 3k (xZ) : [1], [2] и [3])

Т:  - отношение эквивалентности на Х

Тогда:

1. [x]    xX

2. x, y  X, если [x][y]  => [x]=[y]

(Если 2 класса пересекаются не по пустому множеству, то они совпадают)

3. 

Вывод:

Множество с отношением эквивалентности  раскладываются в объединения попарно непересекающихся классов эквивалентности, построенных по элементам этого множества.

Доказательство:

1. xX, [x] , т.к. x[x] (xx) из рефлективности отношений эквивалентности

2. z[x][y]. Пусть x1[x] и y1[y].

Мы хотим доказать что x1 и y1 находятся в отношении 

т.к. z[x] => x1z

т.к. z[y] => zy1 => из транзитивности x1y1, x1[x] и y1[y]

Т.к. мы выбираем произвольно то, можно взять y1=y => x1y, x1[x]  => [x][y]

Аналогично для y1[y] => y1x =>[y][x]

=> (из 2-х) [x] = [y]

3) (x) [x] => (x) {x}=X или (из тетр.) X= X (Возм только при рав-ве)

