4.5 Свойства выводимости из гипотез

[ВШ2, 2.1], [П1, 4.2], [Мен, 1.4], [Bil, 3–4]

Теорема 4.20 (монотонность). Если. . Г и. _ A, тоГ _ A.

(П1, теорема 4.2, с. 24.)

(Мен, с. 37.)

Доказательство. Теорема непосредственно следует из определений.

Теорема 4.21 (компактность). Если Г _ A, то существует такое конечное мно-

жество. . Г, что. _ A.

(П1, теорема 4.4, с. 25.)

(Мен, с. 37.)

Доказательство. Теорема непосредственно следует из определений.

Теорема 4.22 (транзитивность). Если Г _ A и для каждой формулы B . Г

имеет место. _ B , то. _ A.

18-24.

Алгебра Буля.

Выше отмечено: равносильности третьей группы говорят о том, что алгебра логики обладает коммутативными и ассоциативными законами относительно операций конъюнкции и дизъюнкции и дистрибутивным законом конъюнкции относительно дизъюнкции. Как известно, эти же законы имеют место и в алгебре чисел. Поэтому над формулами алгебры логики можно производить те же преобразования, которые проводятся в алгебре чисел: раскрытие скобок, заключение в скобки, вынесение за скобки общего множителя.

Но в алгебре логики возможны и другие преобразования, основанные на использовании, например, таких равносильностей:

(7) (16)

(П) (17)

(П) и т.д.

Эта особенность позволяет прийти к далеко идущим обобщениям.

Рассмотрим непустое множество М элементов любой природы: {x; y; z;…}, в котором определены отношение “=” (равно) и три операции: “+”( сложение), “·” ( умножение) и “-” (отрицание), подчиняющиеся следующим аксиомам:

Коммутативные законы:

1а. 1б.

Ассоциативные законы:

2а. . 2б..

Дистрибутивные законы:

3а. 3б..

Законы идемпотентности

4а. 4б.

Закон двойного отрицания:

5. .

Законы де Моргана:

6а. 6б..

Законы поглощения:

7а. . 7б..

Такое множество М называется БУЛЕВОЙ АЛГЕБРОЙ.

Если под основными элементами x,y,z,…подразумевать высказывания, под операциями “+”, “·”, “–“ дизъюнкцию, конъюнкцию, отрицание соответственно, а знак равенства рассматривать как знак равносильности, то, как следует из равносильностей рассмотренных выше трех групп, все аксиомы булевой алгебры выполняются.

В тех случаях, когда для некоторой системы аксиом удается подобрать конкретные объекты и конкретные соотношения между ними так, что все аксиомы выполняются, говорят, что найдена ИНТЕРПРЕТАЦИЯ ( ИЛИ МОДЕЛЬ) данной системы аксиом.

Значит, алгебра логики является интерпретацией булевой алгебры. Алгебра Буля имеет и другие интерпретации. Например, если под основными элементами x,y,z,…множества М подразумевать множества, под операциями “+”, “·”, “–“ объединение, пересечение, дополнение соответственно, а под знаком равенства – знак равенства множеств, то мы приходим к алгебре множеств. Нетрудно убедиться, что в алгебре множеств все аксиомы алгебры Буля выполняются.

Среди различных интерпретаций булевой алгебры имеются интерпретации и технического характера. Одна из них будет рассмотрена нами ниже. Как будет показано, она играет важную роль в автоматике.

Полные системы булевых функций

[П1, 3.1], [ВШ2, 1.2], [Мен, 1.3], [ЛМ, II.2], [КД, с. 43], [Гин, 6]

Определение 2.76. Если n . N, то n-местной булевой функцией называется

произвольная функция из множества {И,Л}n в множество {И,Л}.

(ВШ2, с. 12.)

2.77. Можно рассматривать формулы, использующие и другие пропозициональ-

ные связки (кроме ｬ, ., ., >), вводимые с помощью таблиц истинности.

Определение 2.78. Введём двуместные операции ., |, v, истинностные значения

которых определяются в соответствии со следующей таблицей.

A B A . B A | B A v B

Л Л Л И И

Л И И И Л

И Л И И Л

И И Л Л Л

Операция | называется штрихом Шеффера, операция v называется стрелкой Пирса.

Теорема 2.79.

1. A . B . ｬ(A-B) .

2. A | B . ｬ(A . B) .

3. A v B . ｬ(A . B) .

Упражнение 2.80. Сколько существует различных n-местных булевых функций?

Ответ 2.80. 22n.

Упражнение 2.81. Сколько существует различных 0-местных булевых функций?

Ответ 2.81. 2.

Определение 2.82. Введём 0-местные операции . и _, истинностные значения

которых определяются в соответствии со следующими таблицами.

Теорема 2.83.

1. A .ｬA . ..

12 20.10.2006

2. A .ｬA . _.

3. ｬ_ . ..

4. ｬ. . _.

5. A._ . A.

6. A.. . ..

7. A._ . _.

8. A.. . A.

Определение 2.84. Если зафиксирован конечный список, состоящий из n раз-

личных пропозициональных переменных, то каждая формула, содержащая только

переменные из данного списка, задаёт некоторую n-местную булеву функцию.

Пример 2.85. Рассмотрим список переменных P1, P2. Тогда формула ｬP2 . P1

задаёт следующую булеву функцию:

_Л,Л _> Л, _Л,И _> Л, _И,Л _> И, _И,И _> Л.

Определение 2.86. Пусть Ц — некоторое множество булевых функций. Систе-

ма Ц называется полной, если для каждого положительного n каждая n-местная

булева функция задаётся некоторой формулой, составленной из скобок, переменных

и обозначений операций из Ц.

Теорема 2.87. Система {., ., ｬ} полна.

(ВШ2, теорема 3, с. 18.)

Доказательство. Тождественно ложная функция задаётся формулой P1 . ｬP1.

Для остальных функций можно использовать доказательство теоремы 2.68.

(П1, с. 13.)

Пример 2.88. Система {., ｬ} полна, так как A . B . ｬ(ｬA .ｬB).

Пример 2.89. Система {>, .} полна, так как ｬA . A>. и A.B . (A>.).B.

Пример 2.90. Система {|} полна, так как ｬA . A | A и A . B . (A | A) | (B | B).

Пример 2.91. Система {v} полна, так как ｬA . A v A и A . B . (A v B) v (A v B).

Упражнение 2.92. Является ли полной система булевых функций {.,-, .}?

Ответ 2.92. Да. ｬA . A-., A . B . ｬ(ｬA . ｬB).

Выражение одних логических операций через другие

[П1, 3.1], [ЛМ, II.2]

Определение 2.93. Пусть Ц — некоторое множество булевых функций. Говорят,

что n-местная булева функция ψ выражается через функции из множества Ц, ес-

ли формула ψ(P1, . . . , Pn) равносильна некоторой формуле, составленной из скобок,

переменных и обозначений функций из Ц. Здесь P1, . . . , Pn — различные пропозици-

ональные переменные.

Упражнение 2.94. Можно ли выразить . через > и _?

Ответ 2.94. Нет. Из переменных P и Q и связок > и _ можно получить только 6 булевых

функций: _, P, Q, P >Q, Q>P, P . Q.

25-26.

В алгебре логики высказывания рассматриваются как нераздельные целые и только с точки зрения их истинности или ложности.

Ни структура высказываний, ни, тем более, их содержание не затрагиваются. В то же время и в науке, и в практике используются заключения, существенным образом зависящие как от структуры, так и от содержания используемых в них высказываний.

Например, в рассуждении “Всякий ромб – параллелограм; АВСD – ромб; следовательно, АВСD - параллелограм ” посылки и заключение являются элементарными высказываниями логики высказываний и с точки зрения этой логики рассматриваются как целые, неделимые, без учета их внутренней структуры. Следовательно, алгебра логики, будучи важной частью логики, оказывается недостаточной в анализе многих рассуждений.

В связи с этим возникает необходимость в расширении логики высказываний, в построении такой логической системы, средствами которой можно было бы исследовать структуру тех высказываний, которые в рамках логики высказываний рассматриваются как элементарные.

Такой логической системой является логика предикатов, содержащая всю логику высказываний в качестве своей части.

Логика предикатов, как и традиционная формальная логика, расчленяет элементарное высказывание на субъект (буквально – подлежащее, хотя оно может играть и роль дополнения) и предикат (буквально – сказуемое, хотя оно может играть и роль определения).

Субъект – это то, о чем что-то утверждается в высказывании;

предикат – это то, что утверждается о субъекте.

Например, в высказывании “7 - простое число”, “7” – субъект, “простое число” – предикат. Это высказывание утверждает, что “7” обладает свойством “быть простым числом”.

Если в рассмотренном примере заменить конкретное число 7 переменной х из множества натуральных чисел, то получим высказывательную форму “х – простое число”. При одних значения х (например, х=13, х=17) эта форма дает истинные высказывания, а при других значениях х (например, х=10, х=18) эта форма дает ложные высказывания.

Ясно, что эта высказывательная форма определяет функцию одной переменной х, определенной на множестве N, и принимающую значения из множества {1;0}. Здесь предикат становится функцией субъекта и выражает свойство субъекта.

Дадим несколько определений, относящихся к предикатам.

Определение 1.

Одноместным предикатом Р(x) называется произвольная функция переменного x, определенная на множестве M и принимающая значение из множества {1; 0}.

Множество М, на котором определен предикат Р(x), называется областью определения предиката Р(x).

Множество всех элементов , при которых предикат принимает значения “истина” (1), называется множеством (областью) истинности предиката Р(x), т.е. множество истинности предиката Р(х)- это множествоили иначе:или так:Так, например, предикат Р(x) – “x – простое число” определен на множестве N, а множество истинности I_P для него есть множество всех простых чисел.

Предикат Q(x) – “sinx=0” определен на множестве R, а его множеством истинности является

Предикат F(x) – “диагонали параллелограма x взаимно перпендикулярны” определен на множестве всех параллелограмов, а его множеством истинности является множество всех ромбов.

Из приведенных примеров видим, что одноместные предикаты выражают свойства предметов (субъектов).

Определение 2.

Предикат Р(х), определенный на множестве М, называется тождественно истинным, если его множество истинности совпадает с областью определения, т. е. I_p=M.

Определение 3.

Предикат Р(х), определенный на множестве М, называется тождественно ложным, если его множество истинности является пустым множеством, т. е. I_p=0.

Естественным обобщением понятия одноместного предиката является понятие многоместного предиката, с помощью которого выражаются отношения между предметами.

Примером бинарного отношения, т. е. отношения между двумя предметами, является отношение “меньше ”. Пусть это отношение введено на множестве Z целых чисел. Оно может быть охарактеризовано высказывательной формой “х<y”, где , то–есть является функцией двух переменных Р(х,y), определенной на множестве упорядоченных пар целых чисел ZхZ=Z² c множеством значений {1;0}.

Определение 4.

Двухместным предикатом Р(x,y) называется функция двух переменных x и y, определенная на множестве М=М₁хМ ₂ и принимающая значения из множества {1;0}.

В числе примеров двухместных предикатов можно назвать такие предикаты: Q(x, y) – “x=y” - предикат равенства, определенный на множестве RхR=R²; F(x,y) – “х параллелен y”, “прямая х параллельна прямой y”, определенный на множестве прямых, лежащих на данной плоскости.

Совершенно аналогично вводится понятие трехместного предиката. Приведем пример трехместного предиката (функции трех переменных): S(x,y,z) – “x+y=z”. Подстановка в него х=3 превращает его в двухместный предикат: S(y,z) – “3+y=z”, а подстановка х=3, z=2 – в одноместный предикат S(y) – “3+y=2”.Подстановка же S(2,3,5) превращает его в истинное высказывание, а S(1,7,4)– в ложное.

Аналогично определяется и n-местный предикат (функция n переменных). Пример п- местного предиката:

R(x₁, x₂,…,x_n): a₁ x₁+…+a_nx_n=0,

который, как видим, представляет собой алгебраическое уравнение с n неизвестными.

При n=0 будем иметь нульместный предикат – это логическая (пропозициональная) переменная, принимающая значения из множества {1;0}.

27.

Логические операции над предикатами.

Предикаты так же, как высказывания, могут принимать два значения: “истина” (1) и “ложь” (0), поэтому к ним применимы все операции логики высказываний, в результате чего из элементарных предикатов формируются сложные предикаты (как и в логике высказываний, где из элементарных высказываний формировались сложные, составные). Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов. Эти операции в логике предикатов сохраняют тот же смысл, который был им присвоен в логике высказываний.

Пусть на некотором множестве M определены два предиката P(x) и Q(x).

Определение 1.

Конъюнкцией двух предикатов P(x) и Q(x) называется новый (сложный) предикат , который принимает значение “истина” при тех и только тех значениях, при которых каждый из предикатов принимает значение “истина”, и принимает значение “ложь” во всех остальных случаях.

Очевидно, что областью истинности предиката является общая часть области истинности предикатов P(x) и Q(x), т.е. пересечение.

Так, например, для предикатов P(x): “x – четное число” и Q(x): “x кратно 3” конъюнкцией является предикат “x – четное число и x кратно трем”, т.е. предикат “x делится на 6”.

Определение 2.

Дизъюнкцией двух предикатов P(x) и Q(x) называется новый предикат , который принимает значение “ложь” при тех и только тех значениях, при которых каждый из предикатов принимает значение “ложь”, и принимает значение “истина” во всех остальных случаях.

Ясно, что областью истинности предиката является объединение области истинности предикатов P(x) и Q(x), т.е..

Определение 3.

Отрицанием предиката P(x) называется новый предикат или, который принимает значение “истина” при всех значениях, при которых предикат P(x) принимает значение “ложь”, и принимает значение “ложь” при тех значениях, при которых предикат P(x) принимает значение “истина”.

Очевидно, что , т.е. множество истинности предикатаявляется дополнением к множествуI_P.

Определение 4.

Импликацией предикатов P(x) и Q(x) называется новый предикат , который является ложным при тех и только тех значениях, при которых одновременно P(x) принимает значение “истина”, а Q(x) – значение “ложь”, и принимает значение “истина” во всех остальных случаях.

Поскольку при каждом фиксированном справедлива равносильность, то.

Определение 5.

Эквиваленцией предикатов P(x) и Q(x) называется новый предикат , который обращается в “истину” при всех тех и только тех, при которых P(x) и Q(x) обращаются оба в истинные или оба в ложные высказывания.

Для его множества истинности имеем:

28-29.

Кванторные операции.

Рассмотрим операции, преобразующие предикаты в высказывания.

Пусть имеется предикат Р(х) определенный на множестве М. Если “а” – некоторый элемент из множества М, то подстановка его вместо х в предикат Р(х) превращает этот предикат в высказывание Р(а). Такое высказывание называют единичным. Например, r(x): “х – четное число” – предикат, а r (6)- истинное высказывание, r (3) – ложное высказывание.

Это же относится и к n – местным предикатам: если вместо всех предметных переменных х_i, i=подставить их значения, то получим высказывание.

Наряду с образованием из предикатов высказываний в результате таких подстановок в логике предикатов рассматриваются еще две операции, которые превращают одноместный предикат в высказывание. Эти операции называются операциями квантификации (или просто квантификацией, или связыванием кванторами, или навешиванием кванторов). При этом рассматриваются, соответственно, два типа так называемых кванторов.

1. Квантор всеобщности.

Пусть Р(х) – предикат, определенный на множестве М. Под выражением понимаютвысказывание, истинное, когда Р(х) истинно для каждого элемента х из множества М, и ложное в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение звучит так: “Для всякого х Р(х) истинно ”.

Символ называютквантором всеобщности (общности). Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М), в высказывании же х называютсвязанной квантором всеобщности.

2. Квантор существования.

Пусть P(x) -предикат определенный на множестве М. Под выражением понимаютвысказывание, которое является истинным, если существует элемент , для которого P(x) истинно, и ложным – в противном случае. Это высказывание уже не зависит от x. Соответствующее ему словесное выражение звучит так: “Существует x, при котором P(x) истинно.” Символназываютквантором существования. В высказывании переменная x связана этим квантором (на нее навешен квантор).

Кванторные операции применяются и к многоместным предикатам. Пусть, например, на множестве М задан двухместный предикат P(x,y). Применение кванторной операции к предикату P(x,y) по переменной x ставит в соответствие двухместному предикату P(x,y) одноместный предикат (или одноместный предикат), зависящий от переменнойy и не зависящий от переменной x. К ним можно применить кванторные операции по переменной y, которые приведут уже к высказываниям следующих видов:

Рассмотрим предикат P(x) определенный на множестве M={a₁,…,a_n}, содержащем конечное число элементов. Если предикат P(x) является тождественно - истинным, то истинными будут высказывания P(a₁),P(a₂),…,P(a_n). При этом истинными будут высказывания и конъюнкция.

Если же хотя бы для одного элемента P(a_k)окажется ложным, то ложными будут высказывание и конъюнкция . Следовательно, справедлива равносильность .

Численные кванторы.

В математике часто встречаются выражения вида “по меньшей мере n” (“хотя бы n”), “не более чем n”, “n и только n” (“ровно n”), где n – натуральное число.

Эти выражения, называемые численными кванторами, имеют чисто логический смысл; они могут быть заменены равнозначными выражениями, не содержащими числительных и состоящими только из логических терминов и знакаили ~, означающего тождество (совпадение) объектов.

Пусть n=1. Предложение “По меньшей мере один объект обладает свойством P” имеет тот же смысл, что и предложение “Существует объект, обладающий свойством P”, т.е. (*)

Предложение “не более чем один объект обладает свойством P” равнозначно предложению “Если есть объекты, обладающие свойством P, то они совпадают”, т.е. (**) Предложение “один и только один объект обладает свойством P” равнозначно конъюнкции вышеуказанных предложений (*) и (**).

30.

Логический квадрат – это основная конструкция в силлогистике для изучения отношений по истинности между суждениями с одинаковыми терминами. Из логического квадрата видно лишь, что будет с истинностью остальных трех суждений, если зафиксировать истинностное значение одного из них, не более того; на каких же основаниях оно зафиксировано – это внелогический вопрос.

31-32.

Понятие формулы логики предикатов.

В логике предикатов будем пользоваться следующей символикой :

1. Символы p, q, r, …- переменные высказывания, принимающие два значения: 1- истина , 0 – ложь.

2. Предметные переменные – x, y, z, … , которые пробегают значения из некоторого множества М;

x⁰, y⁰, z⁰ – предметные константы, т. е. значения предметных переменных.

3. P(·), Q(·), F(·), … - одноместные предикатные переменные;

Q(·,·,…,·), R(·,·, …,·) – n-местные предикатные переменные.

P⁰(·), Q⁰(·,·, …,·) – символы постоянных предикатов.

4. Символы логических операций:

5. Символы кванторных операций:

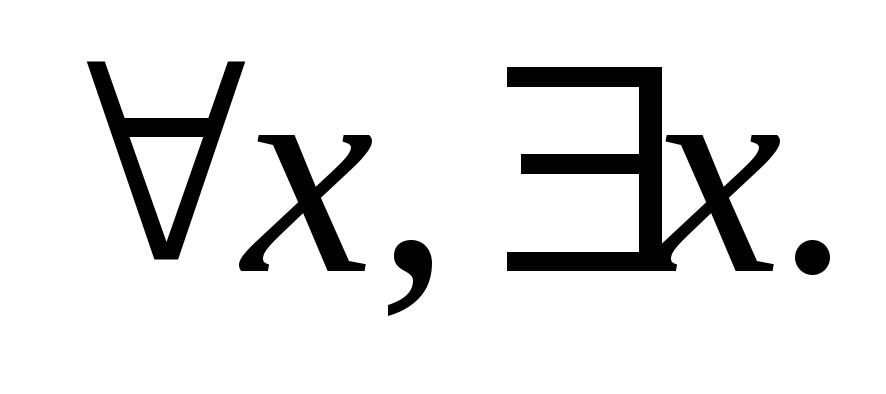
6. Вспомогательные символы: скобки, запятые.

Определение формулы логики предикатов.

1. Каждое высказывание как переменное, так и постоянное, является формулой (элементарной).

2. Если F(·,·, …,·) – n-местная предикатная переменная или постоянный предикат, а x₁, x₂,…, x_n– предметные переменные или предметные постоянные (не обязательно все различные), то F(x₁, x₂,…, x_n) есть формула. Такая формула называется элементарной, в ней предметные переменные являются свободными, не связанными кванторами.

3. Если А и В – формулы, причем, такие, что одна и та же предметная переменная не является в одной из них связанной, а в другой – свободной, то слова есть формулы. В этих формулах те переменные, которые в исходных формулах были свободны, являются свободными, а те, которые были связанными, являются связанными.

4. Если А – формула, то – формула, и характер предметных переменных при переходе от формулы А к формулене меняется.

5. Если А(х) – формула, в которую предметная переменная х входит свободно, то слова 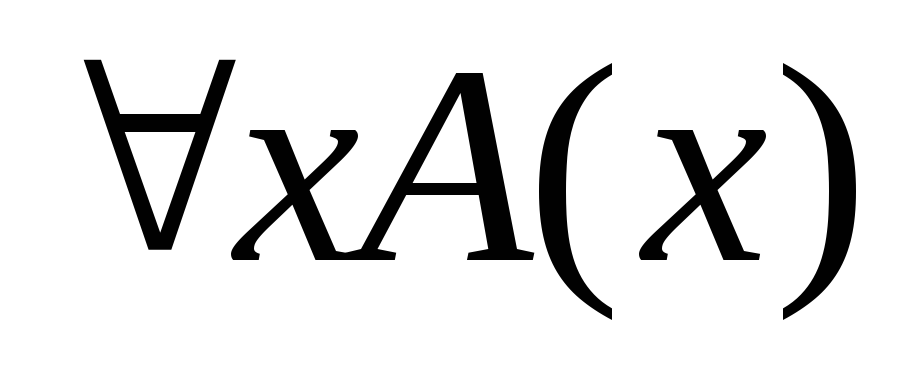иявляются формулами, причем, предметная переменная входит в них связанно.

6. Всякое слово, отличное от тех, которые названы формулами в пунктах 1 – 5, не является формулой.

Например, если Р(х) и Q(x,y) – одноместный и двухместный предикаты, а q, r – переменные высказывания, то формулами будут, например, слова (выражения):

.

Не является формулой, например, слово: . Здесь нарушено условие п.3, так как формулупеременная х входит связанно, а в формулу Р(х) переменная х входит свободно.

Из определения формулы логики предикатов ясно, что всякая формула алгебры высказываний является формулой логики предикатов.

33.

Равносильные формулы логики предикатов.

Определение 1.

Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.

Определение 2.

Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области.

Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей.

Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, не содержащая х). Тогда имеют место равносильности:

1.

2.

3.

4.

5.

6. .

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

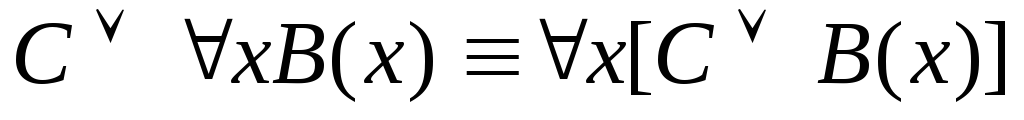
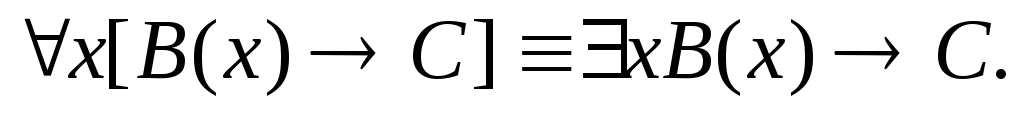
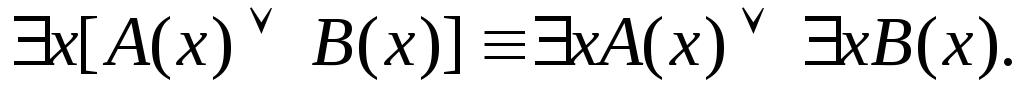
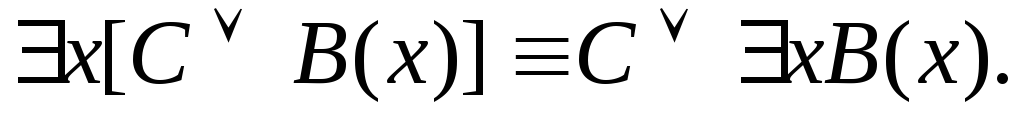
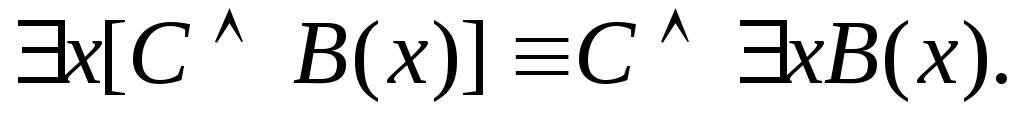
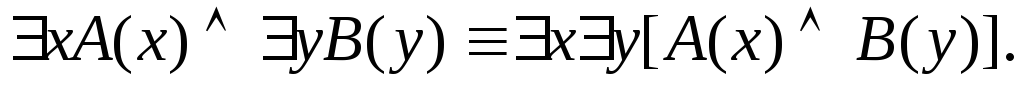
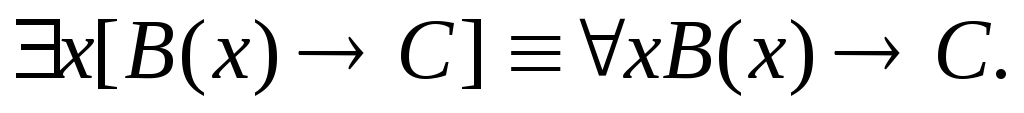
Равносильность 1 означает тот простой факт, что, если не для всех х истинно А(х), то существует х, при котором будет истиной .

Равносильность 2 означает тот простой факт, что, если не существует х, при котором истинно А(х), то для всех х будет истиной .

Равносильности 3 и 4 получаются из равносильностей 1 и 2, соответственно, если от обеих их частей взять отрицания и воспользоваться законом двойного отрицания.

ЗАКОНЫ ЛОГИЧЕСКИХ ОПЕРАЦИЙ.

(общезначимые формулы логики предикатов)

. . . . . . . . . . . . . . .

. . . . . . . . .

34.

Теорема компактности для логики предикатов

[УВП, 4.4], [ВШ2, 4.5], [БДж, 17], [ЛМ, II.6], [П1, 6.4], [КД, с. 213],

[Bil, 8, 9]

Теорема 5.15 (теорема Мальцева о компактности). ПустьA — замкнутая фор-

мула сигнатуры. иГ — некоторое множество замкнутых формул сигнатуры.. Если

Г _ A, то существует такое конечное множество. . Г, что. _ A.

(УВП, теорема 14, с. 88.)

(ВШ2, теорема 50, с. 185.)

Доказательство. Пусть Г _ A. Согласно теореме 5.14 Г _ A. Согласно теоре-

ме 5.8 существует такое конечное множество . . Г, что . _ A. Согласно теоре-

ме 5.11 . _ A.

Теорема 5.16 (локальная теорема Мальцева). ПустьГ — некоторое множество

замкнутых формул сигнатуры .. Если каждое конечное подмножество множестваГ

имеет модель, то и само множество Г имеет модель.

(УВП, теорема 13, с. 88.)

(ВШ2, теорема 50, с. 185.)

48 20.10.2006

Доказательство. Зафиксируем произвольную замкнутую формулу B сигнату-

ры .. Пусть множество Г не имеет ни одной модели. Тогда Г _ B . ｬB. Согласно

теореме 5.15 существует такое конечное множество . . Г, что . _ B . ｬB. Оче-

видно, множество . не имеет ни одной модели, что противоречит условию теоремы.

Поэтому Г имеет модель.

Теорема 5.17. Пусть T — некоторая теория первого порядка с равенством. Если

теория T имеет модель, то T имеет и нормальную модель.

(ВШ2, теорема 59, с. 203.)

Доказательство. Пусть M = _M,. является моделью теории T. Согласно опре-

делению теории первого порядка с равенством отношение =_ является отношением

эквивалентности (то есть оно рефлексивно, симметрично и транзитивно). Множе-

ство M разбивается на классы эквивалентности, множество этих классов обознача-

ется M/=_. Формально

(M/=_) = {A . M | A = {b . M | a =_ b} для некоторого a . M}.

На множество M/=_ можно стандартным образом перенести функции и предика-

ты из интерпретации M. Полученная интерпретация является нормальной моделью

теории T.

Теорема 5.18. Пусть T — некоторая теория первого порядка с равенством. Если

каждое конечное подмножество множества T имеет нормальную модель, то и сама

теория T имеет нормальную модель.

(УВП, теорема 13, с. 88.)

Доказательство. Теорема непосредственно следует из теорем 5.16 и 5.17.

35.

Нормальные формы формул логики предикатов.

В логике предикатов, как и в логике высказываний, формулы могут иметь нормальную форму, т.е. существуют эквивалентные нормальные формы представления любых предикатных формул. При этом, используя равносильности алгебры высказываний и логики предикатов, каждую формулу логики предикатов можно привести к нормальной форме. В логике предикатов различают два вида нормальных форм: приведенную и предваренную.

Определение.

Говорят, что формула логики предикатов имеет приведенную нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам.

Пример 1.

.

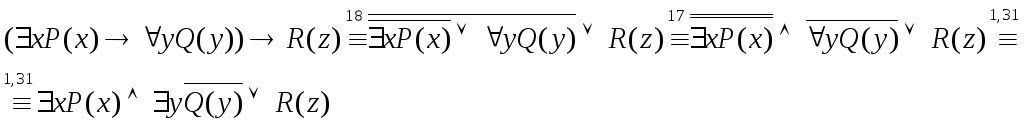Получили приведенную нормальную форму исходной формулы.

Среди нормальных форм формул логики предикатов выделяют так называемую предваренную (префиксную, пренексную) нормальную форму (ПНФ). В ней кванторные операции либо полностью отсутствуют, либо они используются после всех операций алгебры логики, т.е. ПНФ формулы логике предикатов имеет вид

,

где под символом понимается один из кванторовили, а формула А кванторов не содержит.

Процедура получения (приведения) ПНФ. Состоит в следующем:

1. Используя формулы 18, 19 (отнесенные к предикатам), заменить операции 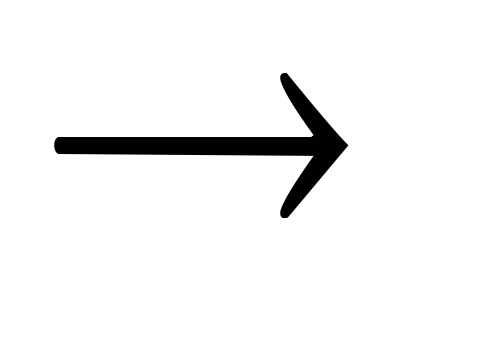и ~ на.

2. Используя формулы логики предикатов 31, 32, а также формулы логики высказываний 1, 16, 17, представить предикатную формулу таким образом, чтобы символы отрицания относились непосредственно к символам предикатов (и, таким образом, мы приводим исходную формулу к приведенной форме).

3. Для формул, содержащих подформулы вида , вести новые переменные, позволяющие использовать соотношения 46, 47, 49, 50 или 53, 54.

4. С помощью формул 35 – 38, 46, 47, 49, 50, 53, 54 получить формулу в виде ПНФ.

Пример 2.

обозначим в предикате Q переменную y через z

Пример 3.

обозначим в предикате Q переменную x через z

–ПНФ.

Пример 4.

последний предикат не зависит от переменной z

два первых предиката не зависят от переменной u - ПНФ.

Пример 5.

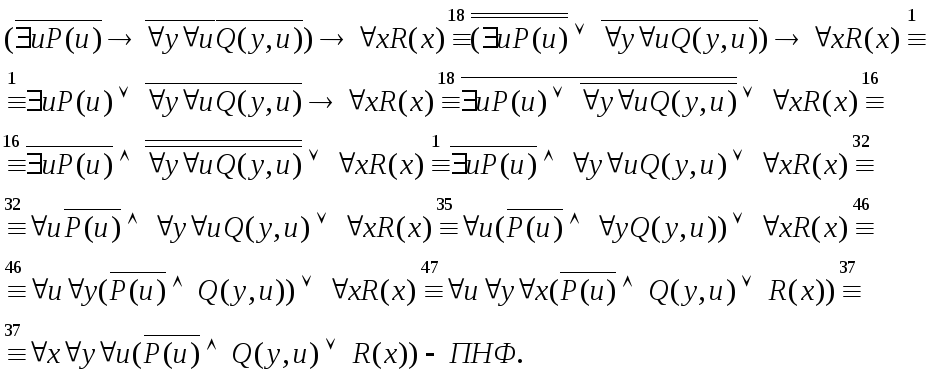
36.

Алгоритм — предписание выполнить точно определённую последователь-

ность действий.

С каждым алгоритмом связаны область возможных исходных данных X и об-

ласть возможных значений Y . При этом алгоритм вычисляет некоторую частичную

функцию f : X > Y . Процесс применения алгоритма A к исходному данному x . X

всегда происходит по шагам. Каждый шаг обязательно заканчивается. Процесс при-

менения алгоритма A к x либо будет продолжаться бесконечно, либо остановится

после конечного числа шагов с результатом, либо остановится без результата.

Вк ачестве области возможных исходных данных и области возможных значений

обычно используют множества вида Nk или У., где У — конечный алфавит (эти

множества — примеры ансамблей конструктивных объектов).

50 20.10.2006

Определение 6.8 (область применимости/результативности алгоритма). Об-

ласть применимости алгоритма A состоит из тех данных, при применении к кото-

рым алгоритма A процесс остановится с результатом.

6.9. Вм атематике уточнения понятия алгоритма называются вычислительны-

ми моделями. Наиболее известные вычислительные модели: машины Тьюринга, ча-

стично рекурсивные функции, машины с неограниченными регистрами, нормальные

алгорифмы Маркова, канонические системы Поста, лямбда-исчисление.

37.

6.10. Образно говоря, детерминированная машина Тьюринга имеет бесконеч-

ную в обе стороны ленту, разделённую на ячейки. Вкаж дой ячейке может быть за-

писан любой символ из конечного алфавита, называемого рабочим алфавитом (или

ленточным алфавитом) данной машины Тьюринга. Имеется управляющее устрой-

ство. Оно может находиться в одном из конечного множества состояний. Имеется

одна читающе-записывающая головка, которая в каждый момент обозревает одну

из ячеек ленты. Один такт работы состоит в следующем: машина читает символ

в обозреваемой ячейке, выбирает из своей программы инструкцию, соответствую-

щую текущему состоянию и прочитанному символу, и исполняет её. Вин струкции

сказано, какой символ следует записать в обозреваемую ячейку, каким будет новое

состояние управляющего устройства и куда должна переместиться головка (на од-

ну ячейку влево, на одну ячейку вправо или остаться на месте). Эти перемещения

принято обозначать L, R и N соответственно (в некоторых учебниках вместо букв

используют числа .1, 1 и 0).

Вм ножестве состояний выделены два состояния — начальное (q1) и заключи-

тельное (q0). Попав в заключительное состояние машина останавливается. Один из

символов рабочего алфавита выделен и называется бланком (или пробелом). Снача-

ла почти вся лента заполнена бланками (только конечное число ячеек ленты может

содержать символы, отличные от бланка).

(УВП, с. 109–110.)

Определение 6.11. Детерминированная машина Тьюринга (или просто машина

Тьюринга) — это набор M = _Q,У, a0, δ, q1, q0, где Q и У — конечные множества,

a0 . У, q1 . Q, q0 . Q и δ: (Q_{q0}).У) > (Q.У.{L,N,R}). Здесь Q — множество

состояний, У — ленточный алфавит, a0 — бланк (пробел, пустой символ), δ —

таблица переходов, q1 — начальное состояние, q0 — заключительное состояние.

6.12. Для удобства будем обозначать бланк символом # (в некоторых учебниках

используют символ или _).

6.13. Функцию δ принято записывать в виде множества команд P. Если

δ_q, a = _r, b, к, то этому соответствует команда qa > rbк (в некоторых учебниках

пишут qa > bкr). Вуп ражнениях команды вида qa > qaN можно не записывать.

Пример 6.14. Пример машины Тьюринга: q1# > q21L, q2# > q01L.

Определение 6.15. Вк аждый момент имеется некоторая конфигурация, скла-

дывающаяся из содержимого ленты, положения головки и состояния управляющего

устройства. Мы будем записывать конфигурацию в виде слова uqav, где q — текущее

51 20.10.2006

состояние, a — символ в обозреваемой ячейке, u — слово, записанное на ленте левее

обозреваемой ячейки, v — слово, записанное на ленте правее обозреваемой ячейки.

При этом все остальные ячейки (левее слова u и правее слова v) содержат только

бланки.

(УВП, с. 111.)

Определение 6.16. Пусть У0 . У и # /. У0. Пусть f — частичная функция из У.0

в У.0

. Машина Тьюринга M = _Q,У,#, δ, q1, q0 вычисляет функцию f, если для

каждого слова x . У.0

выполнены следующие условия.

1. Начав работу с конфигурации q1#x, машинаMостанавливается в том и только

в том случае, если функция f определена на входе x.

2. Если машина M остановилась, начав работу с конфигурации q1#x, то заклю-

чительной конфигурацией является q0#y, где f(x) = y.

Вн екоторых учебниках такое определение вычисления называется «вычислением

в сильном смысле» или «правильным вычислением».

(П2, с. 3.)

(ЛМ, с. 137.)

Определение 6.17. Пусть 1 . У и 1 _= #. Пусть f — частичная функция из N в N.

Машина Тьюринга M= _Q,У,#, δ, q1, q0 вычисляет функцию f, если для каждого

числа n . N выполнены следующие условия.

1. Начав работу с конфигурации q1#1n, машина M останавливается в том и

только в том случае, если функция f определена на входе n.

2. Если машина M остановилась, начав работу с конфигурации q1#1n, то заклю-

чительной конфигурацией является q0#1f(n).

(П2, с. 3.)

(УВП, с. 118.)

Пример 6.18. Машина Тьюринга из примера 6.14 вычисляет функцию f : N > N,

заданную формулой f(x) = x + 2.

Упражнение 6.19. Функция sg: N > N задаётся формулой

sg(x) = _0, если x = 0,

1, если x > 0.

Построить машину Тьюринга, вычисляющую функцию sg.

Упражнение 6.20. Функция sg: N > N задаётся формулой

sg(x) = _1, если x = 0,

0, если x > 0.

Построить машину Тьюринга, вычисляющую функцию sg.

Определение 6.21. Пусть 1 . У и 1 _= #. Пусть f — частичная функция из Nk

в Nm. Машина Тьюринга M = _Q,У,#, δ, q1, q0 вычисляет функцию f, если для

каждого кортежа _n1, n2, . . . , nk . Nk выполнены следующие условия.

1. Начав работу с конфигурации q1#1n1#1n2#. . .#1nk, машина M останавли-

вается в том и только в том случае, если функция f определена на вхо-

де _n1, n2, . . . , nk.

38.