3.Задача коммивояжера

1. Постановка задачи

Имеется городов, занумерованных числами от 1 до. Расстояния между любой парой городов известны и состаляют. Если между городамиинет дороги, то. По тем же соображениям. Вообще говоря,(путь в одну сторону не обязательно совпадает с путем, пройденным в обратную сторону). Коммивояжер (бродячий торговец), выезжая из какого-либо города, должен посетить все города, побывав в каждом ровно один раз, и вернуться в исходный город. Объезд городов, удовлетворяющий этим требованиям, называетсямаршрутом коммивояжера. Под длиной машрута понимается сумма длин всех входящих в него переездов из города в город.

Необходимо определить маршрут минимальной длины.

2. Метод ветвей и границ

Метод ветвей и границ [3,4,5] относится к группе комбинаторных методов дискретного программирования. Методы этой группы исходят прежде всего из конечности множества допустимых решений задачи. Центральную идею комбинаторных методов составляет замена полного перебора всех допустимых решений их частичным напрвленным перебором. Впервые метод ветвей и границ был предложен в 1960 г. в работе Лэнд и Дойг для решения задачи целочисленного линейного программирования. Настоящую известность этот метод приобрел лишь после выхода в 1963 г. работы Литтла и др., в которой метод был применен к задаче коммивояжера. В этой работе было впервые предложено и общепринятое теперь название метода.

Различные методы типа ветвей и границ существенно используют специфику конкретных задач и поэтому заметно отличаются друг от друга. Однако все они основаны на последовательном разбиении допутимого множества на подмножества (ветвелении) и вычислении оценок (границ), позволяющем отбрасывать подмножества, заведомо не содержащие оптимальных решений задачи. Изложим идею метода ветвей и границ для следующей комбинаторной задачи:

(16)

где - конечное множество.

Пусть есть подмножество. В зависимости от специфики задачи выбирается некоторый способ вычислениянижней границы (оценки) значений целевой функции , т.е. такого числа, что для любогоимеет место неравенство

(17)

По некоторому правилу множество разбивается на конечное число (обычно попарно непересекающихся) полнможеств. Получается начальное дерево ветвления с корнеми листьями (висячими вершинами)(рис. 4).

Множество для дальнейшего ветвления выбирается по определенному правилу среди множеств . Обычно это подмножество с наименьшей оценкой, так как именно в неи естественно искать оптимальное решение в первую очередь. Далее для подмножеств, полученных после разбиения выбранного множества, вычисляется множество, еще не подвергавшееся разбиению, т.е. множество, которое соответствует висячей вершине дерева ветвления.

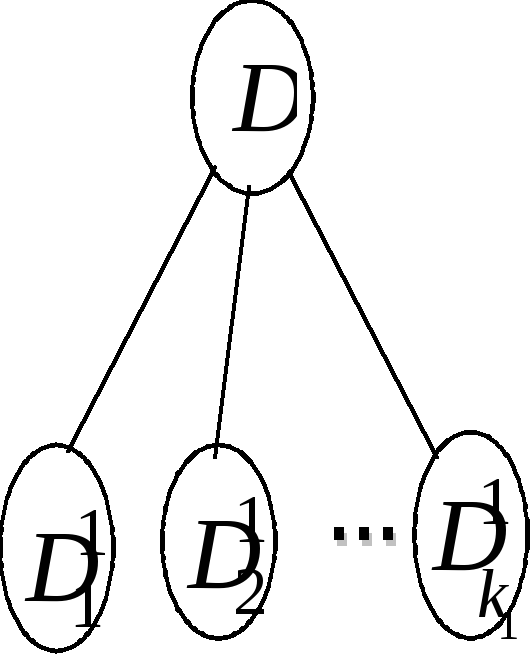
Рис. 4

Через некоторое число шагов в результате разбиения очередного подмножества или в ходе вычисления оценки для одного из подмножеств будет получено - допустимое решение исходной задачи. Значениеобъявляется рекордом целевой функции,. Если для любого подмножества, для которого еще не выполнялось ветвление, имеет место соотношение

, (18)

то - оптимальное решение задачи (16) и процесс решения завершается. Иначе решение задачи продолжается с некоторого подмножества, для которого (18) не выполняется. При этом подмножества, для которых (18) имеет место, объявляются неперспективными и исключаются из последующего рассмотрения.

В дальнейшем при получении допустимого решения, на котором значение целевой функции меньше , рекорд обновляется. Оптимальным решением задачи является лучшее из найденных решений.