4.3. Теоремы двойственности

Двойственность является одним из фундаментальных понятий в теории ЛП. Исключительно важную роль играют следующие утверждения, получившие названия теорем двойственности [1,3].

Первая теорема двойственности. Если одна из пары двойственных задач (I) и (II) разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают:

где – оптимальные планы задач (I) и (II) соответственно.

Говорят, что допустимые решения x,yудовлетворяют условиям дополняющей нежесткости (УДН), если при подстановке этих векторов в ограничения задач (I) и (II) хотя бы одно из любой пары сопряженных неравенств обращается в равенство.

Вторая теорема двойственности.оптимальны в задачах (I) и (II) тогда и только тогда, когда они удовлетворяют УДН.

4.4. Пример

Используя теоремы двойственности решить двойственную задачу, если известно решение прямой задачи.

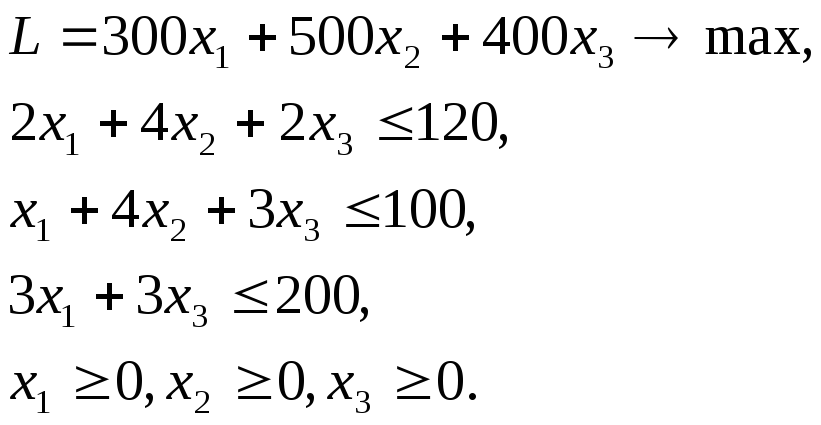(20)

Пусть решение задачи найдено одним из стандартных методов: . Построим двойственную задачу:

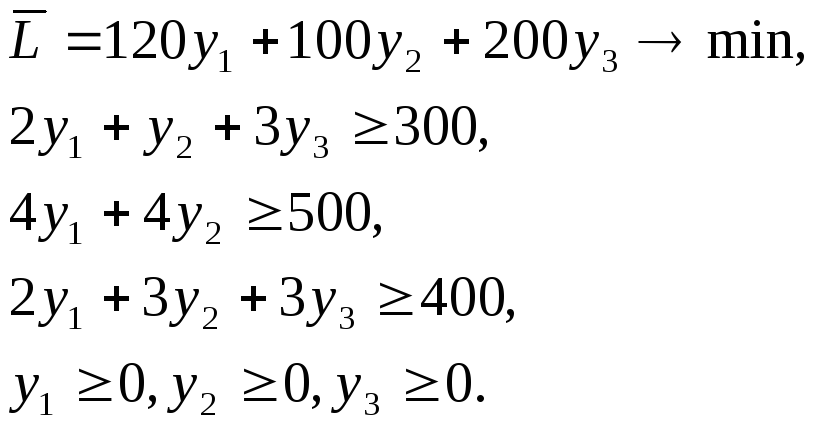(21)

По первой теореме двойственности задача разрешима, причем . Найдем оптимальный план задачи (21), используя вторую теорему двойственности. Подставим координаты векторав ограничения задачи (20). Получим

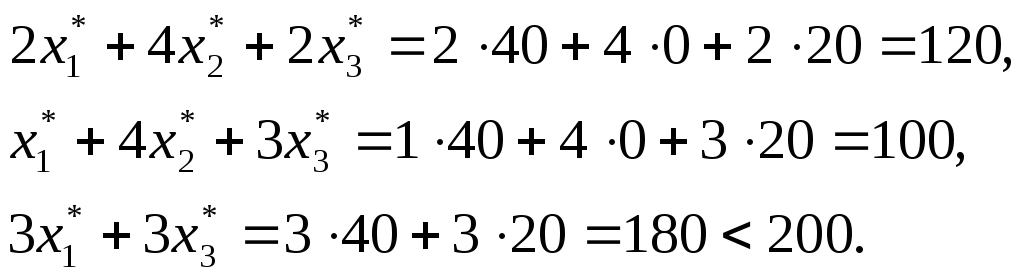
Следовательно, в силу УДН, неравенство должно выполняться как равенство, т.е.. Далее так как, то в силу УДН,

Получаем систему линейных уравнений и решаем ее:

Планы иудовлетворяют УДН, следовательно, в силу второй теоремы двойственности, являются оптимальными в задачах (20) и (21) соответственно.

4.5. Пример

Исследовать вектор на оптимальность в задаче ЛП.

Вначале нужно проверить, является ли вектор допустимым. Для этого подставляем координаты вектора в ограничения:

Так как второе ограничение выполняется как строгое неравенство, то в силу УДН для оптимальности вектора необходимо выполнение равенства.

Построим двойственную задачу.

Поскольку , то из третьего и четвертого ограничений получаем . Но по УДН из условияследует, что должно выполняться равенство в первом ограничении двойственной задачи:

Подставляя значения получимСледовательно, УДН не выполняются и векторне является оптимальным в исходной задаче.

5. Метод Гомори

5.1. Постановка задачи цлп

Задача целочисленного программирования (ЦЛП) формулируется так же, как и задача ЛП, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение должны быть целыми неотрицательными числами:

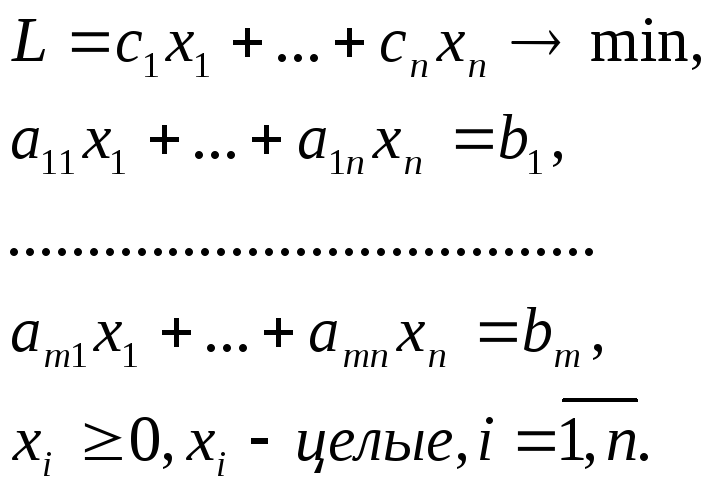(22)

Симплекс – метод не гарантирует целочисленности решения задачи (22), поэтому для отыскания оптимального целочисленного решения задачи ЦЛП требуются специальные методы. Один из таких методов, приводящий к целочисленному решению за конечное число шагов, предложен американским математиков Р. Гомори [1,2]. Идея метода следующая.

С помощью симплекс – метода решается задача ЛП без условия целочисленности. Если оптимальное решение получается нецелочисленным, то вводится дополнительное ограничение, которое, уменьшая многогранник допустимых решений (отсекая некоторую его часть), не исключает из него целочисленных точек. Если оптимальное решение задачи ЛП с дополнительным ограничением целочисленное, то вычисления заканчивают; если же оптимальное решение содержит хотя бы одну дробную компоненту, добавляют новое дополнительное ограничение.

Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо не будет найдено целочисленное оптимальное решение, либо показано, что задача не имеет целочисленных решений.