Понятие множества и операции над множествами. Типология множеств. Представление множеств на языке семантических сетей.
Множество – одно из фундаментальных математических понятий, относящихся к числу неопределённых. Его можно только пояснить:
*Множество – это некоторое количество объектов, объединяемых в одно целое. Указанные объекты считаются элементами формируемого из них множества
*Множество – это многое, мыслимое нами как единое (Кантор, основатель теории множеств)
*Множество – условная надстройка над некоторой группой объектов любой природы, объединяющая эту группу объектов в некоторое мысленное (абстрактное) целое.
Множество есть нечто субъективно привносимое, в природе множеств нет. Ил любого набора объектов можно составить множество, элементами которого будут эти и только эти объекты. Элементами одних множеств также могут быть другие множества. Это позволяет строить сложную иерархическую систему множеств.
Знак множества – некий объект, главным свойством которого является обозначать, быть представителем некоторого конкретного множества. Облик и внутреннее устройство может быть самым различным.
Типология:
1. по нормализованности:
Нормализованное множество (множество, каждый элемент которого является знаком множества)
Ненормализованное множество – множество, среди элементов которого имеется хотя бы один элемент не являющийся знаком множества.
Почти нормализованное множество
Мощность множества – суммарное количество вхождение в это множество всех его элементов
по мощности и ориентированности:
одномощное множество – 1-элементное множества с однократным вхождением элемента
предметное множество (предмет)
пара – мощность множества равна 2 (1-элементные с 2кратным вхождением, или двухэлементные с однократным вхождением)
простая ориентированная пара – ориентированное множество, состоящее из 2х элементов каждый из которых входит однократно в состав этого множества, один из них считается первым компонентом, а второй вторым, либо из оного элемента 2кратно входящего в состав множества, одно вхождение его считается первым вхождением, а второе вторым. Знаки таких пар – дуги.
пара принадлежности
пара непринадлежности
пара нечёткой принадлежности
неориентированная пара
пара синонимии – связывают семантически эквивалентные знаки
пара несинонимии – представляют неориентированные пары не являющиеся синонимами
пара нечёткой синонимии – достоверно неизвестно, являются они синонимами или нет.
тройка
Ещё бывают пустые множества
по семантике
пара принадлежности – множество частного вида, состоящие либо из двух элементов, один из которых считается знаком множества, а второй – одним из элементов указанного множества, либо из двух вхождений одного и того же элемента, который трактуется как знак некоторого множества, включающего в качестве одного из своих элементов знак самого себя (петля принадлежности)
узловое множество – множество, не являющееся парой принадлежности.
предметное множество (предмет) – множество состоящее из одного и однократно входящего в его состав элемента, которым является указанный предмет, который не является ни множеством, ни знаком множества..
узловое непредметное множество
простая ориентированная узловая пара
пара непринадлежности
пара нечёткой принадлежности
неориентированная пара
пара синонимии
пара несинонимии
пара нечёткой синонимии
семейство дуг принадлежности – множество, каждым элементом является дуга принадлежности
семейство узловых множеств – множество, каждым элементом которого является знак некоторого множества
семейство предметных множеств -//- знак предметного множества
семейство узловых непредметных множеств -//- знак узлового непредметного множества
система множеств – множество, состоящее из некоторого количества узловых множеств или их знаков, а также пар принадлежности, которые связывают между собой указанные выше узловые множества и/или их знаки.
|
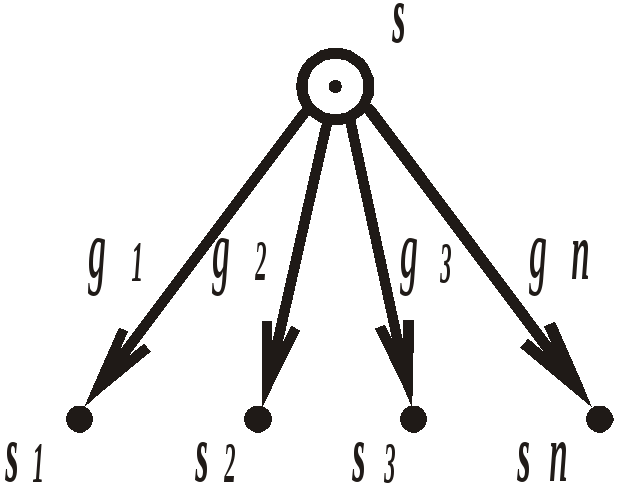
SCBg-текст 3.1.1. Вариант 1g изображения узлового непредметного множества (с явным изображением дуг, выходящих из узла s ) |
|
|
|
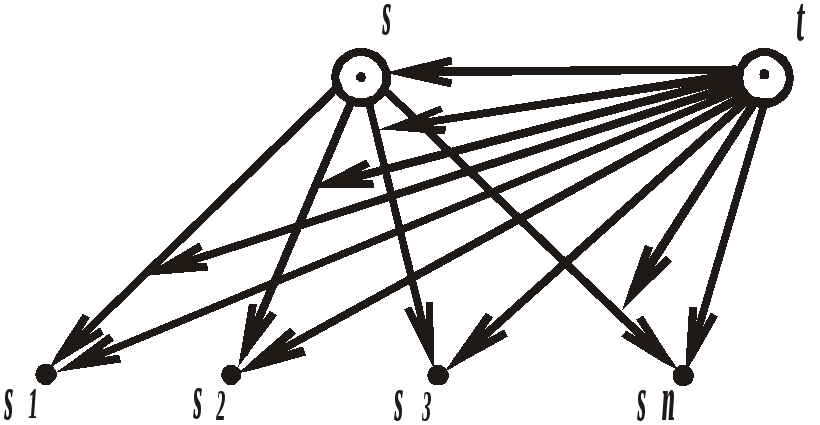
SCBg-текст 3.1.3. Вариант 1g изображения системы множеств (с явным изображением дуг, выходящих из узла t ) |
|
|
2. Сочетания, размещения, перестановки, булеаны.
Отношение предельного вида – семейство знаков всевозможных множеств, удовлетворяющих какому-то конкретному свойству (требованию):
множество всевозможных классических кортежей, каждый из которых использует заданный набор атрибутов
множество всевозможных классических кортежей
множество всевозможных кортежей.
Кроме конкретных отношений предельного вида существует ряд классов отношений предельного вида:
декартовы произведения (прямые произведения)
булеаны
отношения, каждое из которых является множеством всевозможных перестановок из заданного набора элементов
отношения, каждое из которых является множеством всевозможных сочетаний заданной мощности из заданного набора элементов
шкалы множеств
отношения, каждое из которых является универсумом, построенным на заданном множестве.
Встречные кортеж – кортежи, состоящие из одинаковых элементов, по крайней мере один из который входит в разные (встречные) кортежи под разными атрибутами.
1. Отношение р будем называть множеством перестановок в том и только в том случае, если оно обладает следующими свойствами:
является классическим отношением
не имеет связок с кратными вхождениями элементов
все его связки являются встречными друг другу (то есть любые 2 связки отношения р являются встречными кортежами)
каждый встречный кортеж любого кортежа входящего в отношение р также входит в состав отношения р
2. Рассмотрим семейство неориентированных отношений, не имеющих кратных связок и не имеющих связок с кратными вхождениями элементов. Для такого семейства отношений можно построить минимальное «отношение предельного вида», являющееся подмножеством для всех отношений, удовлетворяющих указанным выше свойствам. Для этого достаточно построить множество, являющееся результатом объединения областей определения всех отношений, входящих в состав заданного семейства неориентированных отношений и для построенного множества построить семейство всевозможных его подмножеств. Указанное отношение предельного вида будем называть булеаном.
3. Рассмотрим семейство m-арных неориентированных отношений, не имеющих кратных связок и не имеющих связок с кратными вхождениями элементов. Для такого семейства отношений можно построить минимальное отношение предельного вида, то есть минимальное отношение, являющееся надмножеством для всех отношений, удовлетворяющих указанным выше свойствам. Для этого необходимо построить множеством, являющееся объединением областей определения всех отношений, входящих в состав заданного семейства неориентированных отношений, и для построенного множества построить семейство всевозможных его подмножеств, имеющих мощность, равную m. Указанное отношение предельного вида будем называть множеством сочетаний из заданного множества по m элементов.
3. Понятие атрибута, кортежа и схемы отношения. Представление атрибутов, кортежей и схем отношений на языке семантических сетей.
Кортеж – множество, у которого каждому вхождению каждого его элемента явно или неявно (по умолчанию) ставится в соответствие некоторый атрибут, указывающий роль этого вхождения элемента в рамках рассматриваемого кортежа. Формально атрибут вхождений элементов в кортежи- это множество знаков пар принадлежности, связывающих знаки кортежей с такими же вхождениями их элементов, которые в рамках указанных кортежей выполняют некоторую одинаковую роль. Кортеж – это множество, для которого существенным является не только набор вхождений элементов в это множество, но и дополнительное явное указание роли (атрибута) в рамках этого множества хотя бы одного вхождения какого-либо его элемента. Кортежи так же называют ролевыми структурами, упорядоченными наборами, упорядоченными множествами, ориентированными множествами, векторами. В частном случае атрибуты могут быть числовые. В кортеже с числовыми атрибутами все вхождения его элементов нумеруются от 1 до некоторого n. Числовой атрибут – это условный порядковый номер вхождения элемента в кортеж. Количество всех вхождений в состав кортежа всех его элементов будем называть мощностью кортежа.
Один и тот же объект может быть элементом различных кортежей. При этом в рамках различных кортежей этот объект может иметь разные атрибуты.
Множество, не являющееся кортежем – неориентированное множество.
Принципиальное свойство атрибута – указание того, к какому атрибуту относится та или иная пара принадлежности, выходящая из знака кортежа, задаёт семантику соответствующего кортежа.
Схема отношения r – множество знаков всех тех и только тех атрибутов, которые используются в кортежах отношения r.
Если в кортежах отношения используется атрибут, задаваемый по умолчанию, то в схеме этого отношения знак этого атрибута должен быть явно указан, а также явно отнесён к числу элементов специального множества, обозначаемого scb-узлом с идентификатором «атрибут по умолчанию»
В состав отношения могут входить не только знаки кортежей, но и знаки неориентированных множеств
Атрибут, знак которого входит в схему отношения r может использоваться не в каждом кортеже, который входит в состав отношения r.
|
|
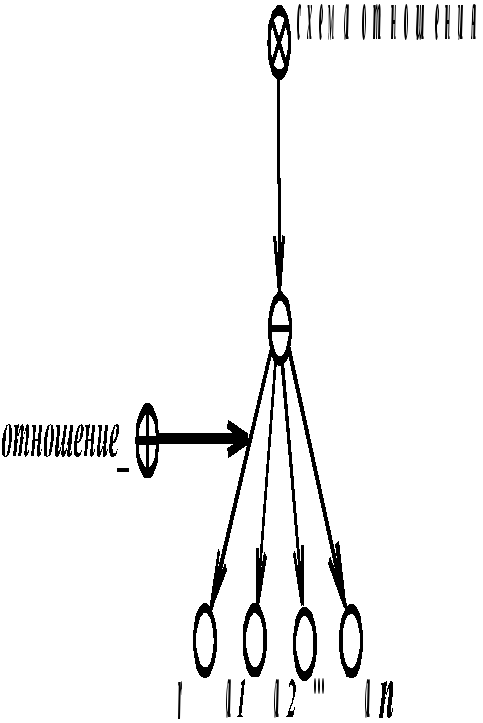
SCBg-текст 3.3.13.1. Общий вид отношения ” схема отношения” Здесь r – знак некоторого отношения a1, a2, …, an – знаки всех тех и только тех атрибутов, которые используются в связках отношения r. |
|
| ||
|---|---|---|---|---|---|
|
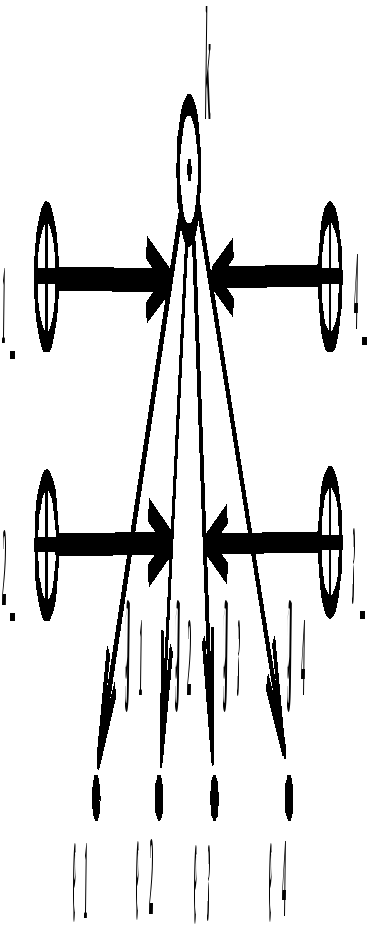
SCBg-текст 3.2.2.1. Вариант 1g изображения 4-мощного кортежа Здесь:
|
|
| |||
Понятие отношения. Операции над отношениями. Представление отношений на языке семантических сетей.
Отношение представляет собой некоторое семейство однотипных в каком-то смысле множеств. В состав отношений могут входить как неупорядоченные множества, так и кортежи.
Нормализованное отношение – множество знаков нормализованных множеств, каковыми в частности могут быть кортежи нормализованное отношение можно трактовать как иерархическую конструкцию, состоящую из следующих уровней:
знак самого отношения
знаки нормализованных множеств, являющихся элементами отношения (могут быть как неупорядоченными множествами, так и кортежами)
знаки атрибутов, используемых для указания роли элементов в кортежах, знаки которых являются элементами отношения
знаки множеств, являющиеся элементами множеств, знаки которых являются элементами отношения. (могут быть либо нормализованными, либо ненормализованными, но одномощными)
Входящие в состав отношения кортежи и неориентированные множества – связки этого отношения. Связка – множество, знак которого принадлежит к какому-либо нормализованному отношению.
Классическое отношение – множество знаков нормализованных классических кортежей, имеющих одинаковую мощность и использующих одинаковые атрибуты.
Переход от классической трактовки к широкой – допущение использования в качестве связок не только классических, но и неклассических кортежей, а также неориентированных кортежей и неориентированных множеств, допущение неодинаковой мощности связок и допущения использования разных атрибутов в разных кортежах.
Область определения отношения – множество всех тех и только тех объектов, которые являются элементами связок отношения.
Домен (унарная проекция) отношения r по атрибуту ai – это множество всех тех и только тех объектов, которые являются такими элементами связок отношения r, вхождения которых в эти связки имеют атрибут ai
|
SCBg-текст 3.3.3.1. Вариант 1 изображения отношения сложения Это классическое тернарное коммутативное отношение с атрибутами “слагаемое1_”, “слагаемое2_”, сумма_”. |
|
|
