
- •1. Словарные функции.
- •Словарные функции.
- •2. Вычислимые функции. Мт.
- •3. Словарное предствление мт.
- •4. Массовые алгоритмические проблемы. Разрешимые и перечислимые множества.
- •5. Теорема Поста.
- •6. Проблема остановки. Теорема Тьюринга.
- •7. Проблема пустой ленты. Проблема зацикливания.
- •Проблема зацикливания.
- •8. Понятие массовой и индивидуальной задачи.
- •9. Понятие полиномиального алгоритма и труднорешаемой задачи
- •10. Понятие схемы кодирования.
- •11. Задачи распознавания. Переход от оптимизационной задачи к задаче распознавания
- •Np – полные задачи.
- •Задачи разновидности языка и кодирование.
- •Примеры. Массовая задача и изоморфизм подграфу.
- •12. Язык. Связь между задачами распознавания и языками. Задачи разновидности языка и кодирование.
- •Примеры. Массовая задача и изоморфизм подграфу.
- •13. Детерминированные мт и класс p.
- •14. Недетерминированное вычисление и класс np.
- •15. Взаимоотношения между класами p и np.
- •16. Полиномиальная сводимость.
- •17. Np-полные задачи.
- •18. Теорема Кука. 6 основных np-полных задач.
- •Доказательство результатов об np-полноте.
- •Шесть основных np-полных задач.
- •19. Методы док-ва np-полноты. Метод сужения. Некоторые методы доказательства np-полноты.
- •Сужение задачи.
- •20. Методы доказательства np-полноты. Метод локальной замены Некоторые методы доказательства np-полноты.
- •Локальная замена.
- •21. Методы доказательства np-полноты. Метод построения компонент. Некоторые методы доказательства np-полноты.
- •Метод построения компонент.
- •22. Анализ подзадач np-полной задачи. Применение теории np-полноты для анализа задач.
- •Анализ подзадач.
- •23. Сильная np-полнота.
- •24. Псевдополиномиальные алгоритмы.
- •25. Именная форма. Высказывания. Операции над высказываниями.
- •26. Основные логические законы. Логические тождества.
- •27. Правила обращения с кванторами.
- •28. Техника доказательств.
- •29. Операции над множествами и одноместными предикатами.
- •30. Булевы функции.
29. Операции над множествами и одноместными предикатами.
Одноместным предикатом на множестве А называется функция отображающее множество А {0,1}. Пусть х некоторое подмножество А, определяем х: А {0,1}
х(а)=
х называется характеристической функцией подмножества х.
Операции над множествами и одноместными предикатами:
Пусть f,g отображают А{0,1}. Определим функцию f через g: А{0,1}.
(fvg)(a)=f(a)Vg(a). Аналогично fg и g
Две постоянные функции: 0: А{0,1}
1: А{0,1}
О(а)=0, 1(а)=1
Теорема: Пусть X,Y , тогда:
х V Y = x
 y
yх Y = x
 y
y x = x
0=0, 1=A
доказательство: пусть аА
(хVY)(a)=
х(a)V
Y(a)=
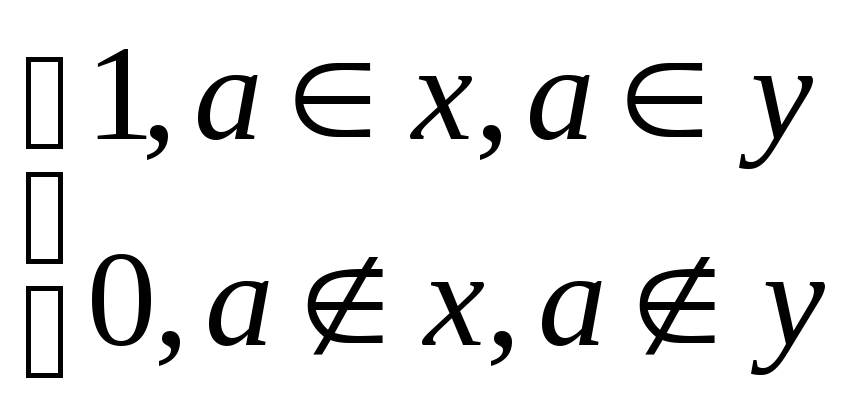
То есть первое тождество доказано, а второе аналогично. Теперь рассмотрим третье тождество:
(х)(a)=
(х)(a)=
x
(a)=
Четвёртое аналогично.
Следствие:
Пусть имеется логическое тождество в
которое входят только операции ,V,.
Тогда если вместо переменных подставить
имена подмножеств множества А и заменить
логические операции операциями над
множеством:
![]() ,
,![]() ,
,![]() , а константы 0,1 на пустое множество и
множество А, то получится верное тождество
для множеств.
, а константы 0,1 на пустое множество и
множество А, то получится верное тождество
для множеств.
30. Булевы функции.
Определение:
БФ от n
переменных - это отображение
![]()
Теорема: каждую БФ можно выразить через операцию V,, .
Доказательство: Пусть f:{0,1}n {0,1} – БФ от n переменных
Если
 (x1,x2,…,xn){0,1}n
f(x1…xn)=0,то
f(x1…xn)=x1
(x1)
(x1,x2,…,xn){0,1}n
f(x1…xn)=0,то
f(x1…xn)=x1
(x1)Пусть функция f тождественно
Рассмотрим
,x{0,1}.
Обозначим x
=
![]()
Для любого набора (1,2,…,n)для которого функция f принимает значение 1 мы заменим выражение вида:
X11x22…xnn
Дизъюнкция всех этих выражений даёт Булевую функцию f
Докажем это:S={(1…n) {0,1}n|f(1…n)=1 }
Тогда g(x1…xn)= V(x11x22…xnn)
(1…n)S
g(x1…xn)=f(x1…xn)
Определим при каких значениях x1…xn функции g=1когда (1…n)S,такой что X11x22…xnn=1
X11x22…xnn=1 i xi=i
Т.е. g(x1…xn)=1 для тех и только тех наборах который входят в множества S.
С другой стороны f(x1…xn)=1 для тех и только для тех, которые входят в множество S
Т.е. функции f и g принимают значение 1 и 0на одних и тех же наборах f=g
Следствие:каждую БФ можно выразить используя только 2 операции : или
Замечание:представленная
в теореме функция g
называется совершенная дизъюнктивная
нормальная форма исходя их подмножества
![]() =x
строится совершенная конъюнктивная
нормальная форма:
=x
строится совершенная конъюнктивная
нормальная форма:
(X11x22…xnn)
(1…n):
f(1…n)=0
Докажем: возьмём отрицание
(X11x22…xnn) = ((X11x22…xnn)=
(1…n): (1…n):
f(1…n)=1 f(1…n)=1
= ((X11)(x22)…(xnn))= (X11 x22 … xnn)
f(x1…xn) = ( f(x1…xn))
Пусть ρ(x1…xn)= f(x1…xn),
тогда
ρ(x1…xn)=

ρ(x1…xn)= (X11x22…xnn)
(1…n):
f(1…n)=0
f=-(ρ(x1…xn))= ((X11x22…xnn))= (X11 x22 … xnn)
(1…n):
f(1…n)=0
