ЦСАУ (ЦСАУЛР-1Вар-12)

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Кафедра компьютерных систем в управлении и проектировании (КСУП)

Лабораторная работа № 1

по дисциплине «Цифровые системы автоматического управления »

(Учебное пособие «Цифровые системы автоматического управления»,

автор А.Г. Карпов, 2004 г. )

Выполнил:

студент ТМЦДО

гр.: з-517-а

специальности 220201

Пономарев Сергей Сергеевич

29 сентября 2008 г.

г. Омск

2008 г

Лабораторная работа № 1

Цель лабораторной работы – освоить на практике методы получения и анализа уравнений состояния цифровой системы автоматического управления.

Исходные данные:

Задана импульсная передаточная функция замкнутой системы

№ варианта	W(z)
12

Необходимо:

1. Построить диаграммы состояния с помощью трех методов декомпозиции:

а) непосредственной,

б) последовательной,

в) параллельной.

2. Составить уравнения состояния и уравнения выхода на основе диаграмм состояния

Для каждого из методов п.1 результат представить в виде квадратной матрицы А, вектор-столбца В и вектор-строки С.

3. Решить уравнения состояния и уравнения выхода. Для этого:

а) вычислить переходную матрицу Ф(k),

б) записать решение уравнения в форме

Переходная матрица Ф(k) вычисляется для уравнений состояния, полученных

• непосредственной декомпозицией – с помощью метода z-преобразования;

• последовательной декомпозицией – с применением теоремы Кэли-Гамильтона;

• параллельной декомпозицией – как диагональная матрица.

Подстановка решения x(k) дает решение для выходного сигнала системы

Решение необходимо записать для k=3 для заданных r(k) и нулевых начальных условий (y(0) = y(1) = 0). Для записи решения требуется пересчитать начальные условия для y(k) в начальные условия для x(k).

Решение:

1. Построение диаграмм состояния

Непосредственная декомпозиция

При непосредственной декомпозиции удобнее передаточную функцию представить в виде отношения полиномов по степеням z ^–1:

где Y(z) и R(z) – z-изображения выходного и входного сигнала соответственно.

Преобразуем передаточную функцию к виду отношения полиномов по степеням z^–1, разделив числитель и знаменатель на z²:

Умножив числитель и знаменатель передаточной функции на вспомогательную переменную X(z), получим:

По последним уравнениям рисуем диаграмму состояния системы.

1

R(z) 1 X(z) z^1 z^1 0,4 Y(z)

r(kT) x₂((k+1)T) –0,3 x₂(kT)=x₁((k+1)T) x₁(kT)

0,54

Переменные состояния вводим после каждого ребра с весом z^–1. По полученной диаграмме записываем уравнения состояния и уравнение выхода, не учитывая ребер с весом z^–1:

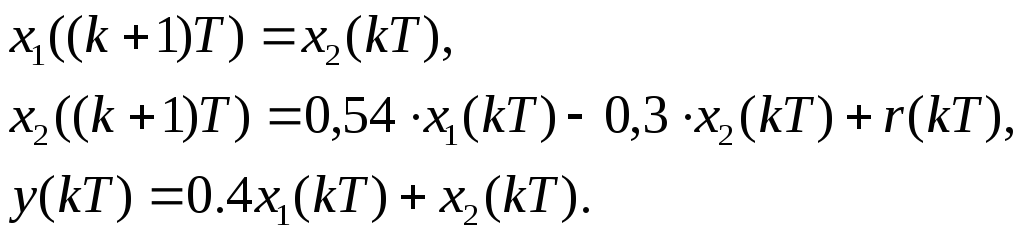
Из уравнений состояния и уравнения выхода видно, что соответствующие матрицы равны:

Непосредственная декомпозиция всегда приводит к уравнениям состояния системы в стандартной форме, или, как ее еще называют, к канонической форме фазовой переменной.

Параллельная декомпозиция

Параллельная декомпозиция предполагает разложение импульсной передаточной функции на простые дроби.

Представим передаточную функцию в виде суммы простых дробей, используя обычные правила разложения на простые дроби:

Диаграмма состояния, соответствующая этой передаточной функции, имеет следующий вид.

z^1 x₁(kT)

x₁((k+1)T)

0,6

r(kT) 0,666 1

y(kT)

0,333 z^1 1

x₂((k+1)T) x₂(kT)

–0,9

Вводя переменные состояния после каждого ребра с весом z^–1, составим уравнения состояния и уравнение выхода:

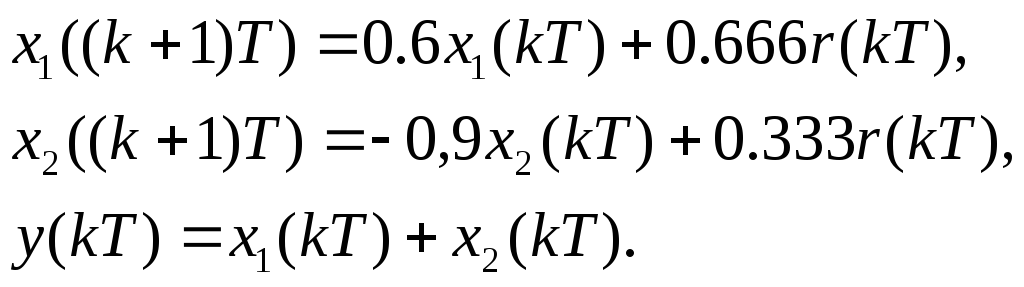
Соответствующие матрицы в привычных обозначениях будут равны:

При параллельной декомпозиции каждая компонента вектора состояния x_k зависит только от самой себя в предшествующий момент времени, и матрица А имеет диагональный вид со своими характеристическими числами на главной диагонали. Таким образом, уравнения состояния представляются в нормальной (канонической) форме.

Последовательная декомпозиция

Последовательную декомпозицию лучше всего использовать для действительных полюсов и нулей импульсной передаточной функции. В этом случае представим W(z) в виде:

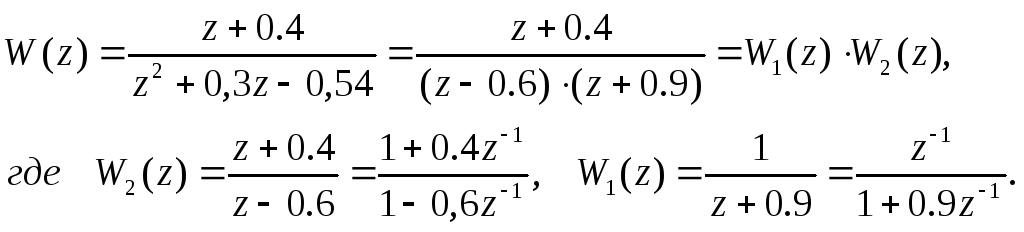
Составляем диаграмму состояния в виде последовательно соединенных цепочек.

1

r(kT) x₂((k+1)T) z^1 x₂(kT) x₁((k+1)T) z^1 x₁(kT) y(kT)

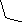
1 0,4 1

0,6 -0,9

По диаграмме состояния записываем уравнения состояния и уравнение выхода:

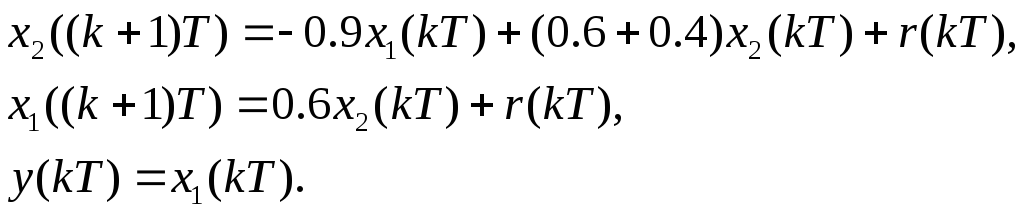
Окончательно матрицы в уравнениях системы будут иметь вид:

3. Решение уравнений состояния и уравнений выхода.

3.1. Вычисление переходной матрицы Ф(k)

3.1.1. Для уравнений состояния, полученных непосредственной декомпозицией переходная матрица вычисляется с помощью метода z-преобразования.

Найдем переходную матрицу для матрицы

методом z-преобразования. Для этого воспользуемся формулой .

Вначале запишем матрицу (zE–A):

.

Далее найдем обратную матрицу:

.

Умножая последнее выражение на z и проводя небольшие преобразования, получаем:

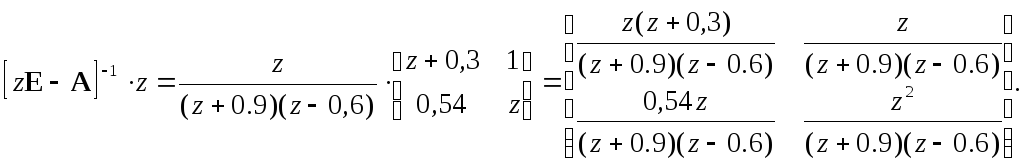
Осталось взять обратное z-преобразование от каждого элемента последней матрицы, предварительно представив эти элементы в виде суммы простых дробей. Имеем:

Таким образом, получили следующую переходную матрицу

Перейдем к решению уравнений

при

Считаем, что входное воздействие – единичная ступенька

Решение уравнения записывают в форме

Подстановка решения x(k) дает решение для выходного сигнала системы

Запишем решение для k=3 заданных r(k) и нулевых начальных условий (y(0) = y(1) = 0). Для записи решения требуется пересчитать начальные условия для y(k) в начальные условия для x(k).

Имеем

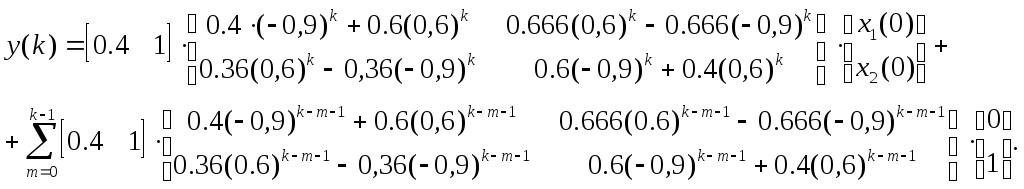
Подставляя в последнюю формулу k=0, получаем:

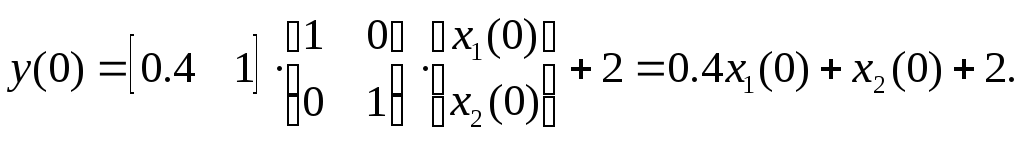
Полагая k=1, имеем:

Учитывая начальные условия для выхода y(k), получим начальные условия для вектора состояния x(k): Для того чтобы получить значения выхода в произвольный момент времени, необходимо подставить конкретное значение k и найденное значение x(0) в выражение для выходного сигнала. Для k=2, 3 получим

3.1.2. Для уравнений состояния, полученных последовательной декомпозицией переходная матрица вычисляется с применением теоремы Кэли-Гамильтона.

Найдем переходную матрицу для матрицы

методом Кэли-Гамильтона.

Поскольку матрица А имеет размерность (22), переходную матрицу можно представить как матричный полином первого порядка , где коэффициенты определяются из системы уравнений

где ₁, ₂ – собственные числа матрицы А.

Определяем собственные значения матрицы А, для чего составляем характеристическое уравнение:

.

Корни характеристического уравнения (собственные числа) равны ₁= –0,9; ₂= 0,6. Подставляя данные в систему уравнений, получим

Вычитая из первого уравнения второе, найдем ₁, а вычитая из первого уравнения удвоенное второе, определим ₀:

.

Осталось подставить найденные коэффициенты в выражение для переходной матрицы:

Перейдем к решению уравнений

при

Считаем, что входное воздействие – единичная ступенька

Решение уравнения записывают в форме

Подстановка решения x(k) дает решение для выходного сигнала системы

Запишем решение для k=3 заданных r(k) и нулевых начальных условий (y(0) = y(1) = 0). Для записи решения требуется пересчитать начальные условия для y(k) в начальные условия для x(k).

Имеем

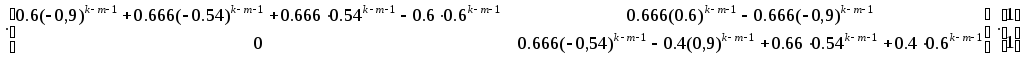
Подставляя в последнюю формулу k=0, получаем:

Полагая k=1, имеем:

Учитывая начальные условия для выхода y(k), получим начальные условия для вектора состояния x(k): Для того чтобы получить значения выхода в произвольный момент времени, необходимо подставить конкретное значение k и найденное значение x(0) в выражение для выходного сигнала. Для k=2, 3 получим

3.1.3. Для уравнений состояния, полученных параллельной декомпозицией переходная матрица вычисляется как диагональная матрица.

Составим модальную матрицу, предварительно определив собственные значения и собственные векторы матрицы

Составляем характеристическое уравнение:

.

Корни характеристического уравнения (собственные числа) равны

₁= 0,6, ₂= -0,9. Собственные векторы найдем как любой ненулевой столбец присоединенной матрицы

при ₁= 0,6, ₂= -0,9:

,

Таким образом, модальная матрица будет иметь вид:

.

Обратная к модальной матрица будет

.

Теперь запишем переходную матрицу

Перейдем к решению уравнений

при

Считаем, что входное воздействие – единичная ступенька

Решение уравнения записывают в форме

Подстановка решения x(k) дает решение для выходного сигнала системы

Запишем решение для k=3 заданных r(k) и нулевых начальных условий (y(0) = y(1) = 0). Для записи решения требуется пересчитать начальные условия для y(k) в начальные условия для x(k).

Имеем

Подставляя в последнюю формулу k=0, получаем:

Полагая k=1, имеем:

Учитывая начальные условия для выхода y(k), получим начальные условия для вектора состояния x(k): Для того чтобы получить значения выхода в произвольный момент времени, необходимо подставить конкретное значение k и найденное значение x(0) в выражение для выходного сигнала. Для k=2, 3 получим

Результаты при вычислениях всеми тремя методами практически совпадают (есть небольшие различия, что можно объяснить округлением), что подтверждает их правильность.