3.4. Логики умолчаний

Логики умолчаний, введенные и развитые Рейтером для формализации рассуждений, являющихся всего лишь выполнимыми, во многих отношениях аналогичны логикам, описанным в предыдущих главах. В частности, Рейтер интерпретирует умолчания точно также, как Мак-Дермотт и Дойл, т.е. утверждение «А есть обычно (как правило, типично) В» интерпретируется как «если xесть А и непротиворечиво предположить, чтоxесть В, тогдаxесть В». Однако, логики Рейтера отличаются от модальных подходов одним важным аспектом: вместо расширения логического языка и представления умолчаний в языке,умолчанияиспользуются какдополнительные правила вывода, индуцируя так называемыерасширенияклассических логических теорий. Умолчания определяют, каким образом логическая БЗ может быть расширена на множество предположений (убеждений), содержащее формулы, логически невыводимые в классическом смысле из БЗ.

При неполной информации мы вынуждены получать всего лишь правдоподобные предположительные заключения. Часто имеются утверждения, которые в большинстве случаев истинны, но допускают исключения. Логика первого порядка не является подходящей для выражения исключений, так как она требует явного упоминания всех исключений, что на практике невозможно выполнить

Если известно, например, что обычно студенты юны и Петров – студент, то выводимо, что Петров юн. Но не все студенты юны, имеются студенты, которым около или за 30 лет (предполагая, что юность длится лет до 23). Естественно сделать общее заключение, что Петров юн, если нет никакой другой дополнительной информации. Это и есть рассуждение с умолчанием.

Логики умолчаний позволяют формализовать такие рассуждения в виде правил вывода, называемых умолчаниями: .

Интуитивный смысл этого правила: если мы убеждены в и еслине противоречит тому, в чем мы убеждены (не противоречит тому, что известно), то мы убеждаемся и в.

И таким образом, правило «студенты обычно юны» выразимо в виде: , т.е. еслиx– студент и если это не противоречит, чтоxюн, то выводимо «xюн». Общее правило с исключениями гласит, чтообычно(как правило, типично) студенты юны. Это правило умолчания позволяет обрабатывать исключения без их предварительной идентификации.

Система логики умолчаний представляется теорией с умолчаниями, состоящей из некоторого множества особо выделенных формул и правил вывода. В ней содержатся формулы логики предикатов, представляющие основную информацию о прикладной системе, обрабатываемую в соответствии с имеющимися аксиомами, а также имеются правила умолчаний, отражающие исключения.

Для такой системы существует несколько (ноль или больше) множеств выводимых предположений. Эти множества представляют различные картины мира, которые можно вообразить, исходя из теории с умолчаниями.

Опять обозначим через Lязык предикатов первого порядка.

Правило умолчания(сокращенно: умолчание)D– это выражение вида, где(x),₁(x), …,_m(x) и(x) - формулы языкаL, свободные переменные у которых выбраны средиx = (x₁ …, x_n);

(x) называетсяпредпосылкойумолчанияD;

_i(x) –обоснованиемумолчанияD(i = );

(x) –следствиемумолчанияD;

М – некий символ метаязыка (например, «непротиворечиво»).

Умолчание Dназываетсязамкнутымтогда и только тогда, когда(x),₁(x), …,_m(x) и(x) не содержат свободных переменных. При этом можно использовать более простые обозначения,₁, …,_mисоответственно.

Свободные переменные умолчания считаются -квантифицированными. Область действия этих кванторов простирается на все члены умолчания. Незамкнутое умолчание называетсяоткрытым. Оно представляет общую схему вывода. Его конкретизацией является замкнутое умолчание, полученное заменой всех свободных переменных открытого умолчания на константы языка(с соблюдением неявного закона об области действия свободных переменных умолчания).

Теория с умолчаниями– это пара (D, F), гдеD– множество умолчаний,F– множество замкнутых формул изL. Она называетсязамкнутойтогда и только тогда, когда все умолчания изDзамкнуты.

Теория с умолчаниями = (D, F) подразумевает некоторое (нулевое или большее) число множеств предположений, которые выводимы с использованием множества формулF, и удовлетворяют свойству выполнимости. Эти множества предположений называютсярасширениямиданной теории с умолчаниями.

Расширения теории с умолчаниями явно определены здесь лишь для замкнутых теорий. Открытую теорию можно преобразовать эффективным образом в замкнутую, заменяя каждое открытое умолчание множеством всех его конкретизаций, получаемых посредством применения открытых умолчаний к универсуму Эрбрана данной теории. Используя это преобразование, полученные для замкнутых теорий с умолчаниями результаты можно распространить на открытые теории (когда они конечны). Заметим, что теории, содержащие функциональные символы ненулевой арности, имеют бесконечную эрбранову область.

Прежде чем приступить к формализации, охарактеризуем интуитивно свойства, которыми должно обладать расширение замкнутой теории с умолчаниями. Расширение– это подмножество основных сведений системы, включающее все выводимое (по правилам классической логики и/или логики умолчаний).

Пусть – подмножество формул изL,Th_L() – множество замкнутых формул,общезначимовыводимых изпо классическим правилам вывода изL:Th_L() = {w | w  L,wзамкнута и├w}.

Пусть = (D, F) – замкнутая теория с умолчаниями,S– подмножество замкнутых формул вL. Обозначим через(S)наименьшее подмножествовL, удовлетворяющее следующим трем условиям:

1. F  (S),

2. Th_L((S)) = (S),

3. если   D,   (S) и ₁, …, _m  S, то   (S).

Множество формул Е Lявляетсярасширениемдлятогда и только тогда, когда(Е) = Е (т.е. Е – неподвижная точка оператора).

Первое условиегарантирует то, что известно о мире, содержится в каждом расширении.Второе условиеговорит, что убеждения должны быть дедуктивно замкнуты, итретьеподразумевает тот эффект, что имеет место столько умолчаний, сколько их возможно относительно самого расширения. Кроме того, условиеминимальностиделает невозможным иметь «нефундаментальные» убеждения, т.е. неозначенные убеждения.

Расширение Е можно охарактеризовать так. Строим последовательность формул E_i, полагаяE₀ = FиE_i+1 = Th_L(E_i)  { |   Dи  E_iи₁, …, _m  E} дляi = 0, 1, 2, … Множество Е есть расширение длятогда и только тогда, когда Е =.

Теория с умолчаниями иногда позволяет вывести несколько расширений из од­но­го множества посылок. Если предпосылка всегда истинна, то ее можно опустить.

Пример 3.7. (Мак-Дермотт, Дойл). Пусть= (D, F), гдеF = { }, т.е.иD = , , . Эта теория обладает расширением Е =Th_L({P, S}).

Пример 3.8. Пусть= (D, F), гдеD = иF = . Эта теория не имеет расширений.

Пример 3.9. (Мак-Дермотт, Дойл). Пусть= (D, F), гдеD = , иF = . У этой теории два расширения:E₁ = Th_L({A}) иE₂ = Th_L({B}).

Пример 3.10. (Рейтер). Пусть= (D, F), гдеD = , , иF = . Расширений два:E₁ = Th_L({A}) иE₂ = Th_L({A, x P(x)}).

Например, первым умолчанием из Dможно формализовать «большинство про­фес­со­ров университета имеет степень доктора»:.

Как показывает пример 3.8, некоторые теории с умолчаниями не обладают расширениями. Существование расширений гарантировано, если следствие и обоснование одного и того же умолчания совпадают. Такие теории называются нормальными. Они состоят из нормальных умолчаний:.

Кроме интересного свойства допускать хотя бы одно расширение нормальная теория с умолчаниями обладает свойством полумонотонности: если увеличить множество умолчаний, то полученная теория допускает расширение, включающее какое-то расширение исходной теории. Практически важное следствие этого свойства состоит в возможности построения такой теории доказательств, в которой использованные умолчания проявляются локальным образом.

Пусть DиD– два множества замкнутых и нормальных умолчаний, таких, чтоD  D. Пусть Е– расширение для замкнутой и нормальной теории= (D, F) и пусть также= (D, F). Тогдаимеет расширение Е такое, что ЕЕ. При добавлении нового умолчания к теории, если имеет место полумонотонность, все, что было выведено в старой теории, останется выводимым в теории с новым умолчанием. Отсюда нет необходимости проверять предыдущие выводы при применении нового умолчания.

Можно ли построить теорию доказательств для логик умолчаний? В частности, для замкнутых нормальных теорий? Точнее, даны замкнутая нормальная теория и замкнутая формулаfизL. Существует ли метод проверки наличия длярасширения Е, содержащегоf?

Для получения ответа Рейтер определил доказательство в теории с умолчаниямиследующим образом. Пусть= (D, F) – замкнутая нормальная теория иf– замкнутая формула изL. Конечная последовательностьD₀, D₁, …, D_kконечных подмножеств изDесть доказательство дляfвтогда и только тогда, когда

1. F{KC(D₀)} ├f,

2. F{KC(D_i)} ├KT(D_i-1) дляi= ,

3. D_k = ,

4. F{KC(D_i) | 0ik} выполнимо,

где KC(D_i) – конъюнкция следствий иKT(D_i) – конъюнкция предпосылок умолчаний изD_i.

Итак, доказательство есть последовательность подмножеств умолчаний. Его можно интерпретировать следующим образом. Первое подмножество (D_k) выбирается пустым. Последовательно строясяD_k-1, …, D₁, D₀. Множество основных аксиом с добавленной к нему конъюнкцией следствий из всех умолчанийD₀должно обеспечивать доказательствоfклассическим образом. Из построения подмножестваD_i‑1вытекает, что множествоF(с добавленной к нему конъюнкцией следствий изD_i) должно позволять доказывать классическим образом предпосылки изD_i‑1и, следовательно, гарантировать применимость умолчаний изD_i‑1. Глобальная применимость всех умолчаний устанавливается проверкой выполнимости объединенияFи конъюнкций следствий всех использованных умолчаний.

Заметим, что в определении не говорится, как строить подмножества D_iи не приводится разрешающей процедуры для используемого отношения доказательства (из классической теории предикатов первого порядка). Более того, оно предполагает проверку выполнимости некой формулы изL, тогда как множество замкнутых выполнимых формул изLне являетсярекурсивно перечислимым.

Метод Рейтерасочетается со свойством полноты. Пустьf– замкнутая формула изL. Нормальная теория(замкнутая и выполнимая) обладаетрасширениемЕ (содержащимf) тогда и только тогда, когдаfобладает доказательством в.

К сожалению, во всех общности проблема проверки существования расширения с данной замкнутой формулой не полуразрешима (т.е. неразрешима). Это не столь неожиданно. Тем не менее, в некоторых случаях она поддается практическому решению (особенно когда ограничиваются рамками высказываний).

Нормальные умолчания выглядят достаточно привлекательными при представлении многих форм рассуждений. Свойства формальных систем, составляющих нормальные теории, особенно выигрышны в силу следующих обстоятельств.

Следствие и обоснование нормального умолчания совпадают. Следовательно, нормальные умолчания неприменимы, когда ложность их следствий доказана. Эти умолчания не могут вводить невыполнимости, опровергать обоснования из других ранее примененных нормальных умолчаний и своих собственных. Итак, нормальные теории полумонотонны, всегда обладают хотя бы одним расширением и представляют довольно простую теорию доказательств.

Между тем, в ходе применения нормальных умолчаний могут возникнуть неприятные осложнения. В частности, взаимодействие различных нормальных правил может приводить к нежелательным заключениям.

Поэтому иногда необходимо блокировать транзитивностьмежду умолчаниями. Например, рассмотрим нормальную теорию= (D, F), гдеDсодержит два нормальных умолчания:

1. «обычно студент университета является взрослым», или в символьном виде: ;

2. «обычно на работу берут взрослых», или в символьном виде:

и где F– множество из одного элемента {Ст(Петров)}.

Правила из Dпозволяют по умолчанию вывести, что студента университета взяли на работу. Это нежелательный вывод. Осложнение предотвращается с помощью третьего нормального умолчания: «обычно студентов не берут на работу». Таким образом, получается нормальная теория= (D, F), гдеD– множество умолчаний:,,. Для данного студента множествоDможет дать два расширения теории(соответствующих различной занятости студента):Th_L({Ст(Петров), Вз(Петров),Р(Петров)}) иTh_L({Ст(Петров), Вз(Петров), Р(Петров)}).

Тем не менее, разумно потребовать блокирования транзитивности между двумя первыми правилами из D. Следовало бы также выделить априори расширение, соответствующее ситуации, когда студента не принимают на работу. Это можно осуществить модификацией второго правила, чтобы оно не могло быть применено в исключительном случае – «взрослый является студентом». Итак, для теории= (D, F), гдеDесть,,, получаем желаемое расширениеTh_L ({Ст(Петров), Вз(Петров),Р(Петров)}).

Третье умолчание Dполунормальное, т.е. имеет вид:.

Таким образом, полунормальное умолчание явно управляется дополнительным условием в обосновании. Теория с полунормальными умолчаниями не обязательно обладает расширением. Она теряет некоторые достоинства нормальных теорий, в частности, полумонотонность.

Системы сетевого и объектного представлений часто позволяют выразить наследованиесвойств с исключениями и встроить механизмы вывода, связанные с этими методами. Поведение таких систем редко бывает корректным и полностью охарактеризованным. Соответствующие методы довольно плохо освоены.

Если наследственные свойства между классами и подклассами можно легко (относительно) охарактеризовать в классической логике, то исследование исключений требует ухищрений. Логика умолчаний очерчивает естественные рамки для формализации систем представления знаний и рассуждений с исключениями.

Между тем прямое обращение к теории с умолчаниями (в частности, к нормальной) простым не является. Наследственная система обеспечивает передачу свойств по транзитивности. Когда к системе добавляются исключения, транзитивность свойств должна допускать возможность блокирования.

В литературе предложены различные формализмы систем представления с механизмами наследования свойств.

1. Можно использовать полунормальные умолчания, как это сделали Этерингтон и Рейтер. Исключения для наследования свойств явноперечислены в умолчаниях. Этерингтон определил подкласс полунормальных умолчаний (связанных отношением зависимости), для которых соответствующие полунормальные теории всегда обладают хотя бы одним расширением. Он предложил процедуру эффективного построения полунормальных теорий.

2. Можно использовать нормальные умолчания с неявным порядком, подчиненным иерархии моделируемой структуры, как было предложено в работах Турецкого. Можно не упоминать явно исключения в умолчаниях.

3. Можно использовать таксономические теории с умолчаниями (не являющиеся ни нормальными, ни полунормальными). Они обладают единственными расширениями. Подробнее об этом можно узнать из работ Фройдевакса.

В заключении приведем пример.

Пример 3.11. Нормальные умолчания:

d₁= – обычно студенты юны;

d₂= – как правила, юные люди одиноки;

d₃= – одинокие люди юны;

d₄= – обычно студенты, имеющие детей женаты или являются сожителями;

d₅= – сожители юны.

Формулы:

F₁ = x(Од(x)Жен(x));

F₂ = x(Од(x)Сож(x));

F₃ = x(Сож(x)Жен(x)).

Дадим несколько примеров запросов. Формула fявляется ответом на запрос к БЗ, представленной с помощьюD = {d₁, …, d₅} иF = {F₁, F₂, F₃}, если существует, по крайней мере, одно расширение Е для (D, F) такое, чтоf Е.

1. Если Мария – студентка, то каков ее семейный статус? Добавим к FформулуF₄= Ст(Мария). Тогда₁ = (D, F  F₄) имеет расширение Е₁. Е₁содержит: Ст(Мария), Юн(Мария), Од(Мария),Жен(Мария),Сож(Мария), т.е. Мария – студентка, юна и одинока.

2. Если Мария – студентка и замужем, то каков ее статус? К FдобавляемF₄= Ст(Мария) иF₅= Жен(Мария).₂ = (D, F  {F₄, F₅}) имеет расширение Е₂, содержащее: Ст(Мария), Юн(Мария), Жен(Мария),Сож(Мария),Од(Мария). Здесь имеет место немонотонность: добавлениеF₅приводит к расширению Е₂, в котором блокируется Од(Мария). Точнее имеем свойство полумонотонности нормальных умолчаний, которое ограничивает необходимость ревизии старых доказательств.

3. Если Мария юна, каков ее статус? Добавляем F₆= Юн(Мария). Для₃ = (D, F  F₆) имеем расширение Е₃, содержащее: Юн(Мария), Од(Мария),Жен(Мария),Сож(Мария), но неизвестно, студентка она или нет.

4. Мария – студентка и может быть имеет детей. Каков ее статус? Добавляем F₄= Ст(Мария) и два умолчания:d₆ = 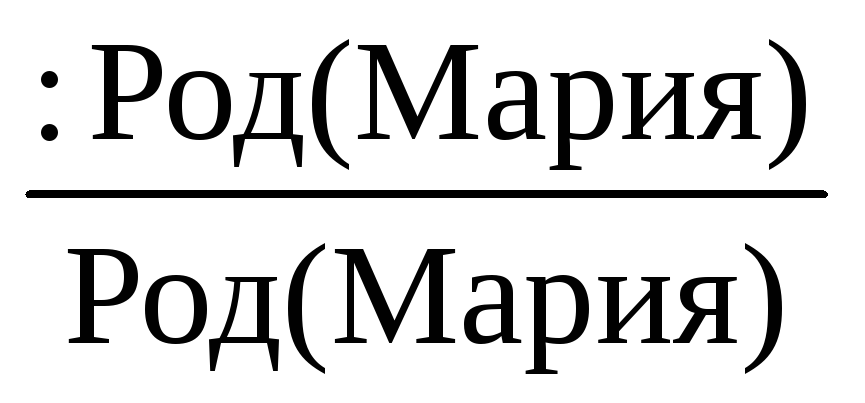иd₇ = . «Может быть» говорит о существовании двух типов расширений: она может иметь и может не иметь детей.₄ = {D  {d₆, d₇}, F  {F₄}) дает три расширения: Е₄,и. Каждое из них содержит: Ст(Мария), Юн(Мария). Кроме этого Е₄содержит: Род(Мария), Жен(Мария)Сож(Мария),Од(Мария);содержит: Род(Мария), Од(Мария),Жен(Мария),Сож(Мария);содержит:Род(Мария), Од(Мария),Жен(Мария),Сож(Мария). Мы не знаем точно, одинока ли Мария или нет, лишь знаем как о возможности ее быть одинокой (и), так и не быть (Е₄). Заметим, что эта ситуация отличается от предыдущей, в которой наше знание о студентке или не студентке Марии не было представлено. Здесь факты Ст(Мария) и Юн(Мария)необходимы, так как они присутствуют во всех трех расширениях, в то время как факт Од(Мария)возможен, т.е. он содержится не во всех расширениях.

5. Теперь модифицируем умолчания d₁d₅путем использования так называемых «свободных» умолчаний или нормальных умолчаний без предпосылок.

; ;

; ;

.

Тогда D = {}.

Умолчания d₁и имеют разный смысл:d₁выражает знание по обстоятельствам, а – постоянное знание. Умолчаниеd₁говорит о том, что когда речь идет о студенте, то предполагаем, что он априори юн. В случае с самого начала известно, что любой человек, если он – студент, априорно юн.

Имеем запрос: Мария не юна. Каков ее статус? К FдобавляемF₇=Юн(Мария). В случае с (D, F F₇) ничто не может быть выведено, кроме теорем, полученных изF. Единственное, что известно, это то, что Мария не юна. Во втором случае для₅ = (D, F  F₇) расширение Е₅содержит:Юн(Мария), Ст(Мария)Юн(Мария) и по контрапозицииСт(Мария). Аналогично,Од(Мария),Сож(Мария). Таким образом, Мария – не студентка, не одинока и не сожительница. Насколько правомерно применять контрапозицию?

6. Запрос: я не могу точно вспомнить, говорила ли Мария мне о том, что она – студентка или одинока? Добавляем F₈ = Ст(Мария)Од(Мария). В случае с (D, F  F₈) мы не имеем ничего касающегося Марии, в то время как при (D, F  F₈) расширение Е₆содержит: Ст(Мария)Юн(Мария), Од(Мария)Юн(Мария) и Ст(Мария)Од(Мария), и следовательно, Юн(Мария).

7. Если Мария – студентка и имеет детей, то каков ее статус? Добавляем F₄ = Ст(Мария) иF₉= Род(Мария).₇ = (D, F  {F₄  F₉}) допускает два расширения: Е₇и. Каждое из них содержит: Ст(Мария), Юн(Мария), Род(Мария) (используемd₁). Кроме того, Е₇содержит: Жен(Мария)Сож(Мария),Од(Мария) (полученное изd₄).содержит: Од(Мария),Жен(Мария),Сож(Мария). В данном случае такая двойственность статуса Марии здесь нежелательна. Поэтому предпочтительнее выбрать Е₇, поскольку информация, содержащаяся вd₄, более специфична, чем та, которая получена изd₁иd₂. Таким образом, в рассуждениях здравого смыслаd₄, касающееся более конкретного случая, ведет себя как исключение по отношению к общим правиламd₁иd₂. Отсюда ему можно дать приоритет. Но кто будет устанавливать эти предпочтения?

Выходом из создавшегося положения может быть введение полунормальных умолчаний типа: , что означает: «быть родителем есть исключение из факта, что юная персона должна быть априори одинокой». ПустьD = (D \ {d₂})  {}. Тогда= {D, F  {F₄, F₉}) имеет единственное расширение Е₇, соответствующее здравому смыслу. Заметим, что (D, F  F₄) допускает то же самое расширение Е₁, что и₁.

Главный недостаток такого представления умолчаний заключается в немодульностинаписания правил умолчания, т.е. добавление новых исключений может потребовать добавления новых формул для обоснования полунормальных умолчаний и, следовательно, модификации уже существующих правил.

Для сохранения модульности с каждым умолчанием d_iбудем связывать предикат утвержденияR_i(x), означающий, что умолчаниеd_iможет быть применено к х. Этих предикатов столько, сколько умолчаний. Для нашего примера имеем:

; ;

; ;

.

Для того чтобы дать предпочтение над, введем умолчание, которое блокирует. Умолчаниевыражает тот факт, что быть студентом и родителем не допускает вывода быть одиноким, если он был юным, т.е.. ИмеемD = {}. Умолчаниеиграет здесь управляющую роль, указывая, чтоявляется исключением для. В этом случае= {D, F  {F₄, F₉}) имеет единственное расширение, которое содержит Ст(Мария), Юн(Мария), Род(Мария), Жен(Мария)Сож(Мария),Од(Мария),R₂(Мария) с сохранениеммодульности.

Установим соотношение между логикой умолчаний и АЭЛ. На первый взгляд может показаться, что логика умолчаний менее выразительна, нежели АЭЛ, поскольку в ней нет возможности выводить умолчания из других формул, так как они не являются частью языка.

Тем не менее, как бы это не было удивительно, Конолиге показал, что АЭЛ и логика умолчаний эквивалентны. Эквивалентность здесь понимается в том смысле, что расширения теории с умолчаниями являются точно частью теории первого порядка, т.е. не содержащими оператор Lформулами некоторого класса расширений АЭЛ, называемых строго основанных расширений. Понятие строгой основанности гарантирует, что каждая замкнутая формулаfимеет вывод, который не зависит отLf.

Конолиге показал, что каждая автоэпистемическая теория может быть эквивалентно представлена в так называемой нормальной форме, в которой формулы имеют вид:L  L₁  …  L_n  , где, ₁, …, _n, не содержат оператораL(Lи/илиL_iмогут быть опущены). Такой вид формулы представляется как умолчаниеи обратно (операторLможет быть опущен). Если предпосылкаLопущена, то предполагается, что она всегда истинна.

Например, если в АЭЛ мы имели Ст(Петров) & LЮн(Петров)Юн(Перов), то в нормальном умолчании –.

Пусть А – множество замкнутых формул АЭЛ в нормальной форме и пусть Е – расширение для А. Пусть А– множество замкнутых формулL  L₁  …  L_n  для А такое, что ни одно из₁, …,_nне содержится в Е. Расширение Е строго основано на А тогда и только тогда, когда Е = {p | A  LA  LE ╞_SS p}, гдеLA– множество формул {Lp | p  A},LE– {Lp | p  E}, а ╞_SS обозначает логическое следствие с ограничением модальных индексов для устойчивых множеств (SS–stablesets).

Конолиге доказал следующую теорему.

Теорема 3.7.Для любого множества замкнутых формул А автоэпистемической логики имеется эффективно конструктивная теория с умолчаниями (D, F) и обратно, для каждой теории с умолчаниями (D, F) имеется эффективно конструктивное множество замкнутых формул А автоэпистемической логики такое, что Е является расширением теории с умолчаниями тогда и только тогда, когда оно является подмножеством теории первого порядка для расширений, строго основанных на А.

Этот результат удивителен. Мур понимал свою логику как формализацию автоэпистемических рассуждений, но не как формализацию рассуждений по умолчанию. Эквивалентность этих логик предполагает, что формы немонотонных рассуждений хоть и различны, но как автоэпистемические рассуждения, так и рассуждения по умолчанию не обязательно требуют различных формализаций.