МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПЕЧАТИ
Кафедра теоретической и прикладной механики
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовой работе на тему:
«МЕХАНИКА СПЛОШНОЙ СРЕДЫ»
Студент: Шишова Е.Ю.
Группа: ЗТ-34
Преподаватель: Яковлев Р.В.
Москва
Исследование скалярного поля
Скалярное поле – это область, в каждой точке которой задан скаляр.
Скаляр – (от лат.scalaris – ступенчатый) величина, значение которой выражается одним числом.
Для графического изображения скалярных полей используются поверхности уровней.
Поверхность уровня – это геометрическое место точек в пространстве, соответствующих одному и тому же значению скалярной величины (Ф(x,y,z)=const).
Если положение точек скалярного поля зависит только от двух координат, то скалярное поле графически будет изображено не поверхностью, а линией уровня, каждая точка которой также будет соответствовать одному и тому же значению скалярной величины.
Для построения поверхности или линии уровня, проходящей через заданную точку, необходимо подставить координаты этой точки в функцию, при помощи которой задано скалярное поле, и определить значение постоянной С. Далее необходимо приравнять саму функцию к найденной постоянной С.
Полученное уравнение будет описывать поверхность или линию уровня.
Через каждую точку проходит только одна линия уровня.
Скалярное поле характеризуется градиентом.
Градиент – вектор, определяющий направление и величину быстрейшего возрастания функции в окрестностях данной точки.
Значение градиента определяется выражением:
gradФ(x,y,z)=Ф=i(Ф/x)+j(Ф/y)+k(Ф/z) (1)
Значение абсолютной величины градиента определяется выражением:
|A|=x2+y2+z2 (2)
Свойства вектора градиента
Вектор градиента всегда перпендикулярен к касательной, проведенной к линии уровня в точке.
Для построения вектора градиента в данной точке необходимо подставить координаты этой точки в вычисленное по формуле (1) выражение и в выбранном масштабе отложить проекции вектора от данной точки и геометрически их сложить.
Задача 1.1.
Задана функция скалярного поля Ф(x,y,z)=x+z2и точки М1(1,1,1) и М2(2,2,2).
Требуется:
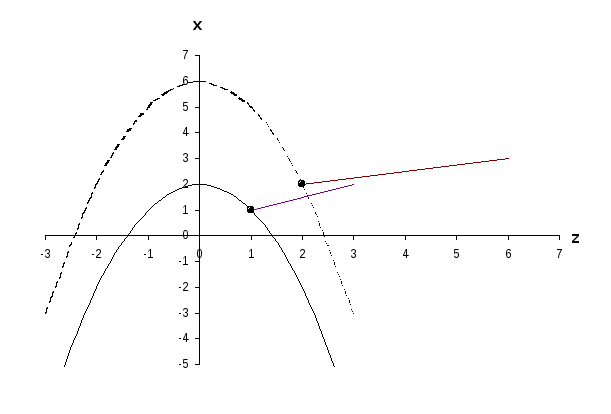
Построить две линии равного уровня заданной функции, проходящие через точки М1и М2.
В точках М1и М2построить векторы градиентов А1и А2.
Определить модуль скорости возрастания заданной функции в точках М1и М2.
Решение.
Подставим координаты точки М1в заданную функцию скалярного поля.
С=1+12=2
Приравняем найденную постоянную С к заданной функции.
x+z2=2 – уравнение линии уровня, проходящей через точку М1.
Подставим координаты точки М2в заданную функцию скалярного поля.
С=2+22=6
Приравняем найденную постоянную С к заданной функции.
x+z2=6 – уравнение линии уровня, проходящей через точку М2.
Найдем значение градиента.
gradФ=i((x+z2)/x)+j((x+z2)/y)+k((x+z2)/z)=i+2zk.
Тогда значение градиента в точке М1:
А1=i+2k;
в точке М2:
А2=i+4k.
Модуль скорости возрастания заданной функции в точке М1:
|A1|=1+22=5=2,24;
в точке М2:
|A2|=1+42=9=3.
Задача 1.2.
В переменных Лагранжа задано движение частицы сплошной среды
x=3t2
y=t2+3
и моменты времени t0=0c,t2=1c.
Требуется:
Определить и построить траекторию движения частицы.
Определить и построить на траектории движения в заданные моменты времени вектор скорости и ускорения частицы.
Решение.
Из второго уравнения системы выразим t2и подставим в первое.
t2=y-3 x=3(y-3)=3y-9.
x=3y-9 – уравнение траектории движения частицы.
Тогда в момент времени t0=0cкоординаты точки будут
х=3*02=0
y=02+3=3
В момент времени t2=1cкоординаты точки будут
x=3*12=3
y=12+3=4
Составим систему уравнений скоростей.
x=6t
y=2t
Тогда при t0
x=0,y=0;
При t2
x=6,y=2.
Составим систему уравнений ускорений.
x=6
y=2
Как видно, векторы ускорений в каждый момент времени постоянны.
