
Шпаргалка По Математической Логике (Дьячков А. М.)
.docx|
1.Алгебра высказываний, пропозициональные связи и формы, истинностные таблицы. Высказывания – повествовательное предложение, ктр можно приписать истинностное значение. Сокращенно истинностное значение «истина» обозначается цифрой 1 или буквой И, а «ложь» - цифрой 0 или буквой Л. Сами высказывания обозначаются латинскими буквами A, B, A1, A2… Для формализации и отражения высказываний на строгом математическом уровне вводятся операции над высказываниями. Определить каждую из этих операций – значит приписать истинностное значение результату операции в зависимости от истинностных значений ее аргументов.
Символы ¬, &, v, → и ≡ называются пропозициональными (или логическими) связками. Буквы, обозначающие высказывания, называются пропозициональными буквами. Осмысленные формулы, составленные из пропозициональных букв, пропозициональных связок, а так же скобок, указывающих порядок выполнения операций, называются пропозициональными формами. Обозначаются ПФ прописными латинскими буквами. Приоритет операций: ¬, &, v, → и ≡ |
2.Алгебра высказываний, тавтологии и противоречия. Все возможные комбинации истинностных значений пропозициональных букв в ПФ называются истинностными наборами. Если ПФ принимает значение 1 на любом истинностном наборе (тождественная «истина»), то эта ПФ называется тавтологией. Если же ПФ принимает значение 0 на любом истинностном наборе (тождественная «ложь»), то эта ПФ называется противоречием. Если ПФ не является противоречием, то она называется выполнимой. Из тавтологий получаются высказывания, истинные по форме, а из противоречий – ложные по форме (а не по содержанию). |
3. Алгебра высказываний, логическое следствие и логическая эквивалентность. Логическим следствием ПФ A называется такая ПФ B, что ПФ A→B является тавтологией. В этом случае говорят, что ПФ B логически следует из ,A или что A логически влечет B. Логически эквивалентными называются такие ПФ A и , что ПФ A≡B является тавтологией. Логическая эквивалентность ПФ в точности означает их совпадение как функций нескольких переменных, т.е. то, что на каждом истинностном наборе они принимают одинаковые значения. Логическая эквивалентность ПФ A и обозначается так: A ~B. Эквивалентности: Коммутативность A v B~ B v A A&B~B&A Дистрибутивность (AvB)&C~(A&C)v(B&C) (A&B)vC~(AvC)&(BvC) Ассоциативность (AvC)vC~Av(BvC) (A&B)&C~A&(B&C) Закон двойного отрицания ¬¬AA~A Законы де Моргана ¬(AvB)~ ¬A&¬B ¬(A&B)~ ¬Av¬B Законы поглощения AvA~A A&A~A Av¬A~1 A&¬A~0 Av1~1 Av0~A A&1~A A&0~0 А так же эквивалентности: A→ B~¬AvB A→ B~¬(A&¬B) A≡B ~(A→B)&(B→A) A≡B ~(A&B)v(¬A&¬B) |
|||||||||||||||||||||||||||||||||||
|
4. Алгебра высказываний: дизъюнктивная и конъюнктивная нормальные формы. Если A – пропозициональная буква
Элементарной конъюнкцией называется ПФ следующего вида:
При этом допустимо, чтобы n=1, в этом случае элементарная конъюнкция – это либо A1, либо ¬A1. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. При этом допускается, что может быть всего одно дизъюнктивное слагаемое. Дизъюнктивная
нормальная форма, зависящая от
пропозициональных букв A1,…,An,
называется совершенной (СДНФ), если
все дизъюнктивные слагаемые различны,
и каждое из них имеет вид
Элементарной дизъюнкцией называется ПФ следующего вида:
Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. При этом допускается, что может быть всего один конъюнктивный сомножитель. |
5.Алгебра высказываний: полные системы функций, базис. Система пропозициональных связок называется полной, если любая пропозициональная форма может быть записана с помощью только из этой системы. Система пропозициональных связок называется независимой, если никакая из связок этой системы не может быть выражена через другие связки той же системы. Полная независимая система связок называется базисом.
|
6.Понятие формальной аксиоматической теории. Задать ФАТ – значит определить следующие ее компоненты:
В ФАТ выводом или доказательством формулы A называется конечная цепочка формул, каждая из которых есть либо аксиома, либо непосредственное следствие каких либо из предыдущих формул по одному из правила вывода, причем последняя формула этой цепочки – это и есть формул A. Если для формулы A существует вывод, то говорят, что она является теоремой ФАТ, и пишут так: ├A. Пусть Г – некоторое множество формул ФАТ (гипотез или посылок). Мысленно добавим к аксиомам ФАТ все эти гипотезы. Если после этого формула A оказывается теоремой, то она является следствием множества гипотез Г (Г├A). |
|||||||||||||||||||||||||||||||||||
|
7.Исчислений высказываний как формальная аксиоматическая теория. В исчислении высказываний как ФАТ формулами будут все ПФ, а теоремами окажутся в точности тавтологии. Алфавит ИВ состоит из пропозициональных букв, пропозициональных связок ¬ и → и скобок. Формулы ИВ – это все ПФ, содержащие лишь связки ¬ и →. Аксиом в ИВ бесконечно много, но каждая из них получается из одной из следующих трех схем аксиом: A1: A→(B→A); A2:(A→(B→C))→((A→B)→(A→C)); A3:(¬B→¬A)→((¬B→A)→B) Подстановкой вместо A, B и C произвольных формул ИВ. Правило вывода в ИВ всего одно: формула B считается непосредственным следствием формул A и A→B. Это правило называется МР. Схемы теорем ИВ: Т1: A→A; Т2: (A→B)→((B→C)→(A→C)); Т3: (A→(B→C))→(B→(A→C)); Т4: ¬¬A→A; Т5: A→¬¬A; Т6: (¬B→¬A)→(A→B); Т7: (A→B)→(¬B→¬A); Т8: ¬A→(A→B); Т9: (A→B)→((¬A→B)→B); Т10: A→(¬B→¬(A→B)).
|
8. Формальная аксиоматическая теория, определение аксиомы, правила вывода. Аксиомы – те формулы, ктр считаются не нуждающимися в доказательстве. Правила вывода, определяющие, в каком случае мы считаем одну формулу непосредственным следствием других. В ФАТ выводом или доказательством формулы A называется конечная цепочка формул, каждая из которых есть либо аксиома, либо непосредственное следствие каких либо из предыдущих формул по одному из правила вывода, причем последняя формула этой цепочки – это и есть формул A. Если для формулы A существует вывод, то говорят, что она является теоремой ФАТ, и пишут так: ├A. Пусть Г – некоторое множество формул ФАТ (гипотез или посылок). Мысленно добавим к аксиомам ФАТ все эти гипотезы. Если после этого формула A оказывается теоремой, то она является следствием множества гипотез Г (Г├A). |
9. Формальная аксиоматическая теория, формализация понятий теоремы и ее доказательства. Если для формулы A существует вывод, то говорят, что она является теоремой ФАТ, и пишут так: ├A. -Пусть Г1 и Г2 – два множества формул, причем Г1 ≤ Г2 . Тогда если Г1├A , то Г2├A.. Это очевидно. - Пусть Г1 и Г2 – два множества формул, причем каждая из формул Г1 является следствием множества формул Г2. Тогда если Г1├A , то Г2├A. Это так же очевидно. -Следствие множества теорем само является теоремой. |
|||||||||||||||||||||||||||||||||||
|
10. Формальная аксиоматическая теория, теорема дедукции, правила силлогизма и перестановки посылок. Схемы теорем ИВ: Т1: A→A; Т2: (A→B)→((B→C)→(A→C)); Т3: (A→(B→C))→(B→(A→C)); Т4: ¬¬A→A; Т5: A→¬¬A; Т6: (¬B→¬A)→(A→B); Т7: (A→B)→(¬B→¬A); Т8: ¬A→(A→B); Т9: (A→B)→((¬A→B)→B); Т10: A→(¬B→¬(A→B)). Т2 называется правилом силлогизма, Т3 – правило перестановки посылок. Всякая формула, полученная по схемам Т1, Т2, Т3 – являются теоремами ИВ. Теорема дедукции. Пусть A и B – формулы ИВ. Тогда если A├B, то ├A→B. Утверждение обратное теореме дедукции, также верно. |
11. Исчисление высказываний: связь между теоремами исчисления и тавтологиями. Всякая теорема в ИВ является тавтологией, и наоборот, всякая тавтология является теоремой в ИВ. |
12. Логика предикатов: понятия терма и предиката, кванторы. Элементы предметной области – предметы. Для обозначения определенных предметов используются малые начальные буквы латинского алфавита. Такие предметы называются предметными постоянными. Малыми буквами конца латинского алфавита обозначаются неопределенные предметы множества, ктр называются предметными переменными. Функциональные буквы служат для того чтобы поставить некоторому набору предметов поставить в соответствие некий вполне определенный предмет по некоторому правилу. Функциональные буквы, примененные к предметам, порождают термы. Более точно: -предметные постоянные и предметные переменные суть термы; -если
Термы – предметы, записанные в специфической форме, когда возникает необходимость указать, что данный предмет может быть получен из других предметов по некоторому правилу. Предикаты – формулы вида:
Заданные
на n-ках
предметов, значениями которых являются
истинностные значения тех или иных
высказываний об этих предметах.
Заглавные буквы
|
|||||||||||||||||||||||||||||||||||
|
13. Логика предикатов: логическая общезначимость. |
14. Логика предикатов: эквивалентность формул логики предикатов. |
15. Логика предикатов: нормальные пренексные формулы. |
|||||||||||||||||||||||||||||||||||
|
16. Теория алгоритмов, нормальные алгорифмы Маркова. |
17. Теория алгоритмов, интуитивное понятие алгоритмов. |
18. Теория алгоритмов, нормальные алгорифмы Маркова как уточнение понятия алгоритма. |
|||||||||||||||||||||||||||||||||||
|
19. Теория алгоритмов. Машина Поста. |
20. Теория алгоритмов. Машина Тьюринга. |
21. Исчисление высказываний. Построение доказательства методом МР. |
|||||||||||||||||||||||||||||||||||
|
22. Исчисление высказываний. Построение доказательства методом резолюций. |
23. Исчисление высказываний. Построение доказательства методом Вонга. |
24. Исчисление доказательства. Перенос высказываний через знак выводимости. |





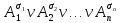
 – функциональная буква, и t1
,
…, tn
– термы, то
– функциональная буква, и t1
,
…, tn
– термы, то
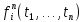 – тоже терм.
– тоже терм.
 называются предикатными буквами.
называются предикатными буквами.