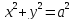Общее уравнение плоскости в пространстве
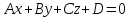 – общее уравнение плоскости в пространстве
– общее уравнение плоскости в пространстве
Нормальный вектор плоскости
Нормальным вектором плоскости назовем ненулевой вектор, ортогональный каждому вектору, лежащему в плоскости.
Уравнение плоскости, проходящей через
точку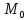 с заданным вектором нормали
с заданным вектором нормали
 – уравнение плоскости, проходящей через
точку M0 с заданным вектором нормали
– уравнение плоскости, проходящей через
точку M0 с заданным вектором нормали
Направляющие векторы плоскости
Два неколлинеарных вектора, параллельных плоскости, назовем направляющими векторами плоскости
Параметрические уравнения плоскости
 – параметрическое уравнение плоскости
в векторном виде
– параметрическое уравнение плоскости
в векторном виде
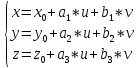 – параметрическое уравнение плоскости
в координатах
– параметрическое уравнение плоскости
в координатах
Уравнение плоскости через заданную точку и два направляющих вектора

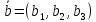
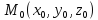 –фиксированная
точка
–фиксированная
точка
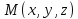 –просто точка лол
–просто точка лол
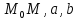 –компланарные,
значит их смешанное произведение равно
0.
–компланарные,
значит их смешанное произведение равно
0.
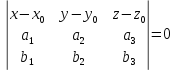
Уравнение плоскости, проходящей через три заданные точки

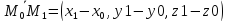

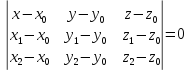 – уравнение плоскости через три точки
– уравнение плоскости через три точки
Уравнение плоскости в отрезках

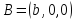

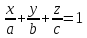 – уравнение плоскости в отрезках
– уравнение плоскости в отрезках
Доказательство
Для
доказательства воспользуемся тем, что
наша плоскость проходит через A,B,C,
а нормальный вектор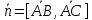

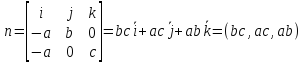
Подставим
координаты точки
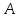 и вектораnв уравнение
плоскости с нормальным вектором
и вектораnв уравнение
плоскости с нормальным вектором
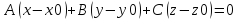
Получим

Или
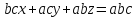
Разделим
все на
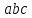 и получим
и получим
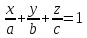
Такие дела.
Нормальное уравнение плоскости

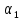 – угол междуoxи нормальным
вектором к плоскости, выходящим из О.
– угол междуoxи нормальным
вектором к плоскости, выходящим из О.
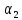 – угол междуoyи нормальным
вектором к плоскости, выходящим из О.
– угол междуoyи нормальным
вектором к плоскости, выходящим из О.
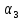 – угол междуozи нормальным
вектором к плоскости, выходящим из О.
– угол междуozи нормальным
вектором к плоскости, выходящим из О.
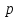 – расстояние от начала координат до
плоскости.
– расстояние от начала координат до
плоскости.
Доказательство или какая-то такая хуйня
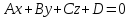
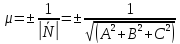
Знак противоположен D.

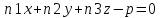

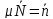

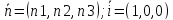
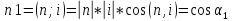
Аналогично для остальных косинусов. Конец.
Расстояние от точки до плоскости
Теорема
Точка S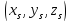 ,
плоскость
,
плоскость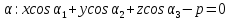
 – ориентированное расстояние от точкиSдо плоскости
– ориентированное расстояние от точкиSдо плоскости
Если
 ,
тоSи О лежат по разные
стороны от плоскости
,
тоSи О лежат по разные
стороны от плоскости
Если
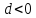 ,
тоSи О лежат по одну
сторону
,
тоSи О лежат по одну
сторону
 ,
умножаем наn
,
умножаем наn



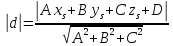
Взаимное расположение двух прямых в пространстве

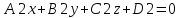
Коллинеарны

Совпадают

Пересекаются
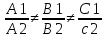
Угол между плоскостями
При пересечении образуется две пары вертикальных двухгранных углов, наименьший называется углом между плоскостями

Прямая в пространстве
Прямая в пространстве может быть задана как
Пересечение двух плоскостей:
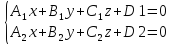

Параметрические уравнения прямой
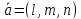
 – параметрическое уравнение прямой в
векторном виде
– параметрическое уравнение прямой в
векторном виде
 – параметрическое уравнение прямой в
координатах
– параметрическое уравнение прямой в
координатах
Каноническое уравнение
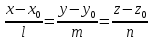 – каноническое уравнение прямой.
– каноническое уравнение прямой.
Уравнение прямой, проходящей через две заданные точки
1 вариант:
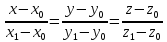
2 вариант: подставим в
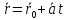 выражение
выражение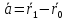

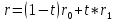 – каноническое уравнение прямой в
векторном виде;
– каноническое уравнение прямой в
векторном виде;
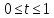
Взаимное расположение двух прямых в пространстве
Коллинеарны
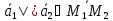
Совпадают
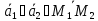
Пересекаются
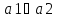 ;
;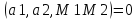
Скрещиваются
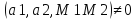
Взаимное расположение прямой и плоскости в пространстве
Параллельны. Нормальный вектор плоскости перпендикулярен прямой
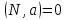
Прямая принадлежит плоскости.
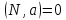 ,
а при подстановке координат точки в
общее уравнение прямой все должно быть
заебок.
,
а при подстановке координат точки в
общее уравнение прямой все должно быть
заебок.Пересекаются.
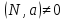
Угол между прямой и плоскостью
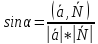
Расстояние от точки до прямой в пространстве
a– направляющий вектор нашей прямой.
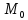 – произвольная точка, принадлежащая
данной прямой
– произвольная точка, принадлежащая
данной прямой
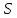 – точка, до которой ищем расстояние.
– точка, до которой ищем расстояние.

Расстояние между двумя скрещивающимися прямыми
a1 – направляющий вектор первой прямой
М1 – точка, принадлежащая первой прямой
а2 – направляющий вектор второй прямой
М2 – точка, принадлежащая второй прямой
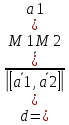
Расстояние между двумя параллельными прямыми
a1 – направляющий вектор первой прямой
М1 – точка, принадлежащая первой прямой
а2 – направляющий вектор второй прямой
М2 – точка, принадлежащая второй прямой
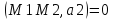
Кривые и поверхности второго порядка
Эллипс
Эллипсом назовем множество точек плоскости, сумма расстояний от которых до двух заданных точек (фокусов) есть величина постоянная.
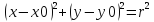
Каноническое уравнение эллипса


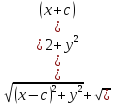




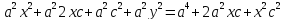
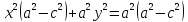
Заменим
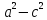 на
на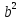

Разделим
на

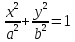
Свойства эллипса
Пересечение с осями координат
С ох:
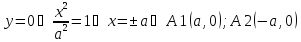
С оу:
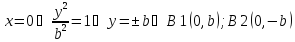
Симметрия относительно
Ох
Оу
Начала координат
Эллипс представляет собой кривую, лежащую в ограниченной части плоскости
Эллипс можно получить из окружности путем её растяжения или сжатия
Параметрическое уравнение эллипса:
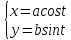
 – эксцентриситет
– эксцентриситет
 – директрисы
– директрисы
Гипербола
Гиперболой назовем множество точек плоскости, для которых модуль разности расстояний до 2х заданных точек (фокусов) есть величина постоянная(2a)

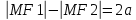
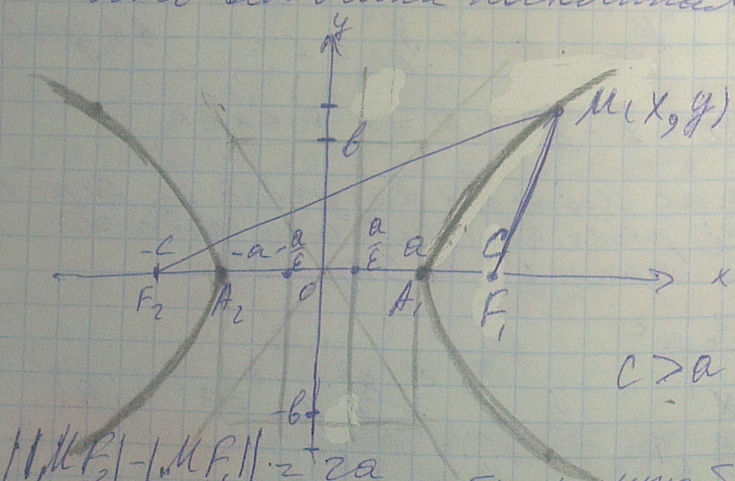
Делаем все то же самое, что и с эллипсом, получаем
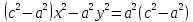
Заменяем
 на
на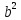
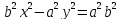
Делим на


Свойства гиперболы
Пересечение с осями координат
Ох:
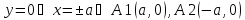
Оу: нету.
Симметрия:
Ох
Оу
Начало координат
Асимптоты гиперболы
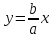 – первая асимптота
– первая асимптота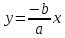 – вторая асимптота
– вторая асимптота
 ;
;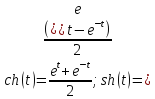
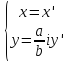 ; где
; где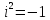
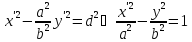
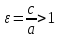 – эксцентриситет
– эксцентриситет
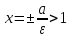 – директрисы
– директрисы
Асимптота
Асимптота – прямая, к которой кривая неограниченно приближается, удаляясь в бесконечность.
Парабола
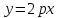
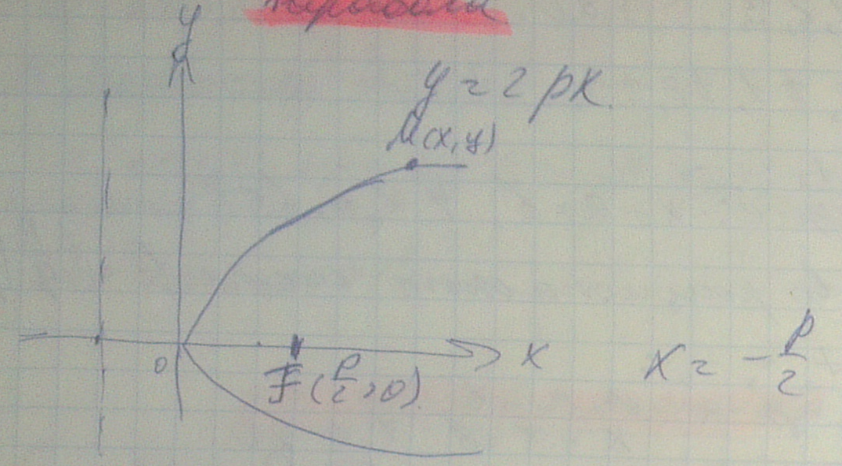
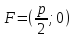
Свойства паработы
Пересечение с ох в (0,0)
Симметричность относительно ох
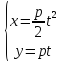

Родство эллипса, гиперболы и параболы.
Родство между этими кривыми имеет алгебраическое объяснение: все они задаются уравнениями второй степени. В любой системе координат уравнения этих кривых имеют вид: ax2+bxy+cy2+dx+ey+f=0, где a, b, c, d, e, f – числа
Преобразование прямоугольных декартовых систем координат
Параллельный перенос системы координат
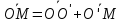
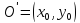 –O’
в старой системе координат
–O’
в старой системе координат
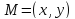 –координаты точки
в старой системе координат
–координаты точки
в старой системе координат
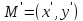 –координаты точки
в новой системе координат
–координаты точки
в новой системе координат
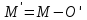 - координаты точки в
новой системе координат.
- координаты точки в
новой системе координат.
Поворот в прямоугольной декартовой системе координат
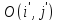 –новая система
координат
–новая система
координат
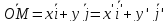
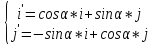
Матрица перехода от старого базиса к новому
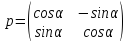 – (под первым столбцомI’,
под вторым –j’)
матрица перехода от базисаI,jк базисуI’,j’
– (под первым столбцомI’,
под вторым –j’)
матрица перехода от базисаI,jк базисуI’,j’
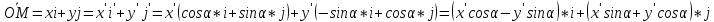
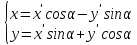
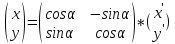
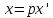
Общий случай
1 вариант
Параллельный перенос начала координат
Поворот системы координат
2 вариант
Поворот системы координат
Параллельный перенос начала координат
Общее уравнение линий второго порядка и его приведение к каноническому виду
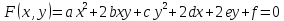 – общий вид уравнений кривой второго
порядка
– общий вид уравнений кривой второго
порядка
Пиздец
Классификация кривых второго порядка
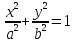 –Эллипс
–Эллипс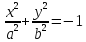 – Мнимый эллипс
– Мнимый эллипс – гипербола
– гипербола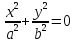 – пара мнимых пересекающихся прямых
– пара мнимых пересекающихся прямых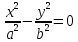 - пара пересекающихся прямых
- пара пересекающихся прямых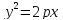 – парабола
– парабола – пара параллельных прямых
– пара параллельных прямых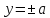
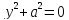 – пара мнимых параллельных прямых
– пара мнимых параллельных прямых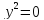 – пара совпадающих прямых
– пара совпадающих прямых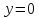
Эллипсоид
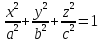
Сечения эллипсоида
Yoz, x=0
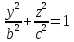 – эллипс
– эллипс
Xoz, y=0
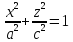 – эллипс
– эллипс
Xoy, z=h
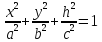
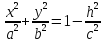
Если
 ,
то ничего
,
то ничегоЕсли
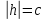 ,
то пара мнимых прямых
,
то пара мнимых прямыхЕсли
 ,
то эллипс
,
то эллипс
Эллипсоиды вращения
Эллипсоидами вращения являются либо сплющенные, либо вытянутые сфероиды, в зависимости от того, вокруг чего вращаем.
Однополосный гиперболоид
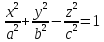
Сечения однополосного гиперболоида
Yoz, x=0
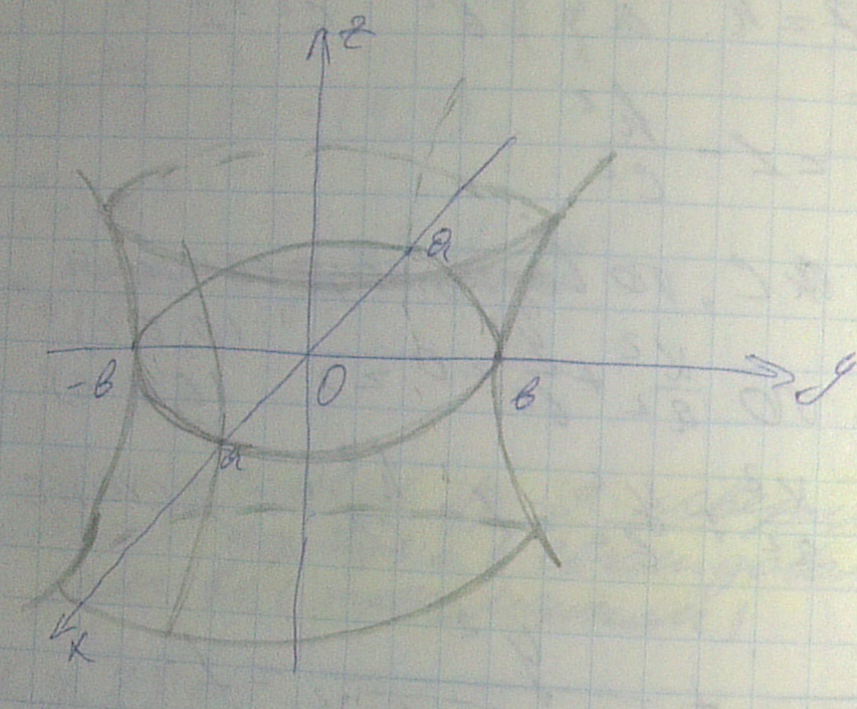
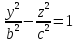 – гипербола с действительной осьюoy
– гипербола с действительной осьюoy
Xoz, y=0
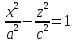 – гипербола с действительной осью ох
– гипербола с действительной осью ох
Xoy, z=h

Получается эллипс при любых h. Такие дела.
Однополосные гиперболоиды вращения
Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси.
Двуполостный гиперболоид
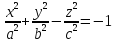
Сечения двуполостного гиперболоида
Yoz, x=0
 – гипербола с действ. Осьюoz
– гипербола с действ. Осьюoz
Xoz,y=0
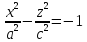 – гипербола с действительной осьюoz
– гипербола с действительной осьюoz
Xoy, z=h

 не существует
не существует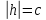 пара мнимых пересекающихся
пара мнимых пересекающихся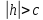
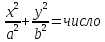 – эллипс.
– эллипс.
Конус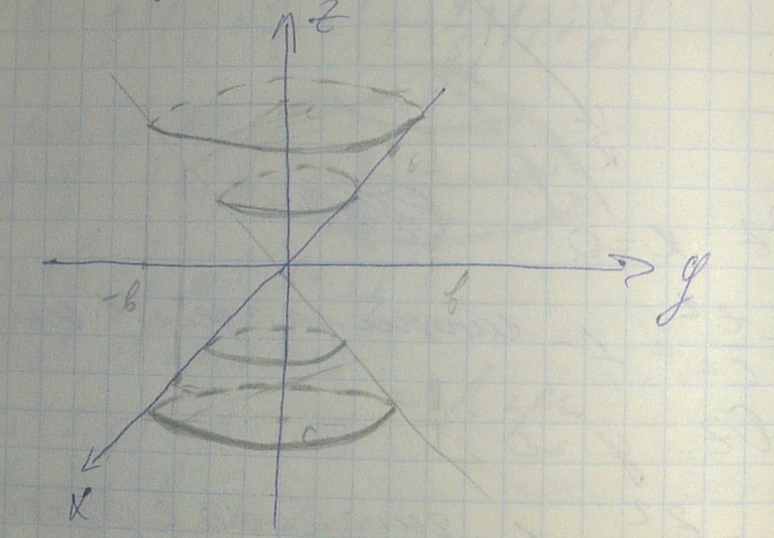
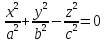
Yoz, x=0

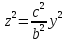
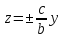 – пара пересекающихся прямых
– пара пересекающихся прямых
Xoz, y=0
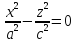
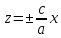 – пара пересекающихся прямых
– пара пересекающихся прямых
Xoy, z=h

h=0, получаем вершину конуса
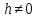 получаем расширение конуса с увеличением
модуляh
получаем расширение конуса с увеличением
модуляh
Эллиптический параболоид
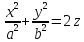
Сечения:
yoz, x=0
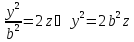 -
парабола
-
парабола
xoz, y=0
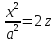 – парабола
– парабола
xoy, z=h
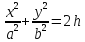
h<0 не существует
h=0 это точкаO(0,0,0)
h>0 эллипс с полуосями
 ,
,
Вращения
Если 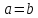 , то
эллиптический параболоид представляет
собой поверхность вращения, образованную
вращением параболы вокруг её оси
симметрии.
, то
эллиптический параболоид представляет
собой поверхность вращения, образованную
вращением параболы вокруг её оси
симметрии.
Гиперболический параболоид


Сечения
yoz, x=0

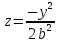 -
парабола
-
парабола
xoz, y=0
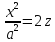
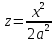 – парабола
– парабола
xoy, z=h
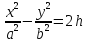
h=0
h>0 гипербола с действительной осью параллельной ох
h<0 гипербола с действительной осью паралльной оу и мнимой ох
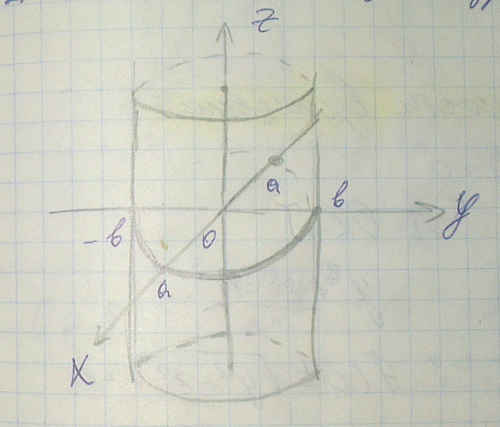
Цилиндр
Под цилиндром будем понимать поверхность, которая будет получаться при движении прямой в пространстве, не меняющая своего направления, если прямая движется относительно oz, то уравнение цилиндра есть уравнение сечения плоскостьюxoy.
Эллиптический цилиндр
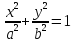
Гиперболический цилиндр
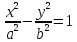

Параболический цилиндр
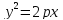

Прямолинейные образующие поверхностей второго порядка
Прямые, полностью лежащие на поверхности, называются прямолинейными образующими поверхности.
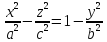

1я прямая:
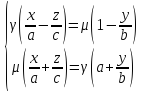
2я прямая
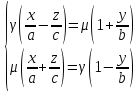
Поверхности вращения
Ебать ты лох
Отображение
Отображениемназовем правило, по которому каждому элементу множества А ставится в соответствие один или несколько элементов множестваB. Если каждому ставится единственный элемент множества В, то отображение называетсяоднозначным, иначемногозначным.
Преобразованиеммножества называется взаимнооднозначное отображение множества на себя
Инъекция
Инъекция или взаимно-однозначное отображение множества А на множество В
(разным элементам а соответствуют разные элементы В) например y=x^2
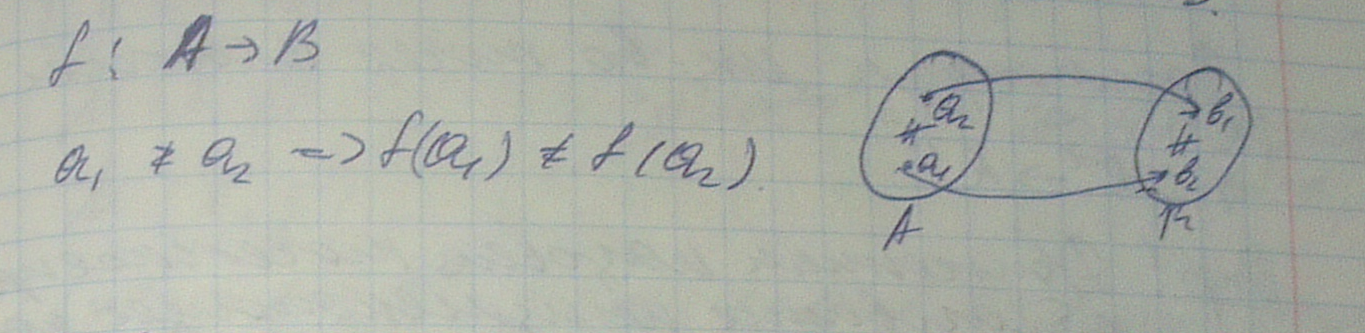
Сюръекция
Сюръекция или отображение множества А на множество В
Для каждого В существует хотя бы одно А(например синус)
Биекция
Каждому элементу множества В соответствует только один элемент множества А.(например y=x)