Лекции - Структуры и алгоритмы компьютерной обработки данных / 11.Деревья поиска. Случайные (рандомизованные) бинарные деревья

Двоичные деревья

Подобно элементам списка, узлы дерева будем представлять записями, содержащими некоторую информацию и два указателя left и right - на корни левого и правого поддерева соответственно. Ссылки на пустые поддеревья будут обозначаться значением nil. Отдельная переменная T:PNode будет указывать на корень дерева.

Type PNode=^Node;

Node = record

Data: DataType;

left,right: PNode;

end;

Представление произвольных деревьев

Любое произвольное дерево может быть представлено в виде двоичного. При этом левая ссылка в каждом узле указывает на потомка узла, а с помощью правой ссылки все потомки одного узла связываются в список.

Деревья поиска

Для хранения и поиска данных обычно используются двоичные деревья поиска. Двоичное дерево называется деревом поиска, если для каждой вершины ti справедливо утверждение, что все ключи левого поддерева ti меньше ключа ti, а все ключи правого поддерева ti больше его.

В дереве поиска можно найти элемент с заданным ключом - достаточно, начав с корня, двигаться к левому или правому поддереву на основании сравнения с ключом текущей вершины.

Способы обхода дерева

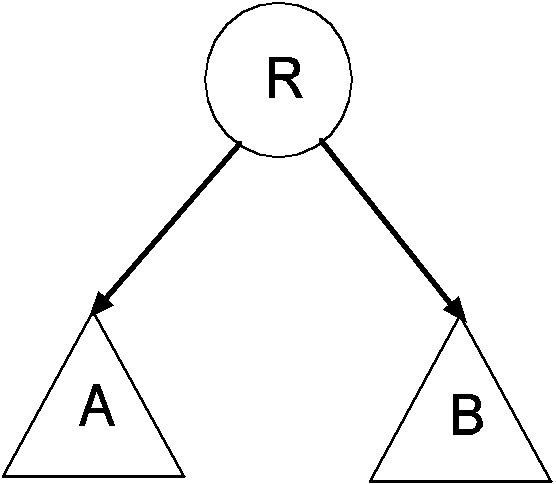
• Сверху вниз: R, А, В (корень посещается ранее, чем поддеревья).

• Слева направо: А, R, В.

• Справа налево: B, R, A.

• Снизу вверх: А, В, R (корень посещается после поддеревьев).

Процедура обхода дерева

Procedure Visit(T:PNode);

begin

if T<> nil then

begin

Visit(T^.left);

Write(T^.data,' ');

Visit(T^.right);

end

end;

Обход дерева поиска слева направо и справа налево перебирает узлы в отсортированном порядке.

Добавление в дерево

Для этого заметим, что если дерево пусто, то элемент ставится в его вершину. Если дерево непусто, то можно сравнить добавляемый ключ с ключом в вершине и рекурсивно добавить элемент в левое или правое поддерево.

Сложность - Ө(H), где H – высота дерева.

В худшем случае, если данные изначально упорядочены, например по возрастанию, вставка будет производиться всегда в правое поддерево. В результате полученное дерево будет являться фактически линейным списком. Сложность будет линейная.

Сбалансированные деревья

Высота будет минимальной Ө(log n), если для каждого узла количество узлов в левом и правом поддереве отличается не более чем на единицу. Такое дерево называется идеально сбалансированным.

Существует много способов добиться приближенной сбалансированности. Наиболее известны АВЛ-деревья, предложенные Г.М. Адельсоном-Вельским и Е. М. Ландисом; красно-черные деревья; 2-3 деревья, разработанные Хопкрофтом. Во всех предложенных структурах поиск производится так же, как в деревьях двоичного поиска, а при добавлении и удалении с помощью специальных операций, называемых вращениями, производится перестройка дерева с целью добиться лучшей сбалансированности.

Рандомизованные деревья

При добавлении в дерево данных, упорядоченных случайным образом, получается дерево, близкое к сбалансированному.

При добавлении в рандомизованное дерево мы используем генератор случайных чисел для моделирования случайного порядка исходных данных.

Так, если в дерево добавляeтся n элементов, то вероятность для каждого элемента оказаться при случайном упорядочении первым и попасть в корень дерева равна 1/n. В рандомизованном дереве мы с такой вероятностью помещаем элемент в корень дерева.

Описание узла дерева

Для определения вероятности требуется знать количество элементов в каждом поддереве. Будем хранить это количество в корне поддерева в поле N и изменять при добавлении и удалении элементов.

Type TTree = ^TNode;

TNode = Record

X: Longint;

L,R: TTree;

N: Word;

end;

Определение количества элементов в поддереве

Для определения количества элементов в поддереве напишем функцию GetN, которая правильно работает и для пустого дерева

Function GetN(T:TTree):longint;

begin

if t = Nil then GetN:=0

else GetN:=T^.N

end;

Вставка в корень

Далее необходимо написать процедуру для вставки элемента в корень дерева. Процедура будет рекурсивной: для пустого дерева она просто создаст новый узел, для непустого - рекурсивно добавит узел в корень левого или правого поддерева, а затем выполнит левое или правое вращение

Левое вращение

Пусть узел добавлен в корень левого поддерева и его нужно вытащить в корень дерева. Обозначим указатель на корень дерева T, на корень поддерева - - S. Для того, чтобы дерево оставалось деревом двоичного поиска, правое поддерево S стало левым поддеревом T.

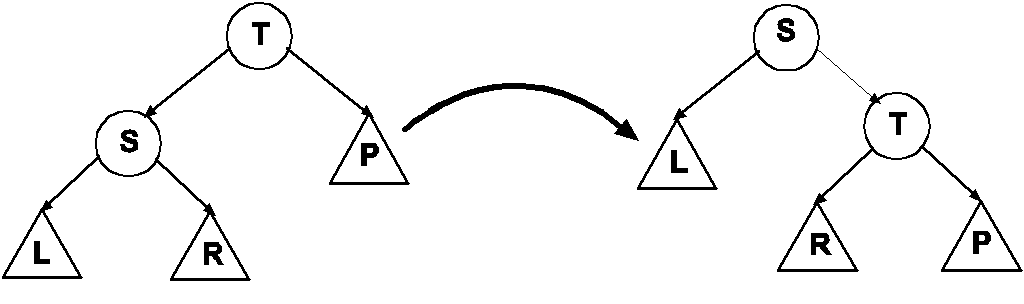
Процедура вращения

Процедура левого вращения с обновлением поля N выглядит так:

Procedure RotL(var T:TTree);

Var S:TTree;

N1,N2:longint;

begin

S:=T^.L;

N1:=GetN(T); N2:=GetN(S^.r)+GetN(T^.r)+1;

T^.L:=S^.R; S^.R:=T;

S^.n:=N1; T^.n:=N2;

T:=S

end;

Аналогично выглядит процедура правого вращения RotR

Процедура добавления в корень

Procedure AddRoot(var T:TTree; X:longint);

begin

if T = Nil then

begin

New(T);

T^.X:=X; T^.L:=Nil; T^.R:=Nil; T^.n:=1;

end

else

if T^.X>X then

begin AddRoot(T^.L,X); INC(t^.n); RotL(T) end

else

begin AddRoot(T^.R,X); INC(t^.n); RotR(T) end

end;

Процедура добавления

Процедура добавления элемента Add будет вызывать добавление в корень с вероятностью 1/n. Для этого вычисляется случайное число от 0 до n и добавление в корень происходит, если оно равно 0.

Procedure Add(var T:TTree; X:longint);

begin

if Random(GetN(T)+1) = 0 then AddRoot(T,X)

else

begin

if T^.X>X then Add(T^.L,X) else Add(T^.R,X);

INC(t^.n);

end;

end;

Удаление элемента

Удаление элемента в рандомизованном дереве также должно сохранять сбалансированность. Если одно из поддеревьев содержит больше элементов, то разумно, чтобы элемент для замены удаляемого извлекался с большей вероятностью именно из этого поддерева.

Удаление в рандомизованном дереве основано на операции объединения деревьев. После удаления элемента мы должны объединить его левое и правое поддеревья.

Объединение деревьев

Объединение деревьев выполняется рекурсивно. Если одно из деревьев пусто, то результат объединения равен другому дереву. Если оба дерева непусты, то мы в корень объединенного дерева помещаем либо корень левого дерева и присоединяем справа объединение его правого поддерева и второго дерева, либо корень правого дерева и аналогично другое дерево присоединяем слева

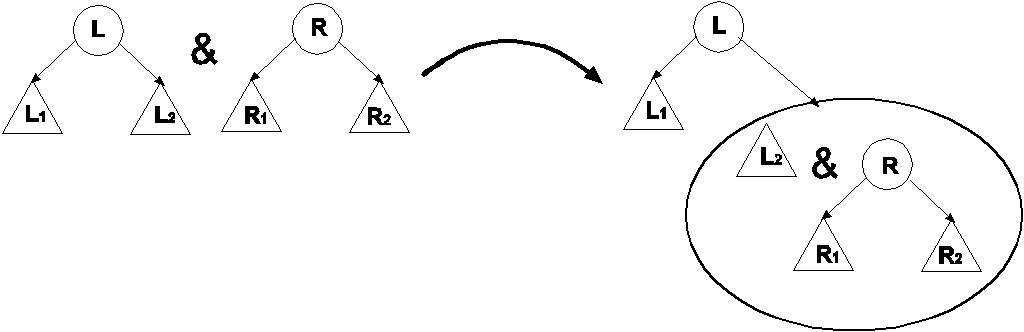
Функция объединения деревьев

Пусть левое дерево содержит N1 узлов, а правое N2 узлов.

Function Join(L,R:TTree):TTree;

Var N:integer;

begin

if R=Nil then Join:= L else if L=Nil then Join:= R

else

begin

N:=GetN(R)+GetN(L);

if Random(GetN(L)+GetN(R)+1)<GetN(L) then

begin L^.R:=Join(L^.R,R); L^.N:=N; Join:=L; end

else begin R^.L:=Join(L,R^.L); R^.N:=N; Join:=R; end

end

end;

Удаление элемента

Теперь не составляет труда записать процедуру удаления элемента с ключом X из рандомизованного дерева. Логический параметр P нужен для сохранения информации о том, что элемент найден, чтобы скорректировать количество элементов в вышестоящих узлах.

Процедура удаления

procedure Delete (Var T:TTree;X:Longint; Var P:boolean);

Var S:TTree;

begin

P:=False;

IF T<> Nil then

if X<T^.X then

begin Delete (T^.L,X,P); if P then Dec(T^.N) end

else if X>T^.X then

begin Delete (T^.R,X,P); if P then Dec(T^.N) end

else if X=t^.X then {найден элемент для удаления}

begin

S:=T; T:=Join(T^.L,T^.R);

Dispose(S); P:=True;

end;

end;

Анализ рандомизованных деревьями

Операции добавления, удаления и поиска имеют сложность Ө(log n).

С той же сложностью могут выполняться операции поиска максимального, минимального элемента, определения количества элементов, имеющих ключи меньше или больше данного