Otvety_KhTP

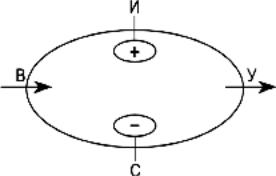
В (вход) – количество субстанции, входящей снаружи в систему на протяжении выбранного интервала времени; У (уход) – количество субстанции, уходящей за тот же интервал наружу; И (источник) – количество субстанции, возникающей (образующейся) за интервал времени внутри системы; С (сток) – количество субстанции, исчезающей (расходуемой) внутри системы за тот же интервал.

Пятая статья баланса – накопление Н – на схеме не обозначена. В каждый момент внутри системы находится какое-то количество субстанции. Накопление – это его приращение за интервал времени, разность между количеством субстанции в системе к концу интервала и количеством, которое было в начале.

Накопление может быть положительным (количество субстанции увеличилось), отрицательным (ее количество уменьшилось) и равным нулю (к концу интервала оно такое же, как было в начале).

Встационарном процессе накопление равно нулю. Общий вид уравнения баланса:

В+ И – (У + С) = Н

Вслучае стационарного процесса Н = 0 и уравнение получает вид

В+ И – (У + С) = 0

Математическое описание химических процессов в большинстве случаев состоит из уравнений баланса – прежде всего материального и теплового. Значения отдельных статей баланса обусловлены закономерностями процесса. Вход вещества определяется расходом входящего потока и концентрацией данного вещества в нем; вход тепла зависит от энтальпии входящей жидкости, ее расхода и от передачи тепла снаружи через стенки. Источники и стоки тепла и вещества пропорциональны скоростям реакций в рабочей зоне и т.д. Какими уравнениями будет описан процесс – зависит от выбора

контура и интервала времени, а те в свою очередь – от особенностей потоков в рабочей зоне и стационарности или нестационарности процесса.

11.Понятие стационарности для химического реактора.

Стационарный процесс. Его параметры не меняются во времени, поэтому время как переменная исчезает из описания. Стационарные процессы непрерывны, а значит, они обязательно проходят в открытых системах, т. е. системах, обменивающихся веществом с окружающей средой. Именно этот обмен – ввод исходных материалов и вывод продуктов – и поддерживает непрерывность. В аппарате, в котором идет непрерывный процесс, обязательно движется поток.

Нестационарные процессы характеризуются изменением параметров во времени. Нестационарными являются все периодические процессы. Кроме того, нестационарно может работать и аппарат непрерывного действия. Это происходит во время переходных процессов, заключающихся в переходе от одного стационарного режима к другому. Переходные процессы возникают при пуске, остановке, переналадке режима, а также вследствие случайных возмущений – колебаний процесса под воздействием неконтролируемых факторов.

Нестационарный процесс может протекать как в замкнутой системе, не обменивающейся веществом с окружающей средой (например, в автоклаве), так и в открытой системе (периодическая ректификация, переходный процесс в аппарате непрерывного действия и т. д.).

В некоторых случаях один и тот же процесс можно описать и как стационарный, и как нестационарный – в зависимости от системы переменных, в которой проводится описание.

12.Проектный и поверочный расчет оборудования.

Проектным расчетом называют такой, цель которого состоит в определении требуемых размеров аппарата, при которых могут быть достигнуты заданные показатели.

Поверочным расчетом называют такой, в котором мы задаемся размерами аппарата и находим, какие показатели могут быть при этом достигнуты. Во многих случаях целесообразно свести проектный расчет к совокупности поверочных: задаться рядом типоразмеров аппаратов, для каждого из них

рассчитать достижимые показатели, после чего выбрать наилучший размер. Особенно простой такая процедура получается при использовании компьютера.

13.Прямая и обратная задача для математической модели.

Общий вид уравнения математической модели может быть представлен как: yi = Fi (X,B)

где B = (b0, b1,…., bp) – вектор параметров.

Такая запись отражает тот факт, что в модель обязательно входят параметры. Возможны два основных класса задач, связанных с уравнениями данного вида.

Задача первого класса. Нам заданы X, В. В этих условиях следует определить yi. Это прямая задача. В такой формулировке она сводится к расчету функции, заданной в явной форме. Если рассмотреть переменные Х, то решение данной задачи дает изменение величины y, или распределение y в пространстве факторов.

Задача второго класса. Нам задано распределение (как правило, в виде совокупности экспериментальных данных) y в пространстве факторов X и известен общий вид функции. Требуется определить параметры b0, ..., bр. Это обратная задача.

14.Параметрическая чувствительность модели.

В ряде случаев анализ математической модели позволяет обнаружить такие особенности процесса, предсказание которых по лабораторным данным

невозможно или весьма затруднительно, поскольку они сильно зависят от размеров объекта.

Параметрическая чувствительность Пij – производная от i-й выходной величины по j-му входному параметру:

Чем больше Пij , тем сильнее влияет данный фактор на выход. Если параметрическая чувствительность очень мала, то соответствующим фактором нельзя пользоваться как управляющим: он почти не влияет на процесс. Если параметрическая чувствительность чрезмерно велика, процесс становится трудноуправляемым. Даже малые колебания входного параметра приводят к резким колебаниям режима.

Поэтому приходится либо чрезвычайно точно стабилизировать вход, либо тем или иным способом снижать чувствительность.

Отмечу, что поскольку Пij — функция входных факторов, то при их изменении процесс может попадать в области и малой, и высокой чувствительности.

В ряде случаев параметрическую чувствительность целесообразно определять, заменяя в уравнении производную отношением малых конечных приращений

Предельный случай параметрической чувствительности: П → ∞. Это означает, что бесконечно малое изменение входного параметра вызывает конечное изменение показателей работы. Такая ситуация наблюдается при неустойчивости процессов.

15.Адекватность модели экспериментальным данным.

Адекватность означает насколько точно с точки зрения целей моделирования, полученные на основе испытания построенной модели результаты, отражают истинное состояние оригинала. При оценке адекватности в случае сложных систем исходный вариант модели подвергают следующим проверкам:

•все ли существенные параметры учтены в модели;

•нет ли в модели несущественных параметров;

•правильно ли определены ограничения на значения параметров;

•не дает ли модель абсурдные ответы, если ее параметры будут принимать предельные значения;

•не противоречива ли модель сама по себе;

•подчиняется ли законам математической логики.

В целом можно говорить об адекватности модели оригиналу, если:

1)поведение модели достаточно точно совпадает с поведением моделируемого объекта в одинаковых ситуациях;

2)модель убедительно представлена относительно тех свойств объекта,

которые прогнозируются с помощью модели.

Проведение любого модельного эксперимента всегда сопряжено с наличием погрешности в результатах, чему имеется множество причин, каждую из которых можно отнести к одной из двух групп.

Первая группа причин состоит в неизбежной неопределенности постановки задачи, связана с неполнотой исходной информации и порождает так называемую случайную погрешность, которую при проведении экспериментов невозможно оценить, не привлекая дополнительную информацию.

Вторая группа причин является следствием принятия различных допущений и ограничений при разработке концептуальных моделей и формализации системы, а также преднамеренного снижения сложности математических моделей и в результате приводит к возникновению систематической погрешности.

16.Однозначность определения параметров модели по данным эксперимента.

Чаще всего простота или сложность математической модели связаны с тем, сколько в нее входит параметров – коэффициентов, учитывающих те или иные особенности объекта.

Значения параметров характеризуют свойства данного конкретного объекта, отличающие его от других объектов того же класса. Чем больше параметров входит в модель, тем подробнее удается охарактеризовать его и тем точнее описать.

На одном полюсе здесь выступают предельно идеализированные модели, такие, как идеальный газ, абсолютно упругое тело и др.

Уравнения при этом либо вообще не содержат параметров, включая лишь универсальные константы (идеальный газ), либо их число минимальное (модуль упругости в законе Гука). Эти идеализированные модели почти полностью игнорируют конкретные свойства объектов.

На другом полюсе — сложные многопараметрические модели, учитывающие много конкретных свойств. Так как мы всегда хотим иметь максимально точное описание объекта, с этой точки зрения сложные модели обладают несомненными преимуществами.

Но у сложных моделей есть и недостатки. Прежде всего такую модель трудно обрабатывать.

Еще одна трудность, связанная с применением многопараметрических моделей, — это чувствительность к ошибкам опытов. Чем больше параметров, тем более точный эксперимент требуется, чтобы достаточно хорошо оценить эти параметры. Если модель построена на основе структурного подхода, а эксперимент не очень точен, то возникает специфическая опасность потери физического смысла.

Еще одна отрицательная особенность многопараметрических моделей: ненадежность экстраполяции. Уравнение, которое хорошо описывает объект в области, изученной экспериментально, становится крайне неточным уже при небольшом выходе за ее пределы. Разумеется, та же особенность присуща и чисто эмпирическим моделям.

Основной вывод из сказанного: если необходима высокая точность описания, следует применять многопараметрические модели, но при этом эксперимент должен отличаться высокой точностью и большим объемом. Если же требования не столь велики, чаще всего целесообразно использовать простейшую из моделей, обеспечивающих нужную точность. Впрочем, в конкретных случаях требуется конкретное рассмотрение. Бывает и так, что из двух возможных моделей мы выберем несколько более сложную, зато более ясную

физически. Дать непогрешимый рецепт на все случаи жизни невозможно.

17.Однозначность определения структуры модели по данным эксперимента.

Проводят эксперимент и по зависимости выходным данных от входных выводят эмпирическое уравнение, считают адекватность модели по критерию Фишера и далее пытаются представить структуру модели по зависимости выхода от входа. Может быть несколько структур описывающих систему.

18.Стехиометрическая матрица реакции, применение.

Если кратко:

Есть некая система уравнений – это система однородных уравнений 1-й степени (однородные – такие, у которых свободные члены равны нулю. И такая система может быть полностью охарактеризована матрицей коэффициентов. Детерминант =0, матрица вырожденная, если не равен – то невырожденная. Правило Гиббса. Первое: Если стехиометрический коэффициент какого-то вещества отличен от нуля только в одной из стадий, эта стадия независима и ее можно вычеркнуть. Второе: После такого вычеркивания для оставшихся стадий продолжает действовать первое правило, пока не останется лишь одна стадия, либо пока для немногих оставшихся стадий не удастся установить линейную зависимость. Применения: позволяет убирать не ключевые вещества, рассчитать значения концентраций на основе матрицы, вычисление скоростей изменения концентраций реагентов и продуктов

А, В, С, … или А1, А2, А3, … – символы веществ; а1, а2, а3, … – соответствующие стехиометрические коэффициенты.

19.Ключевые и неключевые реактанты в задачах по стехиометрии реакции.

Те вещества, количества которых в данный момент заданы, называют ключевыми , а те, количества которых мы рассчитываем, – неключевыми . Заметим, что для начального момента должны быть известны количества и тех, и других веществ. Любое из веществ, участвующих в реакции, может выступать в роли и ключевого, и неключевого. Чаще всего ключевыми оказываются те вещества, количества (или концентрации) которых проще измерить.

20.Химическая переменная, применение в задачах по стехиометрии реакций.

21.Степень превращения,выход,селективность,эквивалент