Otvety_KhTP

(2)

После этого делаем шаг в точку 2 для следующего расчета F. Ее координаты находятся так:

(3)

причем

(4)

Здесь i – номер точки; j – номер фактора.

Дальше можно действовать по-разному. Можно определить производные в новой точке i + 1, найти новое направление градиента, сделать шаг и т. д. Но чаще поступают иначе. Если шаг оказался удачным, т. е. если Fi+1 > Fi (при поиске максимума), то делают следующий шаг в том же направлении, подставляя в формулу (4) ранее найденные значения производных. Практически наверняка это будет уже не направление градиента: его направление в разных точках пространства факторов – разное, если только функция F не является линейной. Но можно надеяться, что еще один шаг в прежнем направлении снова даст приращение F нужного знака, хотя и не максимально возможное (так как от градиента мы отклонились). Зато мы сэкономим на том, что не будем лишний раз рассчитывать производные. Если и этот шаг удачен, шагнем еще раз и т. д.

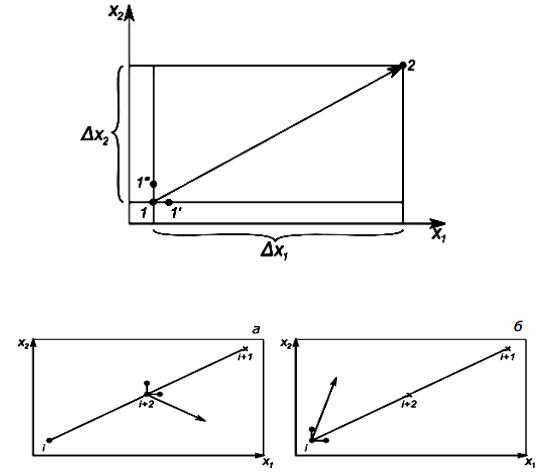
Рис. 2. Схема расчетов в методе градиента

Рис. 3. Схема расчета после неудачного шага

Что делать, когда шаг неудачен? Что это может означать? Очевидно, поверхность настолько искривлена, что данное направление перестало вести нас вверх, мы «перескочили» через ту окрестность предыдущей точки, в которой функция возрастала. Поэтому в таком случае обычно уменьшают шаг, например вдвое. Теперь, если уменьшенный шаг в том же направлении будет удачен, нет смысла делать еще шаг, поскольку он приведет в «плохую» точку (см. рис. 3, а: крестик – неудачный шаг, (i + 2) – точка половинного шага). В этом случае около точки (i + 2) поставим вспомогательные точки для расчета производных по формуле (2), найдем новое направление градиента и двинемся по нему (на рис. 3 вспомогательные точки – черные кружки, новое направление градиента – стрелка). Если же и уменьшенный шаг не приведет в «хорошую» точку (рис. 3, б), то вернемся в точку i и будем в ней искать направление градиента. Движение продолжаем до тех пор, пока шаги не станут очень малыми. Уменьшение шагов объясняется двумя причинами: первая –неоднократным уменьшением в тех случаях, когда большой шаг оказывался неудачным; вторая – это принципиально важнее, – то, что вблизи оптимума производные

близки к нулю и формула (4) дает уже очень малые приращения. Для останова∆xijвычисленийокажутсяменьше,ожно использоватьчем соответствующиемомент, когдамалыеоба

величиныприращенияεj.

40. Ограничения при оптимизации, их виды и роль.

Как бы хорошо ни был выбран критерий оптимальности, в большинстве задач этого недостаточно, чтобы учесть все условия, в которых должен проходить процесс. С одной стороны, как уже отмечалось, нас всегда интересует не один результат процесса, а

многие. С другой – слишком редко удается реализовать все значения входных параметров, которые желательны. Условия, которые необходимо соблюдать независимо от того, как их соблюдение повлияет на величину критерия оптимальности, называют ограничениями.

В самом общем виде можно назвать две основные причины возникновения ограничений.

Первая: ограничения – «несостоявшиеся» критерии оптимальности. Я уже говорил, что в большинстве случаев вначале у нас есть много показателей, которые могли бы претендовать на роль критерия оптимальности, но выбрать можно лишь один из них. Тогда по остальным мы устанавливаем ограничения. Например, в качестве критерия можно выбрать затраты на проведение процесса, а величины степени разложения, концентрации кислоты и качества фильтрации задать в форме ограничений.

Вторая причина – учет наших возможностей. Мы не можем задать температуру выше той, которую выдержит наш аппарат, использовать катализатор с активностью, большей, чем имеющаяся у нас партия, и т.д. Более подробный анализ указывает на следующие группы ограничений:

• по количеству и качеству сырья и продукции – состав сырья, как правило, задается не нами и менять его нельзя; количество сырья также может быть ограничено; выпуск продукции не должен быть больше того, что можно реализовать; качество продукта не должно быть ниже стандарта или требований заказчика;

• по условиям технологии – расход воздуха не может превышать производительность вентилятора; температура не может быть выше предела, при котором портится материал аппарата или катализатор; размеры аппаратов изменять мы не можем и т. д.;

• по экономическим и конъюнктурным соображениям –

капитальные затраты не должны превышать выделенной суммы; срок ввода нового производства не должен быть позже запланированного; нельзя применять методы и устройства, защищенные чужими патентами;

• по соображениям охраны труда и окружающей среды – это чрезвычайно важная группа ограничений, жесткость которых все возрастает.

Кроме классификации по смыслу ограничения можно различать по формально-математическим признакам. Так, выделяют ограничения типа равенств и типа неравенств.

Ограничения типа равенств устанавливают определенное значение того или иного параметра:

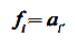(1)

Здесь fi– один из параметров, аi– задаваемое для него значение.

Например, в конкретных условиях работы задаются численные значения, характеризующие состав сырья, размеры аппаратов, нагрузку на аппарат и т. д.

Ограничения типа неравенств определяют пределы, в которых допустимо изменение параметров процесса:

(2)

Два первых ограничений (2) задают односторонние пределы (например, производительность не ниже заданной; температура не выше той, на которую рассчитан материал). Третье ограничение – двустороннее (например, температура жидкости в пределах от температуры замерзания до температуры кипения).

Наконец, в расчетных процедурах нахождения оптимума большую роль играет деление ограничений по следующему признаку: ограничения 1-го рода – условия (1) или (2), где в качестве параметров f фигурируют входные факторы; ограничения 2-го рода, где параметрами служат различные функции входов, например результаты процесса или, скажем, температуры в каких-то точках внутри аппарата. Когда при математическом решении задачи рассматривается какой-либо режим, то он задается значениями входов. При этом вопрос о том, не нарушены ли какие-либо ограничения 1-го рода, проверяется непосредственно. А для проверки соблюдения ограничений 2-го рода необходимо сначала рассчитать соответствующие параметры, что может осложнить расчет.

41. Численные методы однофакторной оптимизации.

Когда F зависит только от одного фактора, F= F(x): тогда говорят об одномерном поиске.

Численные методы однофакторной оптимизации:

1) оптимизация перебором

Метод сканирования (также подходит для многофакторной оптимизации)

2)Метод деления пополам

3)Метод золотого сечения (смотреть вопросы 42,43,44)

42. Метод сканирования (одномерная оптимизация).

Сканирование – метод, близкий к перебору, но применяемый к непрерывным функциям. Рассмотрим для примера одномерное сканирование – случай, когда ищется максимум функции от одного фактора (как я уже говорил, поиск минимума осуществляется точно так же). Будем считать, что мы задались пределами изменения фактора х от а до b. Здесь а и b – ограничения, которые можно установить в любой реальной задаче: никогда не бывает так, что мы может задать любые, ничем не ограниченные значения х.

Таким образом имеется интервал [а, b], на котором мы хотим отыскать экстремум целевой функции; его называют интервалом неопределенности. При этом практически нам не нужно определять точку экстремума абсолютно точно. Достаточно сильно сузить интервал неопределенности. Например, если мы узнаем, что оптимальная температура, соответствующая максимуму целевой функции, заключена в пределах от 380 до 381 К, то большая точность не нужна. В промышленных условиях вряд ли удастся регулировать температуру с точностью выше 1 К. Нас устраивает интервал неопределенности [380, 381], и дальнейшее его сужение смысла не имеет.

Итак, в одномерном случае задача поиска экстремума сводится к сужению интервала неопределенности. Методом сканирования эта

задача решается следующим образом. Выбираем целое число q – число значений целевой∆x: функции, которое придется рассчитывать. Находим интервал

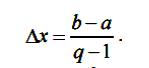(1) ∆х (рис. 1). Концы каждогоОткладываеминтервалаот точкиназовемдо точкиузлами;b интервналырис. 1 каждый узел обозначен крестиком.

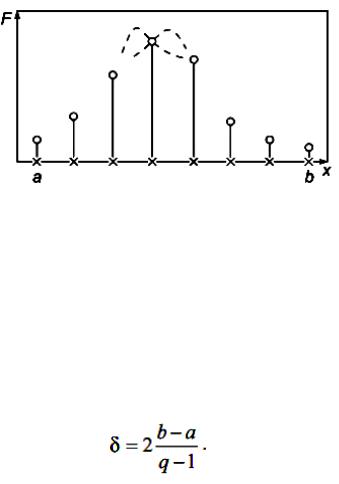
Рис. 1. Поиск экстремума сканированием: a, b – границы интервала неопределенности

В каждом узле рассчитываем F(х) (см. точки на рис. 1). Теперь мы

можем принять за максимум наибольшее из полученных значений

– на рисунке это 4-я точка слева∆х: истинный. К концу максимумр счета интервалможет лежатьн определибоенносправа,ти δ составитлибо слева2 от полученной наилучшей точки (штрихи на рис. 1). Таким образом,

(2)

Формула (2) определяет эффективность метода. При сканировании для достижения достаточно малого значения δ величина q должна быть велика. Метод малоэффективен, но удобен для первоначального исследования функции, поскольку дает возможность представить ее вид на всем отрезке, установить число экстремумов и их локализацию.

Более эффективно сканирование с переменным шагом: сократив интервал неопределенности, мы продолжаем∆х. Например,поиск внутридвигаясьэтогона интервала, уменьшая в свою очередь

рис. 1 от а к b и дойдя до 5-й слева точки, можно двинуться в обратном направлении меньшими шагами; затем эту процедуру можно продолжить, снова двигаясь вправо и снова уменьшив шаги и т.д. Такой вариант часто называют методом тяжелого шарика (если ищется минимум, то движение точек по кривой функции похоже на скатывание шарика в ложбину, когда он раз за разом проскакивает нижнее положение, колеблясь около него и постепенно приближаясь к нему).

Сканированием можно исследовать функции более чем одного фактора. Так, участок на плоскости (факторное пространство для двух факторов) можно покрыть сетью узлов и таким образом исследовать поведение функции на этом участке. В принципе это возможно в любом n-мерном пространстве, но по мере увеличения n резко растет число необходимых расчетов и падает эффективность метода.

Другие методы поиска более эффективны, но не обладают той универсальностью, которой отличается сканирование. Их эффективность связана с тем, что это методы направленного поиска, в которых не просто исследуется область факторного пространства, а происходит продвижение в этом пространстве в сторону искомого экстремума. Уже описанное выше сканирование с переменным шагом означает направленность поиска: вблизи экстремума прекращается дальнейшее движение вдоль оси х и начинается сгущение точек около экстремума.

43. Метод деления пополам (одномерная оптимизация).

Как и при описании сканирования, будем искать максимум на отрезке [а, b], показанном на рис. 1. Для этого разделим отрезок пополам – на рисунке точка л (левая). Рассчитаем значение F(л) в этой точке. Пока еще ничего нельзя сказать об экстремуме, кроме того, что он принадлежит нашему отрезку.

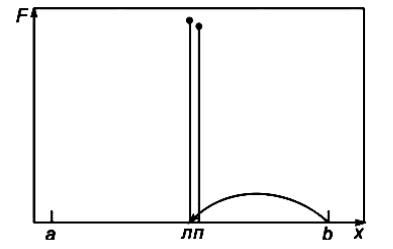
Рис. 1. График поиска максимума методом дихотомии (метод деления пополам).

Выберем малое приращение фактора, равное ε, и поставим на отрезке правую точку п=л +ε. Рассчитаем F(п). Поскольку F(л) > F(п), как изображено на рис. 1, можно утверждать, что если F(x) унимодальна (Что такое унимодальная функция? В допустимой области она имеет только один экстремум нужного знака (один максимум, если ищем максимум, или один минимум в противном случае), то максимум находится в левой половине отрезка.

Теперь отбросим правую половину отрезка (на ней максимума нет). Для этого правый конец (точку b) перенесем в точку л и обозначим ее буквой b (такая операция переименования не вполне привычна для традиционной математики, но в алгоритмических языках она чрезвычайно распространена). На рис. 1 этот перенос показан стрелкой. Разумеется, при F(л) < F(п) в точку л мы перенесли бы точку а. Можно перенести конец отрезка и в точку п, но так как л и п близки, то это почти одно и то же.

После того как правый конец отрезка перенесен, задача вернулась к исходным условиям: задан отрезок от а до b, на котором нужно найти максимум. Поэтому проводится следующий цикл расчета, ничем не отличающийся от предыдущего, кроме значения b. Снова делим пополам отрезок, ставим вспомогательную точку на расстоянии ε, переносим в середину либо правый, либо левый конец. Такой алгоритм (расчет слагается из одинаковых циклов, различающихся лишь начальными условиями) называют итерационным.

В принципе итерации можно проводить до бесконечности: делить пополам все меньшие отрезки. Поэтому в любом итерационном