
- •1. Матрицы и действия над ними.
- •2. Определители второго и третьего порядков.
- •3. Миноры и алгебраические дополнения.
- •4. Обратная матрица.
- •5. Решение систем линейных алгебр. Уравнений. Теорема Крамера.
- •6. Линейная балансовая модель Леонтьева.
- •7. Метод Гаусса-Жордана.
- •8. Ранг матрицы. Теорема Кронекера-Капелли.
- •9. Прямоугольная система координат в пространстве. Понятие вектор. Проекция вектора на ось. Направляющие косинусы вектора.
- •10. Линейные операции над векторами. Теоремы о проекциях векторов. Линейная зависимость векторов.
- •11. Скалярное произведение векторов. Выражение скалярного произведения через координаты векторов.
- •12. Векторное произведение. Выражение векторного произведения через координаты векторов.
- •13. Смешанное произведение трех векторов. Выражение смешанного произведения через координаты векторов.
- •14. Векторное параметрическое уравнение прямой. Задача о делении отрезка в зад. Отношении.
- •1 5. Координатные уравнения прямой в пространстве.
- •16. Координатные уравнения прямой на плоскости.
- •17. Угол между двумя прямыми. Взаимное расположение прямых на плоскости.
- •18. Координатные уравнения плоскости.
- •19. Общие уравнения прямой в пространстве.
- •2 0. Взаимное расположение прямых и плоскостей в пространстве
- •22. Поверхность второго порядка
- •1. Множества. Грани числовых множеств. Абсолютная величина числа. Понятие функции. Классификация функций.
- •2.Предел последовательности. Понятие сходящейся последовательности. Теоремы о сходящихся последовательностях (единственный предел, необходимое условие сходимости)
- •4.Первый замечательный предел.
- •5.Второй замечательный предел.
- •6.Бесконечно-большие и бесконечно‑ малые функции. Сравнение бесконечно‑малых функций. Асимптотические формулы.
- •7.Непрерывность функции в точке. Классификация точек разрыва.
- •8.Основные теоремы о непрерывных функциях.
- •9.Понятия сложной и обратной функций.
- •10. Понятие производной. Геометрический и физический смыслы производной.
- •11. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности.
- •12. Правила дифференцирования суммы, разности, произведения и частного.
- •13. Понятие дифференциала. Дифференциал суммы, разности, произведения и частного.
- •14. Производные постоянной, тригонометрических и логарифмической функций.
- •15. Производные обратной и сложной функций
- •16. Производные показательной и обратных тригонометрических функций.
- •17. Логарифмическая производная. Производная степенной функции.
- •18. Таблица производных простейших элементарных функций.
- •19. Дифференцирование функции, заданной параметрически.
- •20. Теоремы Ферма и Ролля.
- •21. Теорема Лагранжа и Коши.
- •22. Теорема Лопиталя.
- •23. Теорема Тейлора.
- •24. Признак монотонности.
- •25. Направление выпуклости.
- •26. Необходимые условия точки перегиба.
- •27. Асимптоты графика функции.
- •28. Комплексные числа.
- •29. Тригонометрическая форма комплексного числа.
- •30. Возведение комплексного числа в степень и извлечение корня.
26. Необходимые условия точки перегиба.
Если функция y=f(x) имеет в точке перегиб и непрерывную производную в некоторой окрестности этой точки, то вторая производная в этой точке равна 0. Доказательство: производится от обратного предположения, что вторая производная не равна 0. По теореме о сохранение знака сущ. окрестность, в которой функция имеет тот же знак, что и в точке , а это противоречит условию теоремы. Достаточное условие точки перегиба: для того чтобы имела в точке перегиб, достаточно, чтобы она имела f´´ и разные направления выпуклости слева и справа от этой точки.
27. Асимптоты графика функции.
Асимптоты-
прямая, к которой график функции сколь
угодно раз близко приближается при х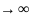 или
в окрестности точек разрыва. Асимптоты
бывают: вертикальными, горизонтальными,
наклонными. Горизонтальная асимптота:
прямая у=
или
в окрестности точек разрыва. Асимптоты
бывают: вертикальными, горизонтальными,
наклонными. Горизонтальная асимптота:
прямая у=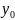 графика f(х)
если
графика f(х)
если
 .
Прямая х=
называется вертикальной асимптотой
графика у=f(х),
если хотя бы один из односторонних
пределов
.
Прямая х=
называется вертикальной асимптотой
графика у=f(х),
если хотя бы один из односторонних
пределов
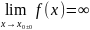 .
у=
.
у=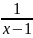 ;
;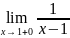 =+
;
=+
;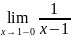 =-
.
у=
=-
.
у= ;
;
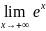 =
=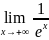 =0, у=0-
горизонтальная асимптота.
=0, у=0-
горизонтальная асимптота.
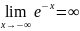 .
Наклонная асимптота- это прямая у=kx+b
график функции у=f(x)
при f(x)=kx+b+
.
Наклонная асимптота- это прямая у=kx+b
график функции у=f(x)
при f(x)=kx+b+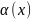 ,
x
,
где
,
x
,
где
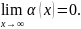 k=
k=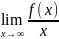 ;
b=
;
b=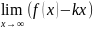 .
Если хотя бы один из пределов не
существует или бесконечен, то наклонной
асимптоты нет. Пример:
y=
.
Если хотя бы один из пределов не
существует или бесконечен, то наклонной
асимптоты нет. Пример:
y=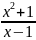 ;
k=
;
k=
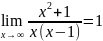 ;
у=
;
у=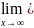 =
=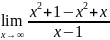 =
= =1
=1
y=1*x+1=x+1
Cхема
исследования графика функции. 1)Область
определения, область значения, чётность,
не чётность, периодичность.2)Характерные
точки графика функции(пересечение с
осями)- х=0,у=0. 3)Точки
возможного экстремума. f´(x)=0
. Интервалы монотонности f´(x)
,
f´(x)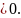 4)Точки
перегиба:f´´(x)=.0
Направление выпуклости f´´(x)
;
f´´(x)˂0.
5)Асимптоты
графика функции 6)
Построение графика на основании
исследования.
4)Точки
перегиба:f´´(x)=.0
Направление выпуклости f´´(x)
;
f´´(x)˂0.
5)Асимптоты
графика функции 6)
Построение графика на основании
исследования.
28. Комплексные числа.
-
это упорядоченная пара действительных
чисел.
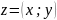 Комплексные числа- это расширенное
понятие числа. z=(x;0)-
действительное число, где х- действенная
часть; у-мнимая часть. z=(0;у)- чисто мнимое
число; z=(0;1)-
мнимая единица-i;
Комплексные числа- это расширенное
понятие числа. z=(x;0)-
действительное число, где х- действенная
часть; у-мнимая часть. z=(0;у)- чисто мнимое
число; z=(0;1)-
мнимая единица-i;
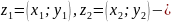 равные
числа
=
;
равные
числа
=
;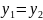 Действие
над комплексными числами Суммой(разностью)
2-х комплексных чисел называется число,
определяемое следующим образом: z=
Действие
над комплексными числами Суммой(разностью)
2-х комплексных чисел называется число,
определяемое следующим образом: z=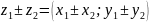 Комплексное
число может быть представлено в виде:
z=x+iy(алгебраическая
форма)=(
Комплексное
число может быть представлено в виде:
z=x+iy(алгебраическая
форма)=(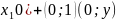
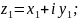
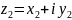 z=
z=
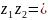 +i
+i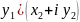 =
(
=
(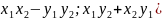
 )
)
29. Тригонометрическая форма комплексного числа.



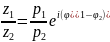

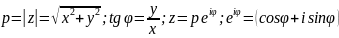 φ=Arg
Z=2
φ=Arg
Z=2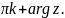 0
0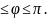
z=1,
x=1; y=0; p=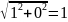
cos
=1;
tg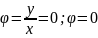
z=1(cos 0+ i sin 0)= cos 0+ i sin 0 = 1+i
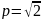 ;
tg
;
tg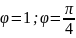
z=1+i=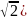 )
)
30. Возведение комплексного числа в степень и извлечение корня.
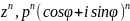
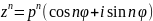
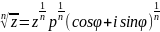
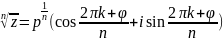
k=0,1,2,..,n-1
Формулы Эйлера:
Формула
Эйлера утверждает, что для
любого действительного и
комплексного числа x выполнено
следующее равенство: eix
= cosx
+ sinx,
где е — одна
из важнейших математических констант,
определяющаяся следующей формулой: 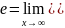 ,
i — мнимая
единица.
,
i — мнимая
единица.
Доказательство формулы Эйлера можно провести с использованием рядов Тейлора. Разложим функцию eix в ряд Тейлора в окрестности точки a = 0 по степеням x. Получим:
![]()
Но
![]()
![]()
Поэтому eix = cosx + sinx ч. т. д.
1. Матрицы и действия над ними. 1
6. Линейная балансовая модель Леонтьева. 1
7. Метод Гаусса-Жордана. 1
8. Ранг матрицы. Теорема Кронекера-Капелли. 2
9. Прямоугольная система координат в пространстве. Понятие вектор. Проекция вектора на ось. Направляющие косинусы вектора. 2
10. Линейные операции над векторами. Теоремы о проекциях векторов. Линейная зависимость векторов. 3
11. Скалярное произведение векторов. Выражение скалярного произведения через координаты векторов. 3
12. Векторное произведение. Выражение векторного произведения через координаты векторов. 3
13. Смешанное произведение трех векторов. Выражение смешанного произведения через координаты векторов. 3
14. Векторное параметрическое уравнение прямой. Задача о делении отрезка в зад. отношении. 3
15. Координатные уравнения прямой в пространстве. 3
16. Координатные уравнения прямой на плоскости. 3
17. Угол между двумя прямыми. Взаимное расположение прямых на плоскости. 3
18. Координатные уравнения плоскости. 4
19. Общие уравнения прямой в пространстве. 5
20. Взаимное расположение прямых и плоскостей в пространстве 5
22. Поверхность второго порядка 5
1. Множества. Грани числовых множеств. Абсолютная величина числа. Понятие функции. Классификация функций. 7
2.Предел последовательности. Понятие сходящейся последовательности. Теоремы о сходящихся последовательностях (единственный предел, необходимое условие сходимости) 7
3.Бесконечно-большие и бесконечно-малые последовательности. Теоремы о сумме (разности), произведении и частном двух сходящихся последовательностях. Предельный переход в неравенствах. Монотонные последовательности. Число ℮. Предел функции. Теоремы о пределах функции. 7
4.Первый замечательный предел. 8
5.Второй замечательный предел. 9
6.Бесконечно-большие и бесконечно‑ малые функции. Сравнение бесконечно‑малых функций. Асимптотические формулы. 9
7.Непрерывность функции в точке. Классификация точек разрыва. 9
8.Основные теоремы о непрерывных функциях. 9
9.Понятия сложной и обратной функций. 9
11. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности. 10
12. Правила дифференцирования суммы, разности, произведения и частного. 10
13. Понятие дифференциала. Дифференциал суммы, разности, произведения и частного. 10
14. Производные постоянной, тригонометрических и логарифмической функций. 11
15. Производные обратной и сложной функций 11
16. Производные показательной и обратных тригонометрических функций. 11
18. Таблица производных простейших элементарных функций. 11
19. Дифференцирование функции, заданной параметрически. 12
20. Теоремы Ферма и Ролля. 12
21. Теорема Лагранжа и Коши. 12
23. Теорема Тейлора. 13
24. Признак монотонности. 13
25. Направление выпуклости. 13
26. Необходимые условия точки перегиба. 13
27. Асимптоты графика функции. 13
28. Комплексные числа. 13
29. Тригонометрическая форма комплексного числа. 13
30. Возведение комплексного числа в степень и извлечение корня. 14
-
sin2x+cos2x=1
tg2x+1=
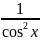
ctg2x+1=
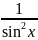
tgx=
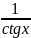
tgx*ctgx=1
tgx=
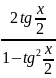
sinx=
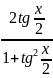
cosx=
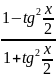

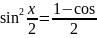
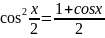
cos(-α)=cos α
sin(-α)=-sin α
tg(-α)=-tg α
ctg(-α)=-ctg α
sin2x=2 sinx cosx
sin3x=2sinx-4sin3x
sin4x=2sin2x–cos2x
cos2x=cos2x-sin2x cos2x=2cos2x-1
cos2x=1-2sin2x
cos3x=4cos3x-3cosx
tg2x=
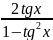
tg3x=
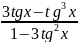
cos(π/2-x)=sin x
cos(π±x)=-cos x
cos(π/2+x)=-sin x
cos(3π/2-x)=-sin x
cos(3π/2+x)=sin x
sin(π/2±x)=cos x
sin(π-x)=sin x
sin(π+x)=-sin x
sin(3π/2±x)=-cos x
tg(π/2+x)=-ctg x
tg(π/2-x)=ctg x
ctg(π/2+x)=-tg x
ctg(π/2-x)=tg x
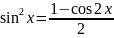

)0)))
sin(x+y)=sinx·cosy+cosx·siny
sin(x-y)=sinx·cosy-cosx·siny
cos(x+y)=cosx·cosy–sinx·siny
cos(x-y)=cosx·cosy+sinx·siny
tg(x+y)=
 tg(x-y)=
tg(x-y)=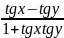
sinx+siny=2 sin(
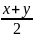 )·cos(
)·cos(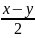 )
)sinx-siny=2 sin( )·cos( )
cosx+cosy=2 sin( )·sin( )
cosx+cosy=-2 sin( )·sin( )
|
0 |
30 |
45 |
60 |
90 |
120 |
135 |
150 |
180 |
210 |
225 |
240 |
270 |
300 |
315 |
330 |
360 |
||
sin |
0 |
|
|
|
1 |
|
|
|
0 |
|
|
|
-1 |
|
|
|
0 |
||
cos |
1 |
|
|
|
0 |
|
|
|
-1 |
|
|
|
0 |
|
|
|
1 |
||
tg |
0 |
|
1 |
|
- |
- |
-1 |
|
0 |
|
1 |
|
- |
|
-1 |
|
0 |
||
ctg |
- |
|
1 |
|
0 |
|
-1 |
- |
- |
|
1 |
|
0 |
|
-1 |
|
- |
||
arc |
0 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
2π |
||
х2 - у2 = (х - у) (х+у) (х + у)2 = х2 + 2ху + у2 (х - у)2 = х2 – 2ху + у2 (х + у)3 = х3 + 3х2у + 3ху2 + у3 (х - у)3 = х3 – 3х2у + 3ху2 - у3 х3 + у3 = (х + у) (х2 - ху + у2) х3 - у3 = (х - у) (х2 + ху + у2) |
alogab = b loga 1 = 0 loga a = 1 |
logax= logax= |
|||||||||||||||||
loga(x · y) = logax + logay loga xy = logax - logay loga xp = p logax logak x = |
|||||||||||||||||||
(f(x)+g(x))’=f ’(x)+g’(x) (k•(f(x))’ = k•f ’(x) (f(x)•g(x))’=f ’(x)·g(x)+f(x)·g’(x) (f(x)/g(x))’= (f(g(x))’=f ‘(g(x))•g’(x) lim
f(x)g(x)= lim ex = ∞, x→+∞; 0, x→-∞ |
при
arccsin x ̴x tg x ̴x arctg x ̴x 1-cos x ̴ x2/2 |
ax ̴1+x lna ex-1 ̴x ln (1+x) ̴x loga(1+x) ̴x/lna (1+x)m-1 ̴mx |
|||||||||||||||||
lim(1+x)1/x=e |
|||||||||||||||||||

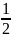

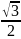
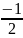


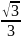

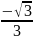


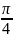


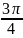

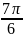
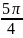
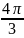

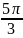
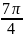
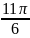
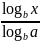

 loga x,
при k ≠
0
loga x,
при k ≠
0
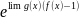
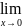 sin
x
̴x
sin
x
̴x