Поскольку , то из можно записать:

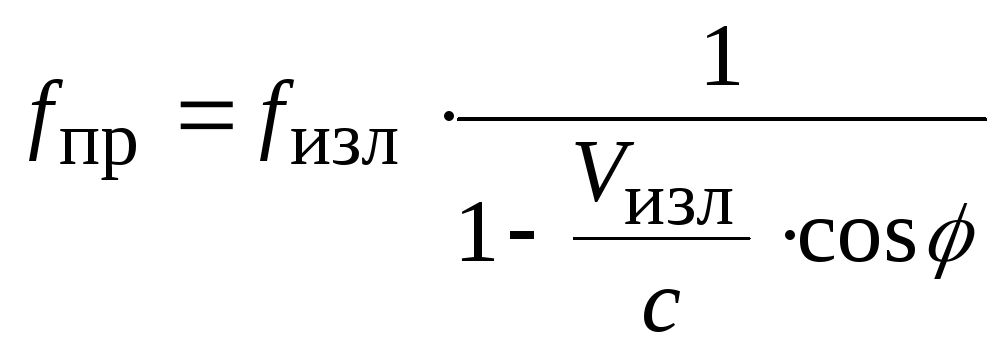, или . (3.62)

Домножим правую часть (3.62) на знаменатель с обратным знаком и, тогда:

.

Т.к., обычно , когда скорость движения излучателя значительно меньше скорости звука в среде, то приближенно:

. (3.63)

Эффект Доплера в рассмотренном случае физически обусловлен “деформацией” акустического поля за счет движения источника.

42. Эффект Доплера. Неподвижный излучатель, подвижный преемник.

Эффект Доплера заключается в том, что в результате взаимного перемещения источника и приемника звука относительно неподвижной акустической среды, частота сигнала, фиксируемая приемником, отличается от частоты сигнала, излученного источником.

Источник неподвижен, приемник перемещается

В отличие от предыдущего случая, т.к. при движении приемника никакой деформации излучаемого поля не происходит, то приемник просто с большей частотой встречается с волновыми фронтами (см. рис. 3.14).

Рис. 3.14

Формула для определения частоты принимаемого сигнала равенство является строгим:

. (3.64)

Поэтому при q = 0 и  с, частота принимаемого сигнала стремится к удвоенному значению по сравнению с частотой излучаемого сигнала.

43. Эффект Доплера. Подвижный излучатель и приемник.

Эффект Доплера заключается в том, что в результате взаимного перемещения источника и приемника звука относительно неподвижной акустической среды, частота сигнала, фиксируемая приемником, отличается от частоты сигнала, излученного источником.

Источник и приемник подвижны.

В этом случае сигналы, поступающие от обоих объектов, перемножаются и для частоты приема можно на основании результатов, полученных для двух предшествующих вариантов, записать точное соотношение:

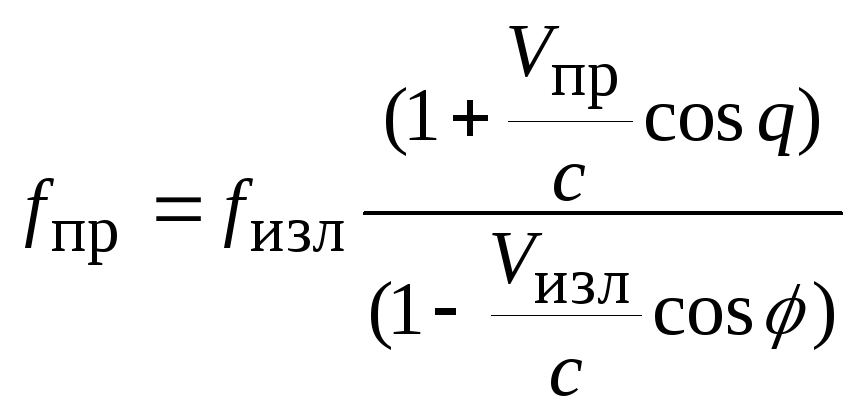. (3.65)

Рис. 3.15

Очевидно, что при малости скорости движения излучателя по сравнению со скоростью звука:, тогда (3.65) превратится в:

^.

Раскрываем скобки и, учитывая , получим:

. (3.66)

Таким образом, отклонение частоты носит знакопеременный характер. Его величина определяется формулой:

. (3.67)

Максимальное отклонение частоты по (3.67) при φ=0, q = 180º и φ=180º, q = 0 составит:

.

44. Эффект Доплера в режиме эхо-локации.

Эффект Доплера заключается в том, что в результате взаимного перемещения источника и приемника звука относительно неподвижной акустической среды, частота сигнала, фиксируемая приемником, отличается от частоты сигнала, излученного источником.

Эхолокация ( И + П – совмещены на подвижном носителе , цель – осуществляет перемещение).

При приеме эхо-сигнала изменение частоты из-за эффекта Доплера будет выражено более сильно, чем при прямом обмене. Причина этого в том, что падение акустической волны на препятствие и отражение от него можно отождествить с излучением и приемом «вторичных» волн.

Тогда точным выражением для изменения частоты сигнала будет:

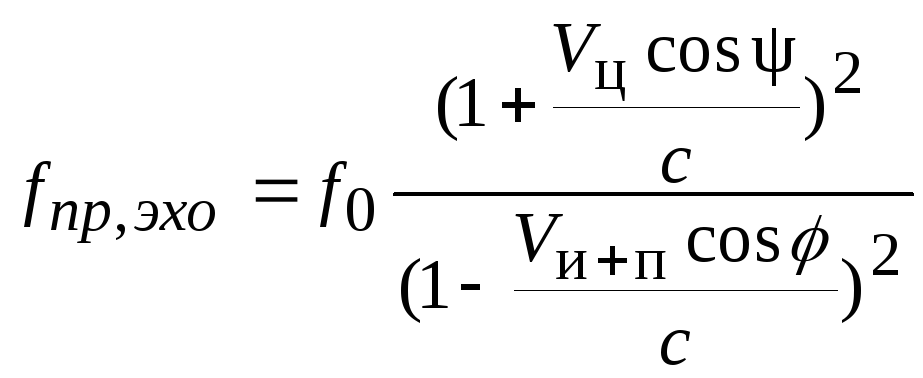. (3.68)

с учетом :

. (3.69)

Тогда, с учетом максимальное отклонение частоты:

. (3.70)

45. Рассеяние звука на шероховатой поверхности.

Достаточно часто приходиться встречаться с отражением упругих волн от поверхностей, отличающихся различной степенью неровности .

При отражении звука от шероховатых поверхностей наряду с зеркально отраженной волной возникают и компоненты рассеяния в других направлениях, определяемых соотношениями длины волны и параметров поверхностей.

1.Средняя высота (амплитуда) шероховатостей много меньше длины волны звука (диффузное рассеяние);

2. Протяженность неровностей вдоль поверхности и их радиуса должно быть много больше длины волны звука ().

Количественный критерий для описания условий рассеяния определяется параметром Рэлея: , где- волновое число,- средняя высота неровностей, - угол падения плоской волны. Для диффузного рассеяния  1.

Волновой процесс в окрестности периодически шероховатой (волнистой) поверхности в плоскости xoz:

, (3.43)

Решение для произвольного приближения имеет вид: (при этом временной множитель учитывать не будем):

, (3.45)

где .

при , кроме зеркально отраженной волныобразуется система дифракционных «пучков» - угловых спектров с амплитудами, спадающими по закону. При учете энергии, уносимой только волной «нулевого спектра», коэффициент отражения от неровной поверхности определяется выражением. Именно образование «дифракционных» пучков-спектров и является причиной диффузного рассеяния. Один из этих «спектров» может совпасть с падающей волной, образуяобратно отраженную волну.

46. Интеграл Кирхгофа.

Требуется найти связь между значением в некоторой области пространстваV для точки наблюдения (.) М и значением Ф на поверхности S. Такая связь может быть получена путем использования формулы Грина.

Формула Грина:

.

n – внешняя нормаль. внутри объема V существует два звуковых поля, описываемых функциями и, которые удовлетворяют уравнению Гельмгольца:

.

Звуковое поле – это основное поле, которое требуется определить; полеявляется вспомогательной величиной. Звуковое полев уравнении Гельмгольца (3. ) умножим на, а второе уравнение - на, затем вычтем второе уравнение из первого и сумму проинтегрируем по объемуV.

.

Применяя к последнему выражению формулу Грина, можно записать:

.

Выберем в качестве поле точечного ненаправленного источника, помещенного в точке наблюдения М.

(3.50)

где ,- радиус вектор, проведенный от начала координат в точку наблюдения М;- радиус вектор, направленный в любую точку поля.

В сферической системе координат в силу симметрии задачи уравнение Гельмгольца можно записать в виде:

. (3.51)

Прямой подстановкой легко установить, что функция удовлетворит этому уравнению.

Окружим точку М малой сферой радиусаа. Новая область будет расположена между и, аполная новая поверхность, ограничивающая объем, будет состоять из двух частей и.

Рассмотрим интеграл по поверхности . Наружная к области нормаль к поверхностибудет направлена внутрь сферы. Из-за этого наимеем. Сколь бы малым ни выбиралось значение радиуса окружности - а, величины ина поверхности будут оставаться конечными, так что применение формулы Грина является допустимым.

Вычислим:

. (3.52)

Поскольку искомое поле является непрерывной функцией координат в любой точке области, то в пределах малой сферы радиуса а, можно считать, что имало зависит от положения точки на поверхности. Поэтомуиможно вынести из под знака интеграла, заменив их значения в точке, определенной вектором. Для функцииэтого сделать нельзя, так как внутриона обладает особенностью.

В результате можно записать:

.

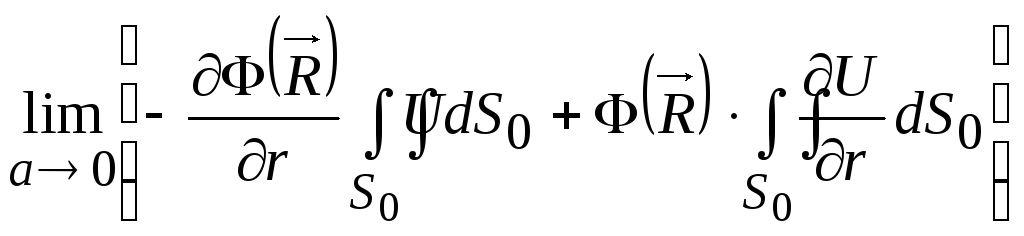Учитывая, что на поверхности :

,

где – элемент телесного угла, получим:

.

Отметим, что поверхность интегрирования является суммой S и . Тогда получим, что, откуда:

. (3.53)

Так как интегрирование проводится по поверхности , то величиныв этой формуле являются расстоянием от точки наблюденияМ до элемента поверхностиS.

Полученное выражение носит название формулы Кирхгофа или интеграла Кирхгофа.

47. Интегральные формулы Гюйгенса.

.

Полученное выражение носит название формулы Кирхгофа или интеграла Кирхгофа.

Запишем формулу интеграла Кирхгофа в виде.

. (3.54)

где U – вспомогательная функция, представляющая собой поле точечного источника. Выберем в качестве U функцию, которая описывает поле точечного источника, расположенного над абсолютно жесткой поверхностью. в точке М поле от источника, помещенного в произвольную точку над плоскостью может быть представлено в виде суммы полей источника и зеркально расположенного источника:

.

Нормальная производная этого поля определяется выражением:

.

Устремим точку Q к границе. Учитывая, что на границе ,, получим. Подставляя эти значения в формулу ,получим:

.

Выражение называется первой интегральной формулой Гюйгенса. здесь для расчета звукового поля во всем полупространстве требуется знать только одну величину , т.е. колебательную скорость поверхности. Перейдем от потенциалов к колебательной скорости и звуковому давлению:;. Тогда:

Полученное выражение служит основной формулой для расчета звуковых полей плоских излучателей и приемников звука. Для того, чтобы получить вторую интегральную формулу Гюйгенса, следует в качестве вспомогательной функции выбрать поле точечного, ненаправленного источника, расположенного над абсолютно мягкой поверхностью. В этом случае поле мнимого источника будет противоположно по знаку полю источника:

.

Вычислив производную и устремив точкуQ к границе, получаем: . Тогда:

.

Это выражение и есть вторая интегральная формула Гюйгенса, определяющая значения звукового давления в полупространстве по известной величине звукового давления на плоскости.