§9 Локальные экстремумы фнп. Необходимый признак л.Э.

Пусть функция f непрерывна в точке и, следовательно, определена в некоторой окрестности точки. Сравним значения f(a) и f(ПО(а,r)).

Определение.

Точка а называется точкой локального экстремума (л.э.)непрерывной функции f, если .

Следствия.

1. Точка л.э. ФНП f является точкой л.э каждой из n функций одной переменной , которые являются «сужениями f» на прямые, параллельные соответствующим координатным осям. Известно, что ФОП достигает л.э лишь в критических точках

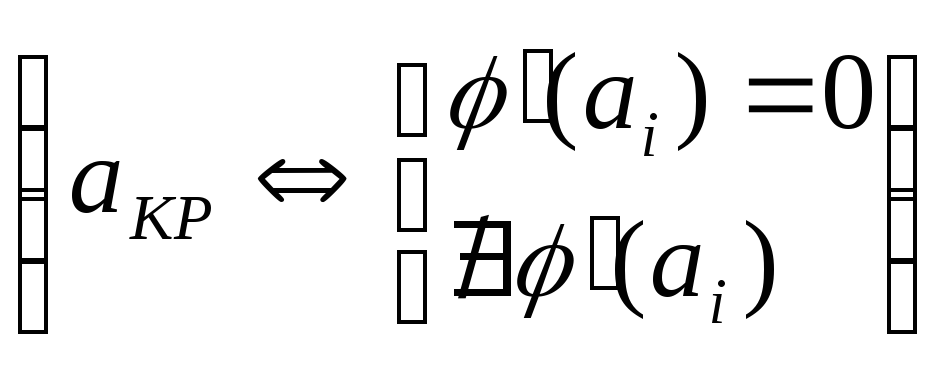.Поэтому

2) Необходимый (но не достаточный !) признак Л.Э. ФНП. Дифференцируемая ФНП достигает л.э. лишь в критических точках

Замечания.

1) Признак является необходимым, но не является достаточным признаком локального экстремума: не всякая «критическая точка» непрерывной функции является точкой локального экстремума. 2) Для функции двух переменных касательная плоскость к поверхности z=f(x,y) в точке Л.Э. либо параллельна координатной плоскости XOY (), либо не существует.

Пример-1. Функция непрерывна , , имеет единственную «критическую» точку а(0,0), которая является точкой локального минимума, т.к. (

Пример-2. Точка а(0,0) является стационарной точкой функции . f достигает в ней л. максимума f_max=f(0,0)=1, так как

§10. Достаточное условие локального экстремума фнп.

Воспоминание из Линейной Алгебры.

Квадратичная форма двух переменных имеет «канонический вид» в прямоугольной системе координат , определяемой собственными векторами матрицы квадратичной формы

Пусть точка – стационарная точка функции .

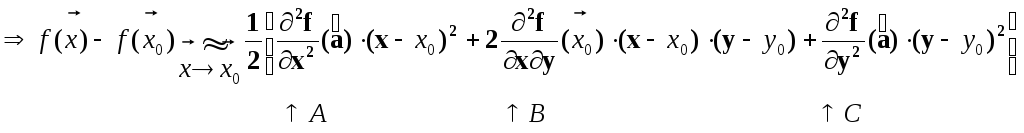Обозначим б/м приращения аргументов:

Таким образом, «приращение» функции в окрестности стационарной точки определяется квадратичной формой, матрица которой – симметричная матрица Гессе

Из линейной алгебры известно, что квадратичная форма имеет канонический вид

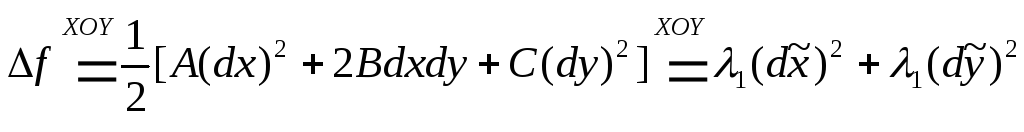(1)

причем собственные числа матрицы G(x₀) вещественны и являются решениями уравнения

(2)

причем по теореме Виета: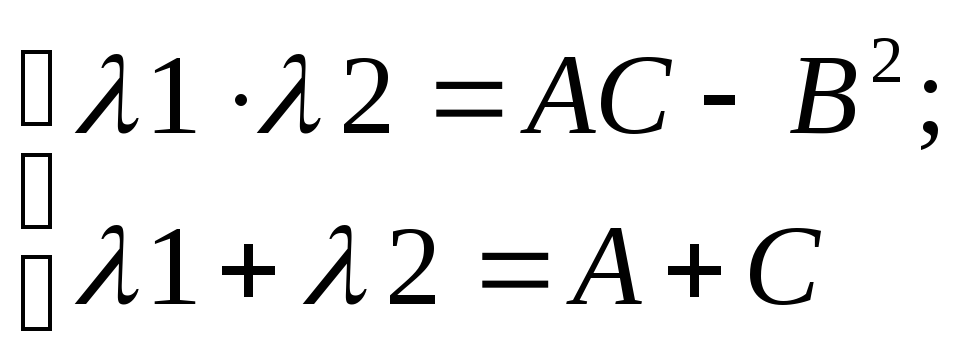

Из (1) и определения локального экстремума функции 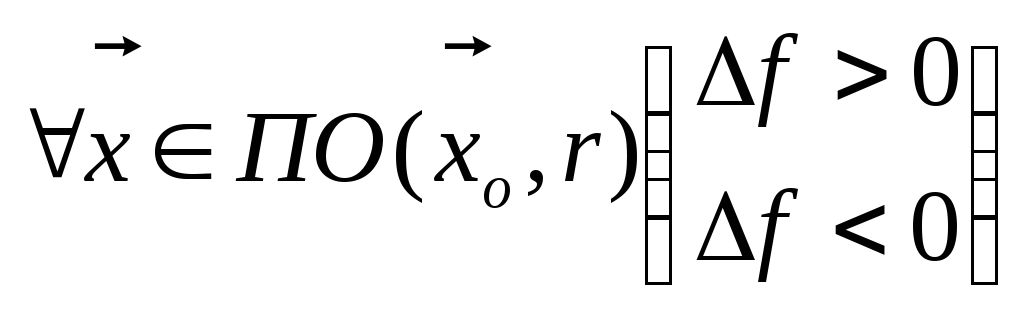следует

Утверждения.

1) Достаточный признак локального экстремума ФНП

Дважды непрерывно дифференцируемая в стационарной точке функция f достигает в этой точке локального экстремума, если собственные числа матрицы Гессе положительны (или отрицательны (.

2) Если собственные числа матрицы Гессе не одного знака (λ₁∙ λ₂<0), стационарная точка не является точкой Л.Э.

3) Если хотя бы одно из собственных чисел матрицы Гессе равно нулю, формула Тейлора 2 порядка недостаточна для анализа стационарной точки.

4) Можно показать (экз.+1), что из соотношения (1) и теоремы Виета вытекает следующее правило анализа стационарной точки функции двух переменных:

4.1)  стационарная точка является точкой локального минимума.

3.2)  стационарная точка является точкой локального максимума.

3.3) D<0  стационарная точка не является точкой локального экстремума функции.

3.4) D=0  формула Тейлора 2 порядка не достаточна для анализа стационарной точки.

==========================

Пример-1. Найти и исследовать стационарные точки функции f(x,y)=xy+x²+y³

1)f’(x,y)=[y+2x;x+3y²]=[0;0] {(0;0);(-1/12; 1/6)}

2)

G(-1/12;1/6)=

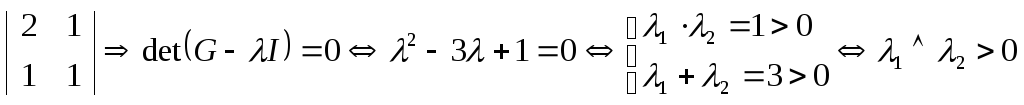
 ст. точка (-1/12;1/6)- точка локального минимума: f_min=f(-1/12;1/6)= - 2.315∙10^-3.

ЭКЗ.: Исследовать Л.Э. функции