§10.3. Погрешность интерполяции.

ОПРЕДЕЛЕНИЕ. Величина называется остаточным членом интерполяции.

Справедлива следующая теорема.

ТЕОРЕМА10.2.(без док-ва). Пусть функция дифференцируема (n+1) раз на отрезке [a,b], содержащем узлы интерполяции . Тогда для погрешности интерполяции в точке справедлива оценка:

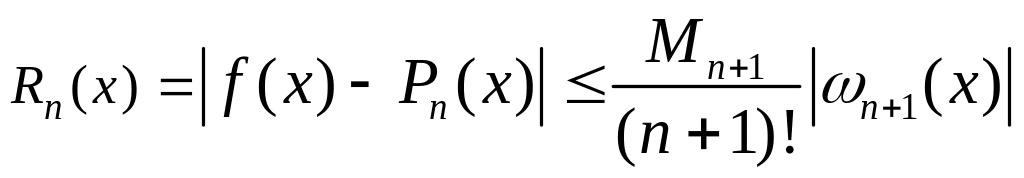(10.6)

Где ,

ПРИМЕР 10.4. Оценим величину погрешности для выше рассмотренного примера.

, ,

Ясно, что .Тогда

Наряду с интерполированием применяют и экстраполирование, то есть вычисление значений функции вне отрезка интерполяции. При этом величина погрешности экстраполяции существенно выше, чем интерполяции. Это связано с поведением функции

Например,

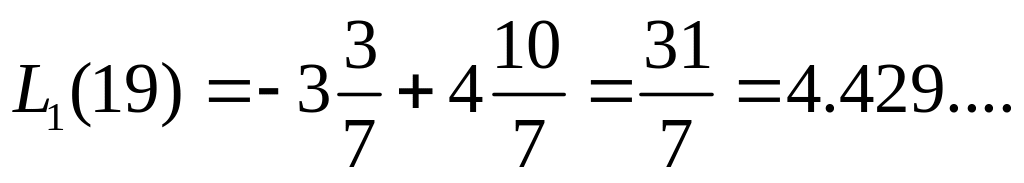, погрешность равна 0.07.

Для оценки погрешности можно использовать более простую оценку, в случае, если шаг таблицы постоянный:

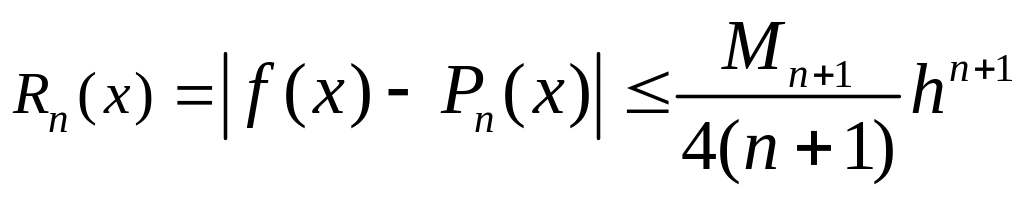(10.7)

§10.4. Многочлен ньютона с конечными разностями.

Пусть функция задана на множестве дискретных точек , , … значений аргумента с постоянным шагом .

ОПРЕДЕЛЕНИЕ. Конечной разностью 1-го порядка называется величина

(10.8)

ОПРЕДЕЛЕНИЕ. Конечной разностью -го порядка называется величина

(10.9)

Таблицу конечных разностей обычно располагают следующим образом:

ДИАГОНАЛЬНАЯ ТАБЛИЦА КОНЕЧНЫХ РАЗНОСТЕЙ

Можно показать, что конечные разности порядка k выражаются через значения функции в (k+1) точке по формулам:

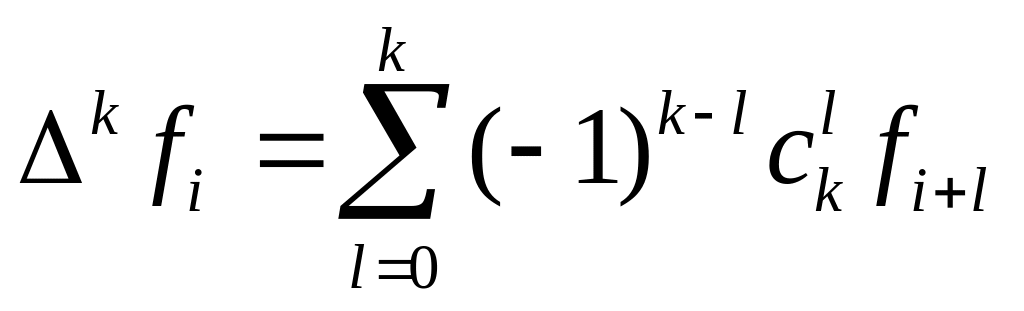, где 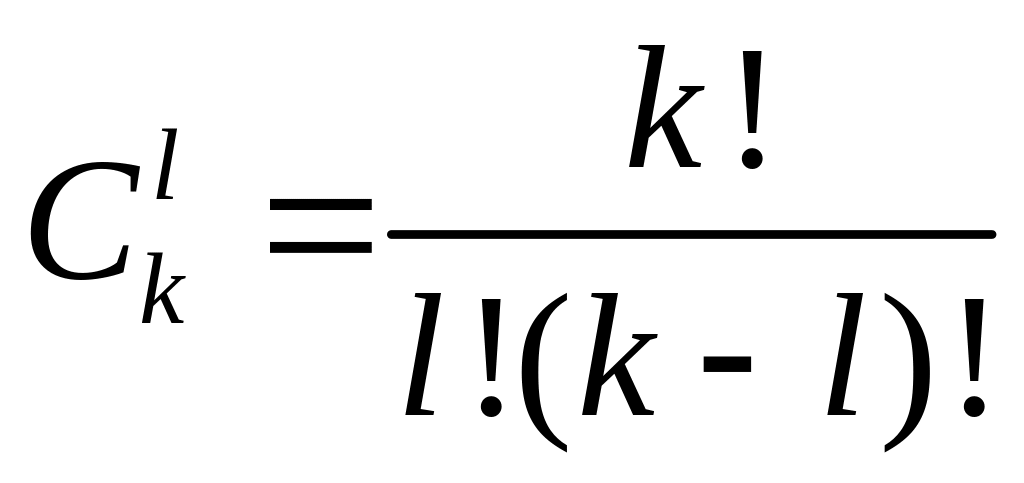- биномиальные коэффициенты.

Найдем 2-ую конечную разность:

3-ья конечная разность , выраженная через значения функции примет вид:

Будем искать интерполяционный многочлен в виде следующего многочлена:

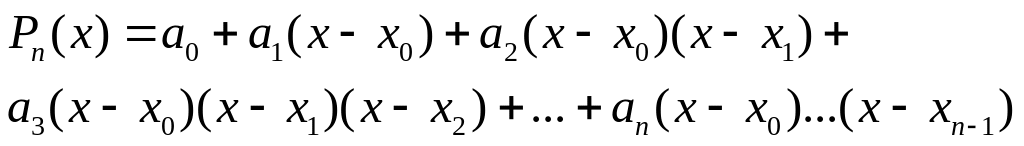
Коэффициенты многочлена будем находить из условия интерполяции:

,

,

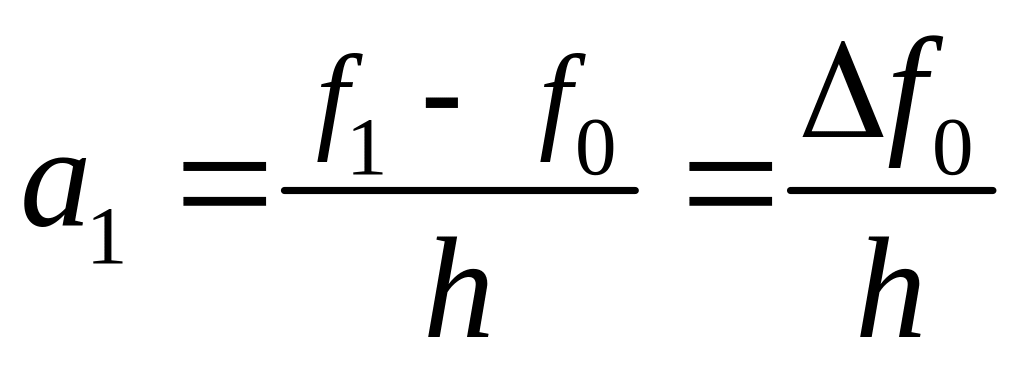
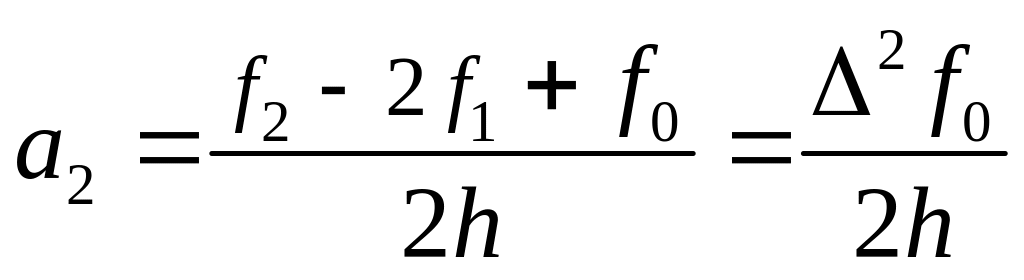
И т.д. Окончательно, многочлен примет следующий вид:

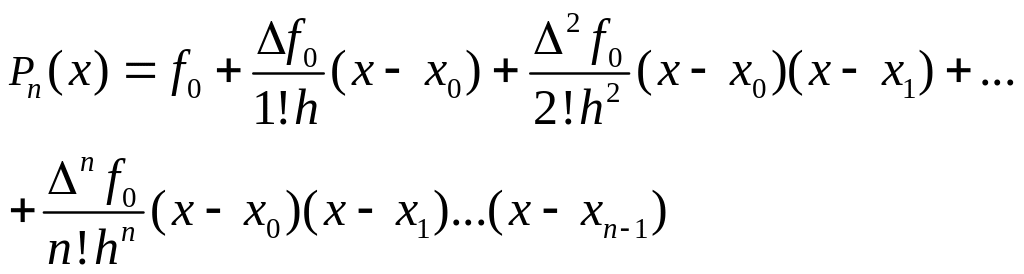(10.10)

Многочлен (10.10) называется многочленом Ньютона с конечными разностями при интерполировании вперед.

ПРИМЕР10.5.

x	0.5	1	1.5	2
f(x)	9/2	3	4/3	3

Составим диагональную таблицу конечных разностей. Очевидно, что шаг таблицы h=0.5.

0.5	9/2
		3-9/2= -3/2
1	3		-5/3+3/2=-1/6
		4/3-3= -5/3		10/3+1/6=21/6=7/2
1.5	4/3		5/3+5/3=10/3
		3-4/3=5/3
2	3

Составим интерполяционный многочлен Ньютона с конечными разностями.

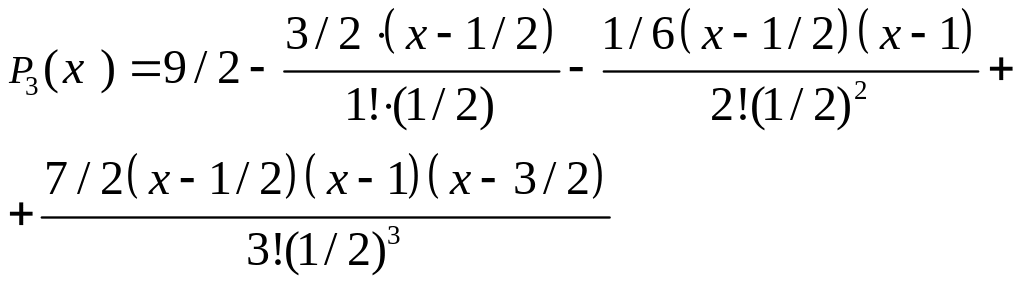
Преобразуем многочлен, чтобы получить каноническую форму.

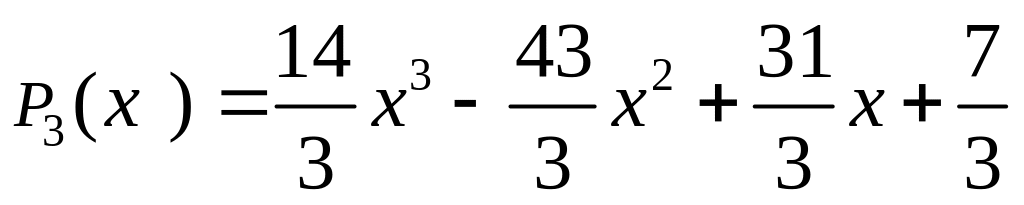
Легко проверить, что в узлах таблицы многочлен совпадает со значениями функции.

Интерполирование можно производить от любой точки вперед и назад.

Например, при интерполирование назад интерполирование производится снизу-вверх:

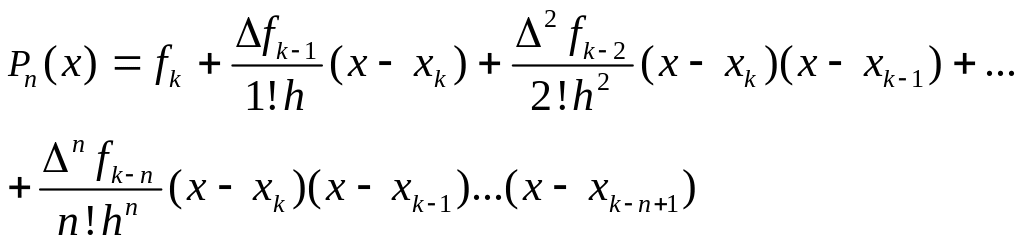
Для предыдущего примера:

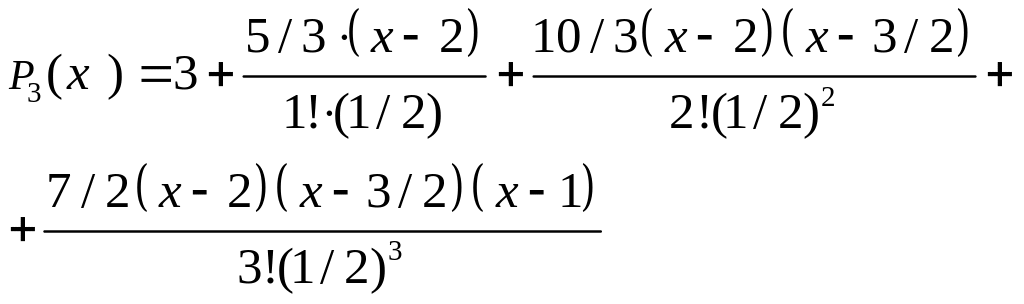
Утверждение. Пусть функция f дифференцируема k раз на отрезке .

Тогда

, где

Так как справедливо утверждение о том, что , то

Можно вычислить величину .

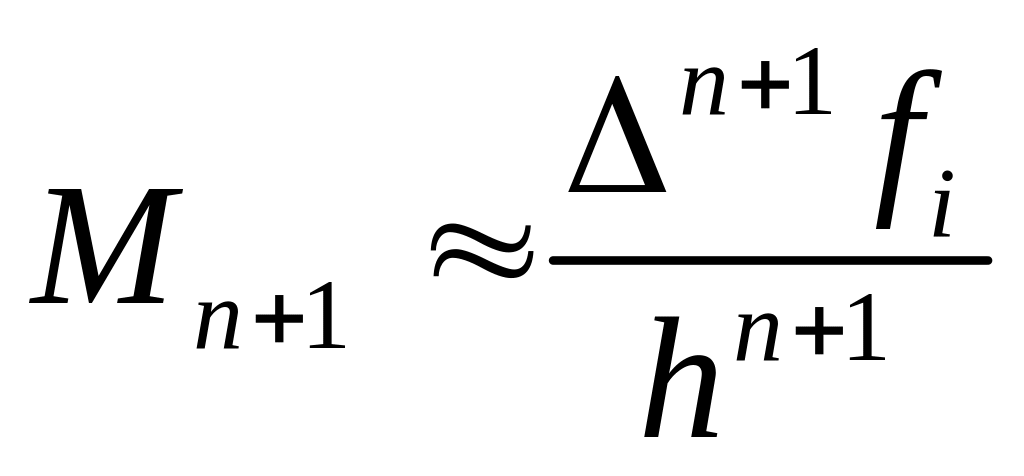[2] К.О. Казенкин. Приближение функций. Численное интегрирование. Численное дифференцирование.МЭИ. 2012.