§11.3. Кусочно-полиномиальная интерполяция.

Пусть функция интерполируется на отрезке [a,b].

Определение. Метод решения задачи интерполяции единым для всего отрезка многочленом называют глобальной полиномиальной интерполяцией.

Казалось бы хорошо иметь один многочлен, пригодный для приближения функции f во всех точках отрезка [a,b]. Однако существуют весьма веские причины, по которым глобальная интерполяция многочленами высокой степени, как правило, не используется.

1.Отсутствие сходимости при увеличении числа узлов.

Для того, чтобы реализовать процесс интерполяции функции многочленами все возрастающей степени n необходимо указать стратегию выбора при каждом n набора узлов.

n=0

n=1

n=2

……

Рассмотрим простейшую стратегию, состоящую в равномерном распределении узлов на отрезке [a,b] , то есть будем выбирать узлы интерполяции так:

(i=0,1,…n), где .

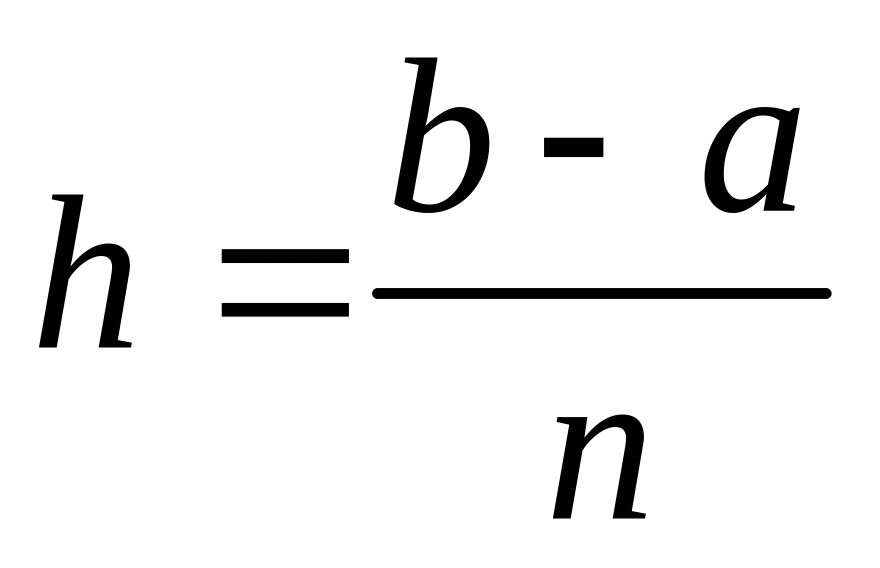Существует классический пример, показывающий, что такая стратегия не обеспечивает сходимости даже для бесконечно дифференцируемой функции.

ПРИМЕР 11.3 (функция Рунге). Будем приближать интерполяционным многочленом

на отрезке [-1,1] функцию 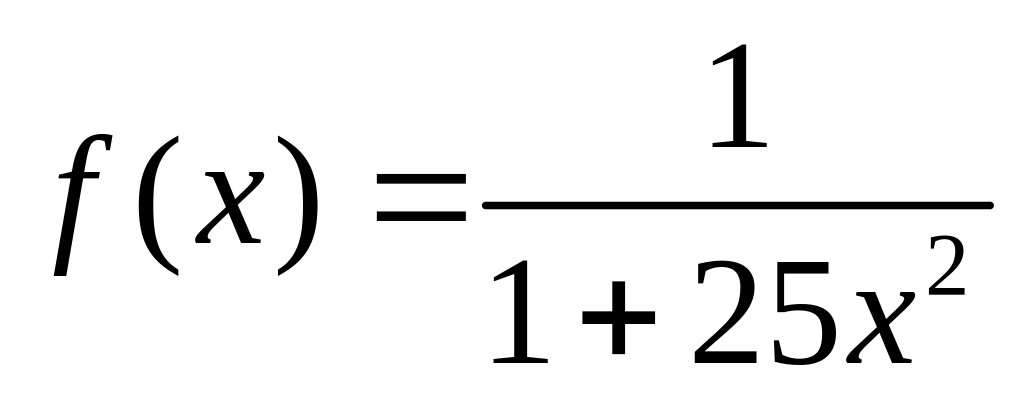. Вычисления показывают, что в центральной части отрезка интерполяция при больших n дает отличные результаты, в то же время при для значений x: наблюдается полиномиальное раскачивание.

ПРИЛОЖЕНИЕ 1.

Альтернативный подход состоит в использовании локальной интерполяции, когда функция интерполируется многочленом невысокой степени на отрезке малой длины, содержащимся в [a,b]. При этом используется лишь часть табличных значений.

ПРИЛОЖЕНИЕ 2.

ПРИМЕР.11.4. Функция y=y(x) задана таблицей своих значений:

x	0	0.2	0.4	0.6	0.8
y	7	5	2.5	1.7	1.25

Требуется найти значения функции в точках 0.38, 0.7, 0.79

Построим диагональную таблицу конечных разностей:

0 7

-2

0.2 5 -0.5

-2.5 2.2

4. 2.5 1.7 -3.55

-0.8 -1.35

0.6 1.7 0.35

-0.45

0.8 1.25

Рассмотрим интерполяцию локальными многочленами 2-ой степени:

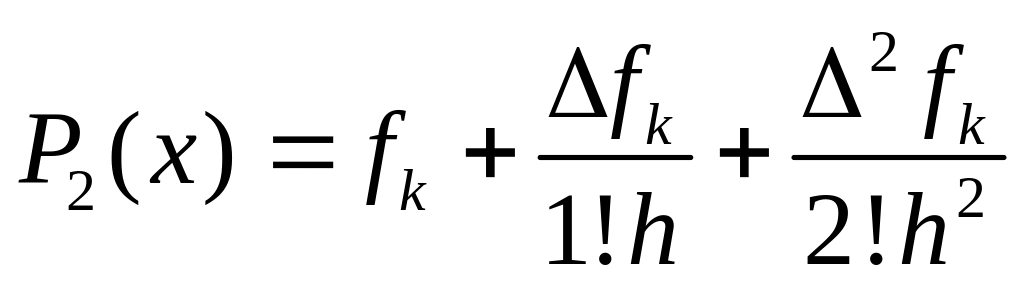, при использовании на отрезке .

Для точки x=0.38 имеет смысл взять в качестве узлов интерполяции точки 0.2, 0.4,0.6

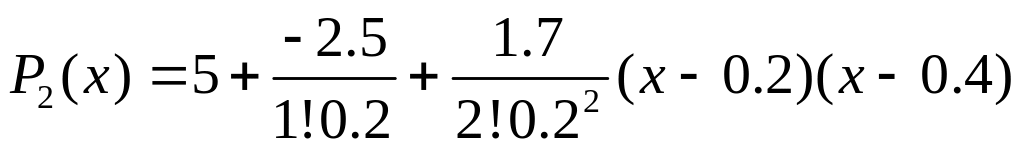
Для точек 0.7 и 0.79 можно использовать точки 0.4,0.6,0.8:

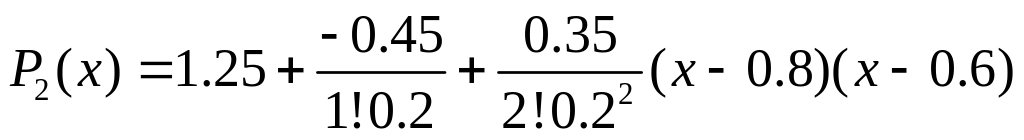
§11.4 Интерполяция c кратными узлами.

Пусть в узле известны не только значения функции , но и значения ее производных , , … до некоторого порядка k.

В этом случае узел называют кратным, а число k+1,равное количеству заданных значений, называют кратностью узла.

Пример. Пусть дана точка и в ней заданы значения: .Тогда многочлен , удовлетворяющий условиям , , … представляется в виде отрезка ряда Тейлора:

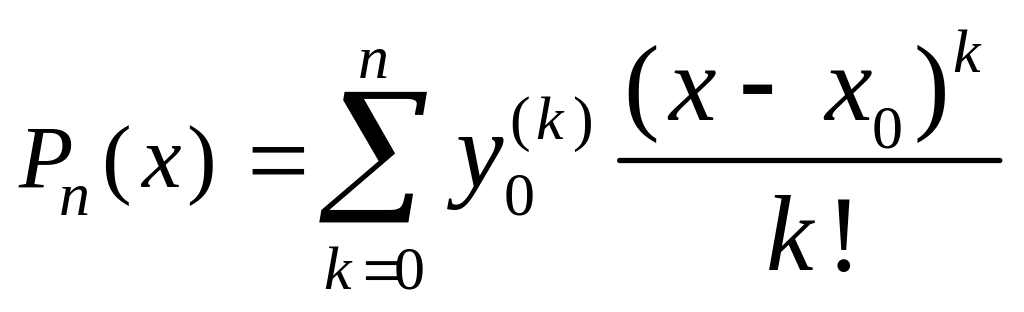(11.9)

Таким образом, формула Тейлора дает решение задачи интерполяции с кратным узлом.

ПОСТРОЕНИЕ МНОГОЧЛЕНА ЭРМИТА

Рассмотрим отрезок интерполяции . Будем считать, что длина отрезка , и в концах отрезка известны не только значения функции и , но и значения производных: и , то есть оба узла кратности 2.

Построим многочлен , удовлетворяющий условиям:

, , , (11.10)

Запишем многочлен в общем виде:

Для определения коэффициентов воспользуемся равенствами (11.10)

,

,

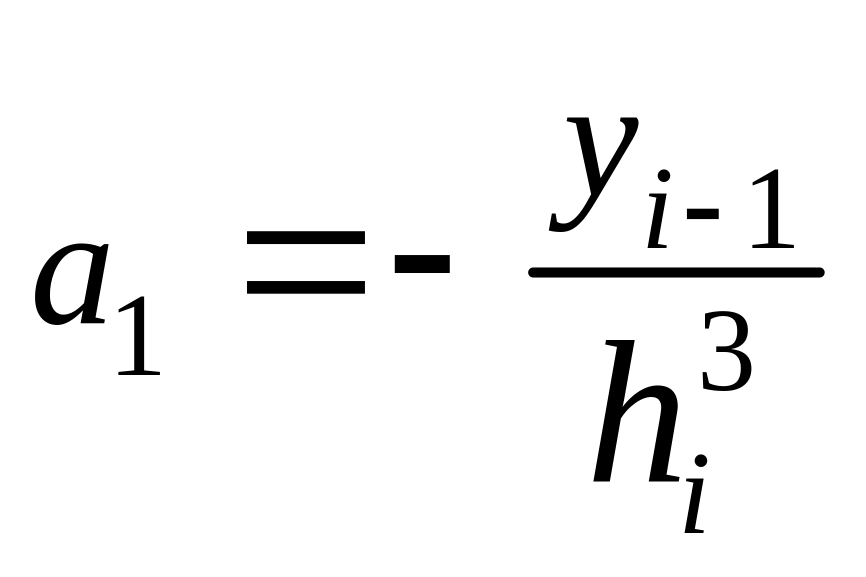
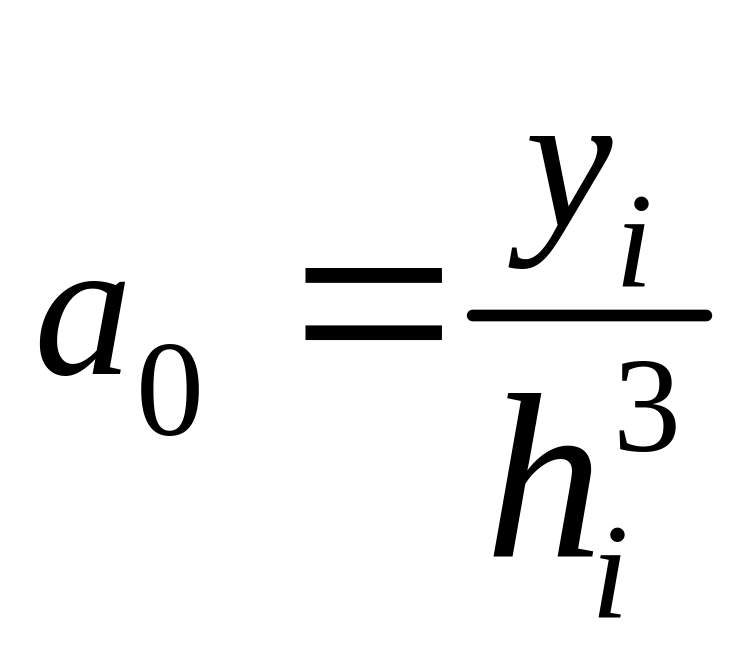
Продифференцируем исходный полином:

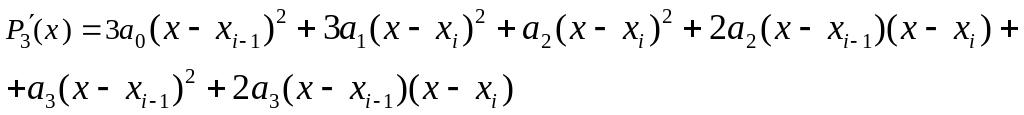
Теперь подставим значения узлов и значения производных:

,

,

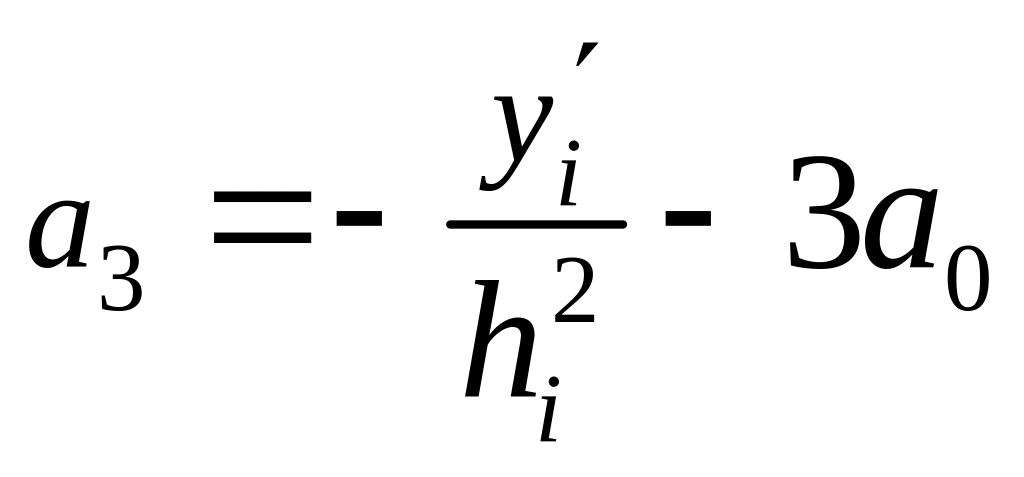
Таким образом, интерполяционный многочлен примет вид:

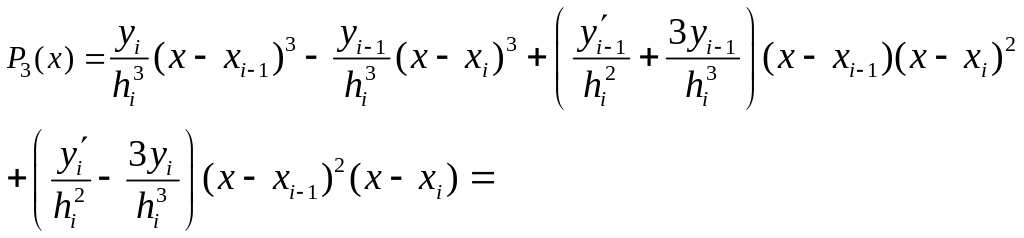
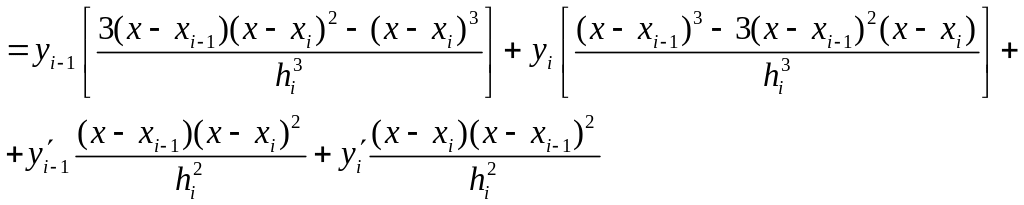Выполним последнее преобразование:

Аналогично преобразуем другое слагаемое:

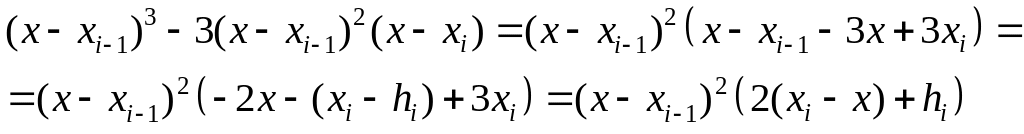
Окончательно, полином запишется так:

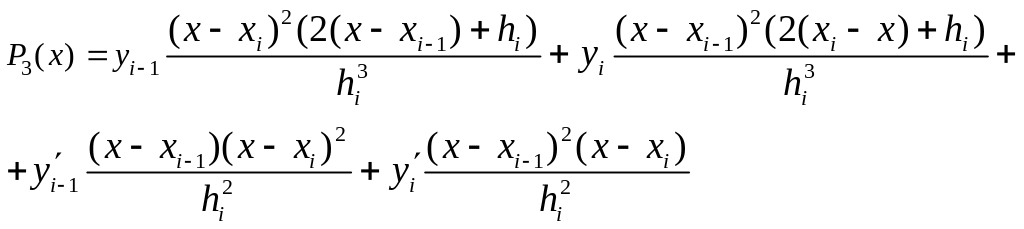(11.11)

Полученный полином называется полиномом Эрмита.