
ЛЕКЦИЯ 5. Прямые методы решения систем линейных алгебраических
уравнений (СЛАУ)
ЛИТЕРАТУРА. Учебник [1] §5.1. §5.5, §5.6, §5.7.
§ 5.1 Постановки задач.
Д
(5.1)
 ана
система линейных уравнений (СЛУ) с m
неизвестными:
ана
система линейных уравнений (СЛУ) с m
неизвестными:
В матричной форме записи система (5.1) имеет вид:
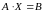 (5.2)
(5.2)
где: m – порядок системы;
 – матрица
коэффициентов системы;
– матрица
коэффициентов системы;
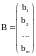 – вектор свободных
членов;
– вектор свободных
членов;
 – вектор неизвестных;
– вектор неизвестных;
В свернутой форме записи СЛУ имеет вид:
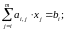
 (5.3)
(5.3)
Система называется невырожденной, если определитель системы
0, и тогда система (5.1) имеет единственное решение.
Система называется вырожденной, если = 0, и тогда система (5.1) не имеет решений или имеет бесконечное множество решений.
Ниже будут рассматриваться невырожденные системы уравнений.
Напомним, что мы рассматриваем прямые и итерационные методы решения задач.
Опр. Метод называется прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций.
Итерационный метод строит последовательность приближений к решению.
Для решения СЛУ применяются прямые и итерационные методы. Область применения некоторых из них показана в таблице.
Тип |
Название метода |
Число арифметических действий (при n = 20) |
Область примененения |
Прямые |
Формулы Крамера |
~
|
n<5 |
Исключения Гаусса |
~
|
n<200 |
|
Итерационные |
Простых итераций |
~ n² на каждой итерации (400n) |
до 105 |
Гаусса-Зейделя |
Если современная супер-ЭВМ имеет производительность 30 терафлоп – 30·1012 операций с вещественными числами в секунду. Такой машине для решения СЛУ для n=20 по формуле Крамера требуется:
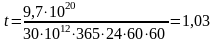 года.
года.
На решение СЛУ прямым методом сильное влияние оказывает погрешность округления, т.к. требуется огромное количество арифметических действий.
На решение СЛУ итерационным методом погрешность округления практически не влияет, но не всегда удается обеспечить сходимость итерационного процесса.
§ 5.2 . Метод исключения неизвестных (метод Гаусса).
Решим систему методом исключения Гаусса.
Пример 5.1. Решение проводиться в два этапа.
1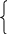 этап Прямой
ход -
матрица A
преобразуется к треугольному виду:
путем эквивалентных линейных преобразований
уравнений системы поддиагональные
коэффициенты матрицы А обнуляются.
этап Прямой
ход -
матрица A
преобразуется к треугольному виду:
путем эквивалентных линейных преобразований
уравнений системы поддиагональные
коэффициенты матрицы А обнуляются.
x1 + 5x2 - x3 = 2
x1 2x3 = -1
2x1 - x2 – 3x3 = 5
И сключим x1 из 2-го и 3-го уравнения: ко 2-му уравнению прибавим 1-ое, умноженное на (-1); к 3-му уравнению прибавим 1-ое, умноженное на (-2).
x1 + 5x2 - x3 = 2
- 5x2 + 3x3 = -3
- 11x2 – x3 = 1
Исключим x2 из 3-го уравнения: к 3-му уравнению прибавим 2-ое, умноженное на (-11/5). Полученный вид системы после прямого хода
x 1 + 5x2 - x3 = 2
- 5x2 + 3x3 = -3
– 38/5x3 = 38/5
2 этап Обратный ход - вычисляются значения неизвестных, начиная с последнего уравнения:
x3* = -1
-5x2 + 3x3*=-3 x2*=(3 + 3x3*)=(3 + 3(-1))=0
x1 +5x2* - x3*=2 x1*=2 + 5x2* + x3*=2 + 50 + (-1)=1
Полученное решение нужно обязательно проверить, подставив в исходную систему!
Проверим полученное решение подстановкой в исходную систему.
1 + 50 – (-1) = 2
1 + 2(-1) = -1
21 – 0 – 3(-1) = 5
Система обращается в тождество, решение верное
Рассмотренный вариант метода Гаусса называется схемой единственного деления. Опишем «словесно» данный алгоритм.
Прямой хода метода:
Шаг 1. Пусть a11 ≠ 0. Будем называть a11 «ведущим» элементом первого шага
Найдем величины,
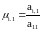 ,
,
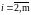 - масштабирующие множители 1-го шага.
Выполним преобразование:
- масштабирующие множители 1-го шага.
Выполним преобразование: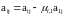
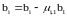 , то есть последовательно вычтем из 2,
3,…строк 1-ую строку, умноженную на
соответствующие множители
, то есть последовательно вычтем из 2,
3,…строк 1-ую строку, умноженную на
соответствующие множители
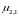 ,
,
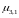 ,
…
,
…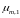 . После 1-го шага система примет вид:
. После 1-го шага система примет вид:
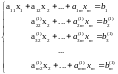 (5.4)
(5.4)
2. k-ый
шаг метода. Пусть
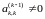 тогда это ведущий элемент k-ого
шага
тогда это ведущий элемент k-ого
шага
Для строк i=k+1, k+2, …, m вычисляются значения множителей k-ого шага
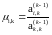 ,
,
 ,
и новые правые части
,
и новые правые части

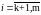
После выполнения (m-1)шага метода Гаусса система приводится к треугольному виду:
 (5.5)
(5.5)
Алгоритм обратного хода:
Вычислим

Остальные переменные вычисляем по формулам:
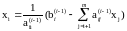 ,
,

§ 5.3 LU- разложение матрицы.
Схему Гаусса можно записать в матричной форме. Выполнение прямого хода метода Гаусса сводится к последовательному умножению системы уравнений на матрицы следующего вида:
 ,
,
 ,
…
,
…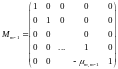
называемыми элементарными матрицами.
Легко проверить,
что после 1-го шага исключения система
преобразуется к виду (5.4), который может
быть получен как

На следующем шаге
умножаем то, что получилось на матрицу
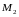 :
:
 .
.
Таких умножений сделаем m-1. Тогда система примет вид:
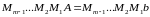
Вид этой системы приведен в (5.5) Матрица системы является
верхней треугольной. Обозначим эту матрицу U от (англ. Upper)
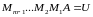
Тогда используя понятие обратной матрицы и ее свойства, имеем:
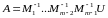
Если исследовать свойства элементарных матриц, то очевидно, что они все невырожденные и нижние треугольные. Произведение нижних треугольных матриц дает нижнюю треугольную матрицу . Кроме того, легко проверить, что обратные к элементарным матрицам имеют вид:
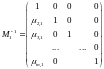
 ,
,
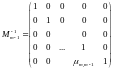
Тогда результирующая обратная матрица оказывается равной:
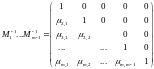
Эту матрицу будем обозначать дальше L ( от англ.Low – нижний).
Тогда получим так называемое LU- разложение матрицы А=LU.

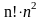 (
(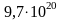 )
)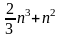 (5733)
(5733)