Пример 5.2.

Рассмотрим решение задачи методом Гаусса и методом LU- разложения.

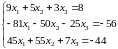
Запишем расширенную матрицу системы:

1 шаг метода: - исключаем неизвестные из всех уравнений кроме 1-го:

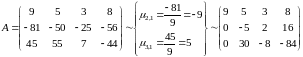
2 шаг метода. Ведущий элемент 2-го шага -5 :

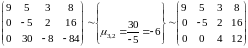
Таким образом, систему привели к верхнему треугольному виду:

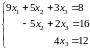
Обратный ход метода Гаусса (снизу вверх):

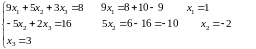
Теперь не выполняя дополнительных действий, запишем LU- разложение матрицы:

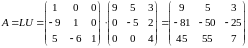
Заметим, что для разложения матрицы на множители нам не потребовался столбец b.

Теперь запишем систему как: LUx=b и для удобства введем

вспомогательный вектор y=Ux. Тогда систему можно решать в 2 этапа:

Ly=b и найти отсюда y

Затем:

Ux=y

Обе системы простой структуры: первая – нижняя треугольная, вторая – верхняя треугольная. Решение легко находится:

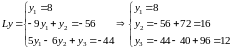
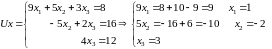
Трудоемкость метода Гаусса – количество арифметических действий:

( , )

Прямой ход требует:

1 шаг 2-ой шаг m-1 – шаг:

Делений m-1 m-2 1

Умножений (m-1)² (m-2)² 1

Вычитаний (m-1)² (m-2)² 1

Общее число арифметических действий:

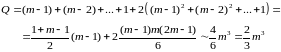
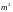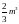Для реализации обратного хода метода требуется всего арифметических действий. Этим значением можно пренебречь. Поэтому считается, что метод Гаусса требует арифметических действий. Заметим, что LU- разложение матрицы требует такого же количества действий при однократном решении системы. Но если применять метод многократно, то можно получить существенную экономию арифметических действий.

Обычно LU- разложение применяется в случае, когда мы имеем несколько систем уравнений с разными правыми частями, но с одной и той же матрицей A.

, , …

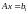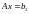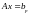
Можно один раз выполнить разложение матрицы на множители, то есть найти

LU-разложение, а затем решать p простых систем.

Пример 5.3. Пусть даны 2 системы уравнений:

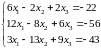
Выполним LU- разложение матрицы

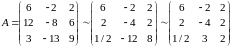
Таким образом, получили:

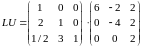
Дальше решаем 2 пары систем:

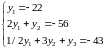
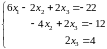
Тогда :

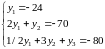
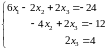
Тогда :

Модификации метода Гаусса.

Первая модификация метода Гаусса – схема частичного выбора.

На каждом шаге метода выбирается максимальный элемент по модулю в k-ом столбце.

Затем строки меняются местами и выполняется преобразование Гаусса. Этот дополнительный

прием позволяет избежать нулевых ведущих элементов и ведет к вычислительной устойчивости метода.

Преобразование элементов матрицы выполняется по формуле:

Масштабирующие множители по модулю все меньше или равны 1, следовательно, при преобразовании Гаусса погрешность не увеличивается.

Вторая модификация – схема полного выбора. На каждом шаге выбирается максимальный по модулю

элемент по всей подматрице ( на 1-ом шаге – по всей матрице.). Далее строки и столбцы меняются местами так, чтобы максимальный элемент стал ведущим. И выполняется шаг метода. Схема также устойчива, но при этом нужно следить за нумерацией неизвестных.

Более подробно можно посмотреть в учебнике [1] в § 5.5.