Отклонения толщины фоторезиста от среднего значения при различных частотах вращения центрифуги

Часто­та вра­щения, мин^-1	Наблюдения								Сумма	Число наблю­дений	Среднее арифме­тическое значение
	1	2	3	4	5	6	7	8
1000 2000 3000	0,16 0,04 0,06	0,06 0,12 0,02	0,18 0,14 0,06	0,22 0,04 0,06	0,12 0,06 0,04	0,22 0,14 0,04	0,20 0,06 0,02	0,06 0,08 0,06	1,12 0,68 0,36	8 8 8	0,140 0,085 0,045
									= = 2,16	N=24	= =0,09

Регрессия и корреляция. До сих пор обсуждаемые методы обработки данных касались только одного признака. Теперь рассмот­рим случай, когда у изделия замеряются два различных признака: X и Y. При этом могут возникнуть следующие варианты.

1. Оба признака X и У тесно связаны друг с другом (например, электрический ток и напряжение в законе Ома). Этот вид связи называют функциональным. Зависимость между обоими признаками выражается в виде формулы. Поэтому при функциональных связях каждому определенному значению x соответствует одно или несколько значений у, и наоборот. Примерами функциональных связей i являются все точные законы астрономии, механики, физики и химии.

2. Оба признака X и У не строго связаны между собой, и связь эта не функциональная, а статистическая. В этом случае каждому фиксированному значению х соответствует ряд изменяющихся вместе с изменением X значений Y и, наоборот, каждому фиксированному значению у соответствует ряд значений X, которые тоже изменяются с изменением Y.

3. Оба признака X и Y не связаны между собой. В этом случае значения признака Y не меняются с изменением X, и наоборот. Таким образом, оба признака X и Y не зависят друг от друга.

При управлении качеством желательно знать не только зависимость друг от друга двух или нескольких количественных признаков, но и вид связи между ними и насколько тесна эта связь. Решение этого вопроса имеет большое значение для контроля в управления качеством объекта.

Связь между двумя количественными признаками проявляется в виде определенной тенденции, например, если один признак уве­личивается, то другой увеличивается или уменьшается.

Учитывая, что при статистических связях каждому фиксирован­ному значению одного признака соответствует распределение другого признака, можно, подсчитав среднее арифметическое этого распределения, представить эту связь в виде зависимости среднего арифметического значения одного признака, например параметра качества , от другого признака (фактора) X.

Статистическую связь, представленную в таком виде, называют корреляционной связью Y с X. Точно так же корреляционной связью X с Y называют связь статистических средних признака X, вычисленных для различных значений признака Y. Корреляционная связь с X выражается в общем виде следующим уравнением:

= f (x), (2.57)

а связь с Y – соответственно

= φ (y) (2.58)

Уравнения (2.57) и (2.58) называют уравнениями регрессии или корреляционными уравнениями, причем уравнение (2.57) — уравне­нием регрессии У на X, а уравнение (2.58) — уравнением регрессии X на Y. Вид функций f(x) и φ (у) в этих уравнениях зависит от формы связи рассматриваемых признаков.

Таким образом, уравнение регрессии отображает форму связи и дает ответ на вопрос, является ли корреляционная связь прямоли­нейной или криволинейной.

На практике связь между двумя признаками в интересующей области может быть линейной или приблизительной линейной. В тех случаях, когда она нелинейная, часто путем преобразования (логарифмированием, извлечением корня и т. п.) одного из призна­ков можно произвести линеаризацию характера кривой. Кроме того, практически любая нелинейная зависимость может быть раз­делена на участки с линейной зависимостью рассматриваемых при­знаков. «Наилучшая» прямая, выравнивающая опытные данные, определяется методом наименьших квадратов.

Если наблюдаемые значения признаков обозначить через (x₁ , y₁), (x₂ , y₂),… (x_n , y_n), то прямая регрессии Y на X запишется в виде

у= +b(х- ). (2.59)

где — средняя арифметическая значении y₁ ,у₂ ,…, у_п ; — средняя арифметическая значений x₁ ,х₂,…х_n ; Y определяет ординаты точек вычисленной прямой в зависимости от значений признака.

Коэффициент b в уравнении (2.59) называют коэффициентом регрессии Y на X и определяют по формуле

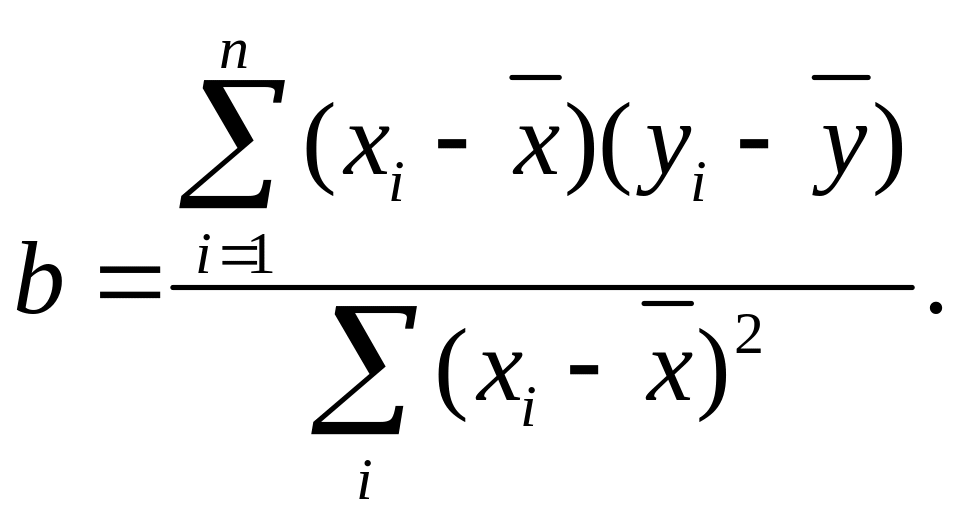
Если рассматривать характер изменения X по Y, т. е. считать, что X зависит от значений признака Y, то прямая регрессии X на Y будет иметь вид

х= +b'(у- ) (2.60)

где

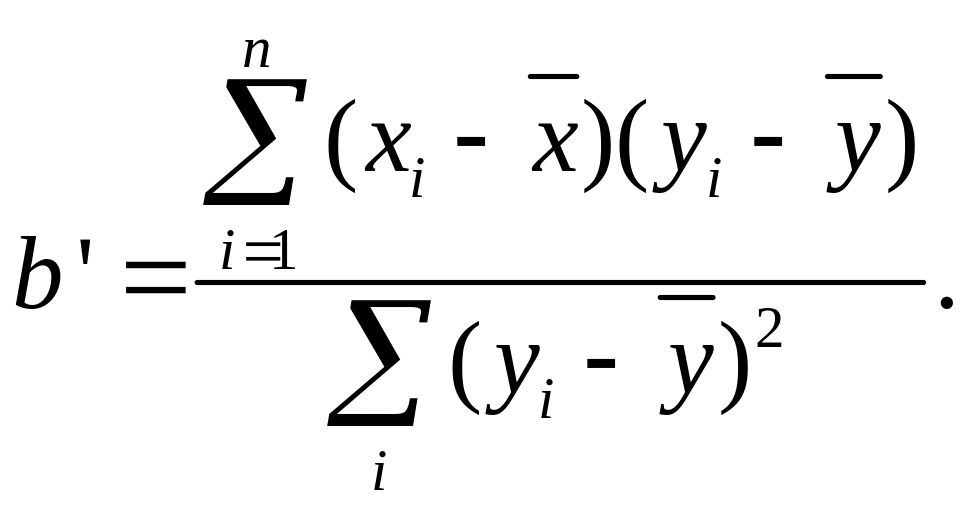
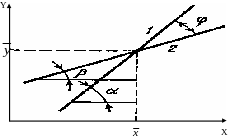
Рис. 2.8. Графическое изображение прямых регрессии Y на X(1) и X на Y(2).

Оба уравнения регрессии не эквивале­нтны, так как b' ≠ 1/b. Итак, прямая ре­грессии Y на X не совпадает с прямой регрессии X на Y, хотя обе они проходят через точку с координатами ( , ). Гра­фическое изображение регрессии предста­влено на рис. 2.8.

Коэффициент регрессии Y на X равен тангенсу угла между прямой регрессии и осью x(tgα), а коэффициент регрессии X на Y — котангенсу угла между прямой регрессии и осью х(ctgβ), т.е.

tgα = b,

tg β = 1/ ctgβ = 1/b'

Полученные две прямые регрессии отражают различный подход к проблеме. В первом случае по известному значению X получаем оценку для Y, а во втором — по известному значению Y получаем оценку для X. Соответственно находим минимум суммы квадратов отклонений по вертикали и по горизонтали.

Если форма связи рассматриваемых признаков определяется i видом уравнения регрессии, то степень связи определяется коэффициентом корреляции r, который вычисляется по формуле

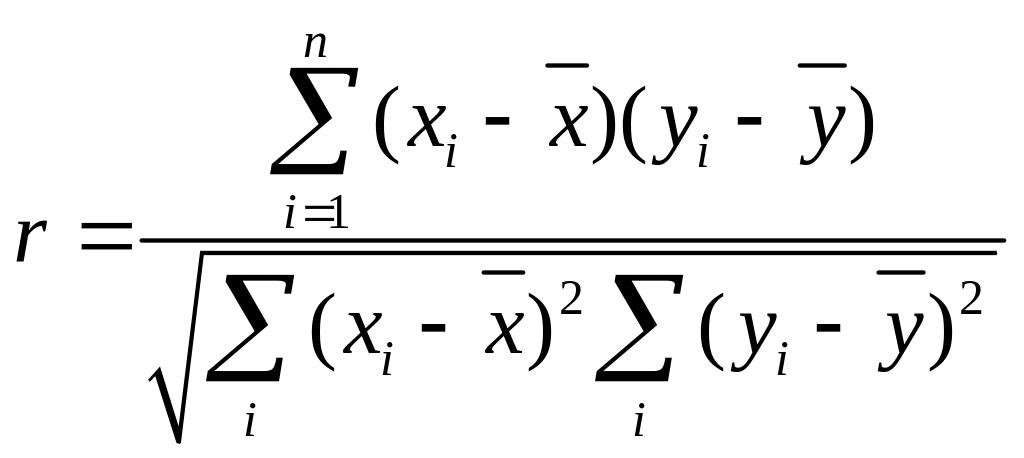(2.61)

Из сравнения (2.61) с выражениями для b и b' нетрудно увидеть, что

(2.62)

На основании (2.62) можно сделать вывод, что при равенстве углов α и β (что имеет место при совпадении прямых регрессии Y на X и X на У, т. е. при функциональной связи между признаками X и. Y) r = ± 1.

Если г>0, то линейная функциональная связь прямая (с ростом значений X увеличивается Y, и наоборот); если г<0, то связь обратная (с ростом значений X значения Y уменьшаются).

В статистическом наблюдении функциональная зависимость превращается в корреляционную (ибо в этом случае мы имеем дело со случайными величинами), поэтому углы наклона прямых регрес­сии Y на X и X на Y будут отличаться, причем разность между углами α и β (т. е. угол φ между прямыми регрессии) тем больше, чем меньше единицы абсолютное значение коэффициента корреля­ции, и, наконец, при r=0 имеем угол φ = 90°, что означает полное отсутствие прямолинейной корреляционной связи между рассмат­риваемыми признаками X и Y. Но это еще не значит, что будет отсутствовать криволинейная корредяционная связь между рассма­триваемыми признаками. Таким образом, коэффициент корреляции принимает значения от — 1 до +1.

При оценке самого коэффициента корреляции учитывается число пар наблюдений п, по которым было произведено его вычисление. При небольшом числе пар величина г часто значительно отличается от его действительного значения. Поэтому нужен критерий, кото­рый установит, случайно ли отклоняется коэффициент корреляции от нуля или имеется корреляционная связь.

Для этого вычисляют

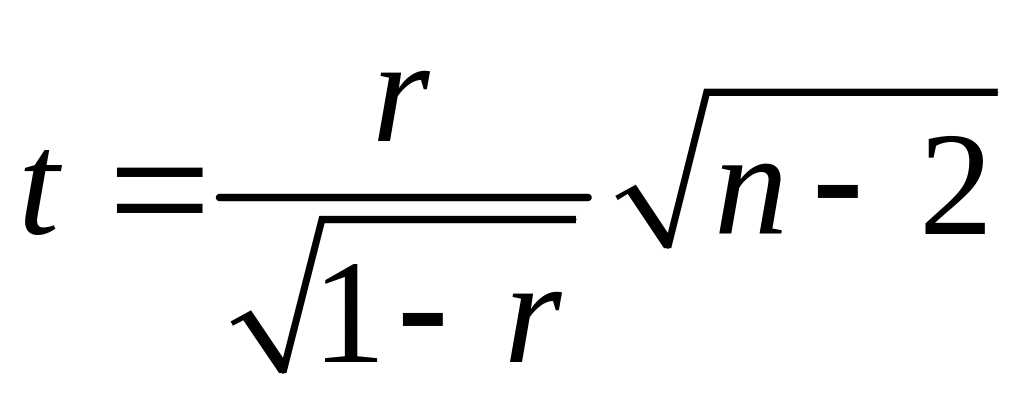(2.63)

и оценивают полученное значение t с числом степеней свободы υ=n — 2. Если t<t_T (см. табл. 4 Приложения [3, с. 406]), то корреляция между рассматриваемыми признаками существует.

Пример 6. В качестве примера исследуем связь между размахом R и стандартным отклонением s выборок одинакового объема. Для этого отберем 50 выборок объ­емом n = 5 из объекта М(х) = 50, σ = 5. Для каждой выборки вычислим размах R (признак х) и стандартное отклонение s (признак у). Выборки расположим в поряд­ке возрастания s (табл. 2.10).

Таблица 2.10

Результаты расчета размаха и стандартного отклонения

Номер выбор ки	xi(R)	хi -	yi (s)	yi -	(хi- )· (yi - )	(хi - )^2	(yi- )^2
1 2 3 . .	6 6 5 . .	-5,46 -5,46 -6,46 . .	2,345 2,491 2,510 . .	2,441 2,367 2,286 . .	13,328 12,924 14,768 . .	29,81 29,81 41,73 . .	5,958 5,603 5,226 . .
49 50	17 24	5,54 12,54	7,944 10,124	3,158 5,338	17,485 66,938	30,69 157,25	9,973 28,494
	573		239,284		334,15	806,34	147,217

= 11,46; = 4,786

Какого значения признака Y(стандартное отклонение s) можно ожидать при известном независимом значении признака X (размах R)? Ответить на поставленный вопрос можно, если использовать полученное в результате вычислений уравнение

Зависимость признака X (размах R) от признака Y (стандартное отклонение s) получим из другого уравнения регрессии:

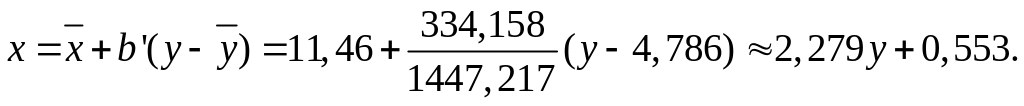
Подставив числовые значения в выражение (2.61), получим

Далее с помощью выражения (2.63) находим

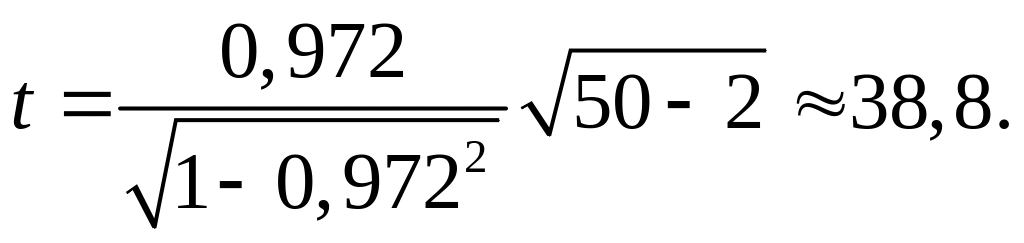
Эго значение оказывается меньше, чем t_т для β=0,01 и n-2=48, найденного из табл. 4 Приложения [1, с. 406], поэтому корреляция между R и s существует.

В случае криволинейной связи между двумя признаками оценка силы корреляционной связи между ними осуществляется с помо­щью корреляционного отношения. Так, для корреляционной связи X и У корреляционное отношение имеет вид

(2.64)

где k — число выборок; — общая средняя арифметическая: N — oбщее число наблюдений в k опытах.

Аналогично для корреляционного отношения Xи Убудем иметь

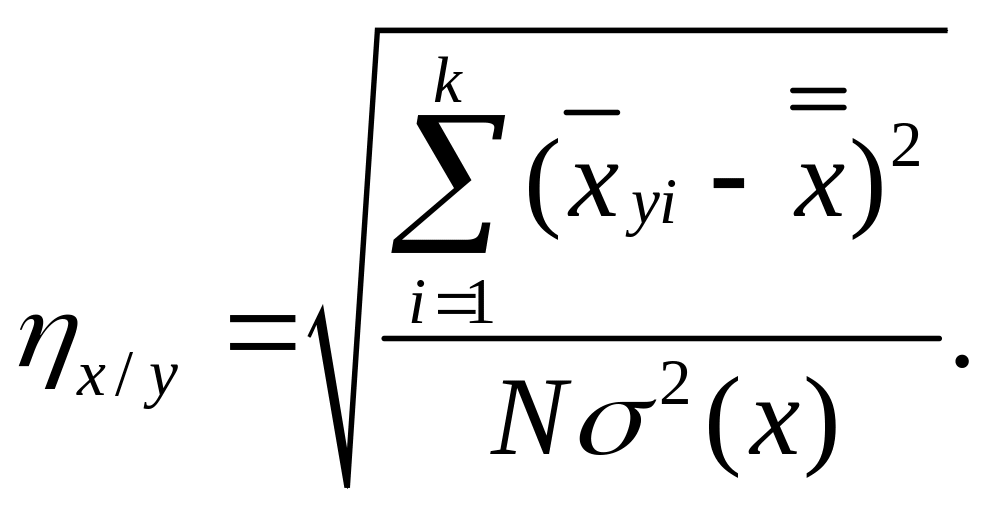(2.65)

Если учесть, что подкоренные выражения

и

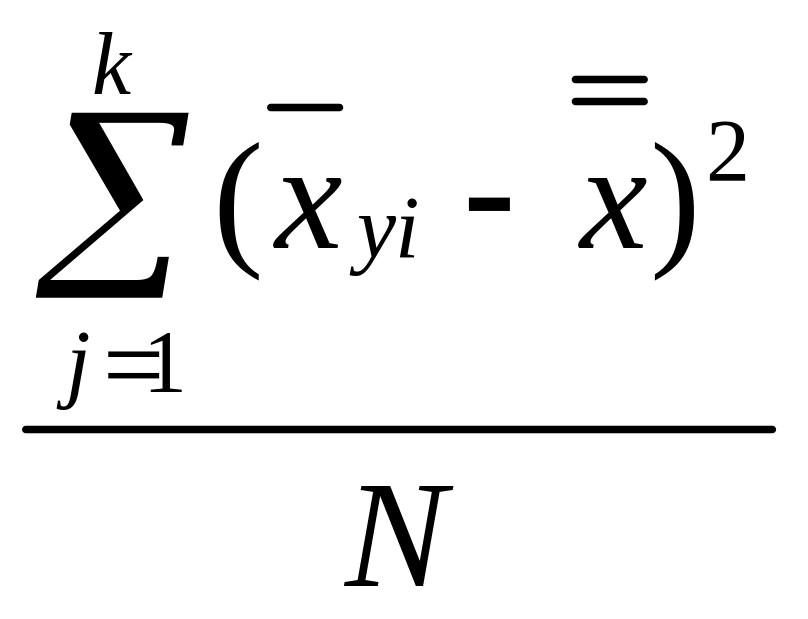
есть нечто иное, как дисперсия средних арифметических около общих средних, т. е. σ_у²и σ_x²т.е. соответственно, то выражения для корреляционных отношений (2.64) и (2.65) можно переписать в сле­дующем виде:

(2.66)

(2.67)

Величина корреляционного отношения меняется в следующих пре­делах:

0 ≤ η ≤ 1 (2.68)

Если признаки связаны однозначной функциональной связью, то η =1. Если же какая-либо связь между ними отсутствует, то η =0. При этом значение корреляционного отношения всегда не меньше абсолютного значения коэффициента корреляции, т. е. η ≥ | r |. Если η = | r |,то это является необходимым и достаточным условием, что корреляционная связь двух рассматриваемых признаков является линейной.

Контрольные вопросы

1. В каком случае выборку можно считать репрезентативной?

2. Что понимается под статистическим рядом и какие его разновидности вам известны?

3. Приведите примеры дискретного и непрерывного изменений случайной вели­чины.

4. Как составляется и в дальнейшем заполняется контрольный лист?

5. Какие числовые характеристики статистического ряда вам известны?

6. В чем отличие генеральных и выборочных характеристик?

7. Поясните порядок построения наиболее распространенных графиков пред­ставления статистического ряда.

8. Назовите все три условия центральной предельной теоремы.

9. Всегда ли колоколообразное симметричное распределение случайной вели­чины описывается законом Гаусса и как это можно проверить?

10. Объясните понятие «область статистического допуска» на контролируемый параметр качества.

11. Какие критерии статистической проверки гипотез вам известны и в чем их смысл?

12. Как подсчитать дисперсии между выборками, внутри выборки и общую? Что при этом понимают под числом степеней свободы?

13. Можно ли утверждать, что при коэффициенте корреляции, равном нулю, отсутствует корреляционная связь между рассматриваемыми признаками?