Учебное пособие 1692

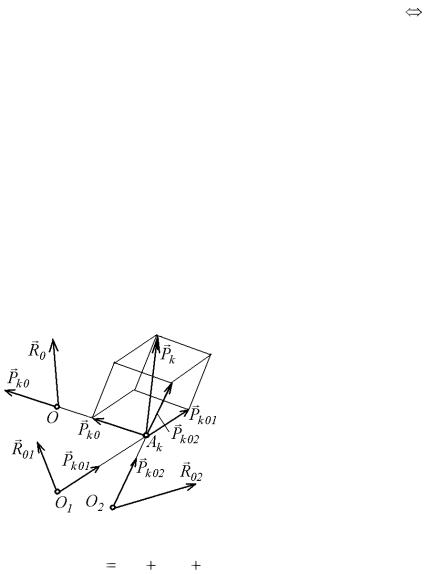
Две системы сил называют эквивалентными, если они, будучи приложенными поочередно, порознь, к одному и тому же абсолютно твердому телу вызовут одинаковое действие на тело. Эквивалентность систем сил обозначается символом . Замена исходной системы сил другой эквивалентной системой позволяет иногда существенно упростить исследование равновесия или движения тела. Более подробные сведения о преобразованиях эквивалентных систем сил приведены в гл. 9.

Теорема 8.1 о приведении произвольной системы сил к двум силам. Система сил, произвольно расположенных в пространстве, эквивалентна двум силам, одна из которых приложена в произвольной точке. Главный вектор и главный момент этой системы сил относительно этой точки соответственно равны главному вектору и главному моменту эквивалентной системы двух сил относительно той же точки.

Доказательство. Разделим доказательство теоремы на два этапа. Вначале заменим данную систему сил тремя эквивалентными силами, а затем покажем, что три силы всегда можно заменить двумя силами.

Возьмем три произвольные точки О, O1, O2..

				Соединим эти точки прямы-
				ми с точками приложения Ak
				всех сил системы (рис. 8.1),
				где k - порядковый номер
				точки приложения силы Pk .
				Тогда каждую силу Pk , со-
				гласно правилу параллеле-
	Рис. 8.1			пипеда, можно разложить по
				трем направлениям OAk ,
	O1Ak и O2Ak Pk	Pko	Pko1	Pk02 .

Согласно теореме Вариньона (§ 7.6)

136

M0	( Pk ) M0		( Pko ) M0 ( Pko1 ) M0				( Pko2 ) .
Перенесем все составляющие силы Pko , Pko1								и Pk o2 по их
линиям действия соответственно в точки О, O1 и O2 . Получаем
три пучка сил: один пучок из сил					Pk o , приложенных в точке О,
второй пучок из сил Pk o1				приложенных в точке O1				и третий
пучок из сил Pk o2		приложенных в точке O2. Равнодействую-

щие сил, образующих каждый пучок сил, соответственно будут равны

	R0	Pko ;	R01		Pko1 ; R02					Pko 2 .
	Согласно теореме Вариньона (§ 7.6),
			M0 ( R0 )				M0 ( Pko ) ;
	M0 ( R01 )		M0 ( Pko1 );				M0 ( R02 )			M0 ( Pko2 ) .
	Итак, заданная система сил приведена к эквивалентной
системе из трех сил R0				, R01, R02			. Главные вектор и момент по-
лученной системы сил равны
	V0	Pk	( Pk0		Pko1		Pko 2 )			Pk0	Pk01
			Pk 02		R0		R01	R02 ,			(а)
M0	M0 ( Pk )		[ M0 ( Pko )				M0 ( Pko1 ) M0 ( Pko 2 )]
	M0 ( Pko )			M0 ( Pko1 )				M0 ( Pko2 )
		M 0 ( R0 ) M 0 ( R01 ) M 0 ( R02 ) .									(б)

Итак, главный вектор заданной системы сил равен главному вектору эквивалентной системы из трех сил, приложенных в точках О, O1 и O2, а главный момент заданной системы

137

сил относительно точки О равен главному моменту относительно той же точки эквивалентной системы из трех сил.

Покажем, что систему трех сил можно заменить двумя сила-

ми. Имеем три силы: R0 , R01 , R02			,

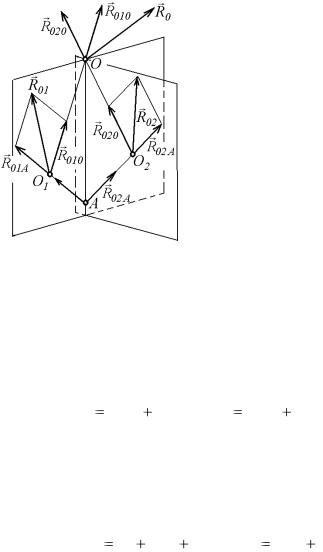
приложенные соответственно в точках О, O1 и O2. Проведем через точку О две плоскости так, чтобы

одна плоскость проходила через

линию действия силы R01 , а дру-

гая - через R02 . Такое построение

	Рис. 8.2			всегда возможно (рис. 8.2). На ли-
				нии пересечения плоскостей возь-
мем любую точку А и соединим ее прямыми с точками O1 и O2.
Затем разложим силу			R01 по направлениям O1O и O1А, а силу
R02 разложим по направлениям O2O и О2А.
	Тогда
	R01	R01O	R01A ,	R02	R02O	R02A .	(в)
	Перенесем по линиям действия составляющие						R01O и
R02O	в точку приложения О, а составляющие R01A и R02A в

точку приложения А. Затем складывая силы, приложенные в точках О и А, получаем

	*							.	(г)
R		R R		R , R		R	R
0		0	010	020		A 01A	02A

Итак, исходная система сил приведена сначала к эквивалентной системе из трех сил, а затем к эквивалентной системе

из двух сил:		*			(рис. 8.3). Учитывая (а), (в) и (г), полу-
	R		и R	A
	0
чаем
					138

Рис. 8.3

M 0

VO	R0	R01	R02	R0	R010	R01A

			*			.
R	R	R		R	A
02O	02A	0

Следовательно, главный вектор данной системы равен главному вектору эквивалентной системы из двух сил, из которых одна приложена в произвольной точке О.

Далее, с учетом (б), (в) и (г), получаем

M 0 ( RO ) M 0 ( RO1 ) M 0 ( RO2 ) M 0 ( RO )

M0 ( RO10 )		M0 ( RO20 )		M0 ( RO1A )

				*				).
M	( R	) M	( R		) M	( R	A
0	O2 A	0	O		0

Следовательно, главный момент заданной системы сил относительно произвольно выбранной точки О равен главному моменту относительно той же точки эквивалентной системы из двух сил. Теорема доказана.

§ 8.2. Условия равновесия абсолютно твердого тела

При доказательстве теорем обычно употребляют формулировку: «необходимое и достаточное условие». Теоремой, обратной данной (прямой теореме), называют такую теорему, условием которой служит заключение данной теоремы, а заключение - условием данной теоремы. Если прямая теорема верна, то обратная теорема может быть как верна, так и не верна. Поэтому истинность обратных теорем подлежит доказательству.

Прямой назовем теорему, содержащую так называемое необходимое условие. Введем для сокращения записи буквенные обозначения. Пусть выполнение некоторого события (явления, свойства и т.д.) обозначим буквой А. Тогда необходимым условием для события А является такое событие В, кото-

139

рое всегда вытекает, следует из события А. Запишем условно А В. Например, пусть событием А является дождь. Тогда не-

обходимым условием В для события А (дождя) является облачное небо, так как, если идет дождь, то небо облачное. Но для обратной теоремы это утверждение неверно, так как если на небе облака, то это недостаточное условие для дождя: дождя может и не быть. В нашем примере из А следует В, но из В может и не следовать А.

Таким образом, из необходимого условия В еще не следует существование условия А. Достаточным условием для события А является такое событие В, из которого всегда следует событие А. Условная запись: А В.

Например, пусть событием А является то, что на улице светло. Тогда солнечный день является достаточным условием

Вдля события А. Но это условие не является необходимым, так как оно может не выполняться, например - солнце не светит, а на улице все же светло из-за электрического освещения.

Внашем примере из события В следует событие А, но если событие В не выполняется, то событие А может все же выполняться.

Приведем другой пример: для четности числа достаточно, чтобы оно делилось без остатка на четыре. Здесь событием А является четность числа. Достаточным условием для А является событие В, т. е. делимость числа на четыре. Действительно, если число делится на четыре, то это достаточно, чтобы оно было четным. Но делимости на четыре может и не быть, т. е. достаточное условие может не выполняться, например, число шесть не делится на четыре, а все же является четным. В этом примере достаточное условие слишком - «мощное», излишнее.

Большое значение в разнообразных исследованиях в математике, теоретической механике и многих других дисциплинах играют теоремы, которые сами верны и обратные к кото-

140

рым также верны. Это значит, что условие необходимое должно быть и достаточным.

Иногда для объединения прямой и обратной теорем в одно утверждение вместо слов «необходимое и достаточное условие» пользуются словами «в том и только в том случае...» или словами «тогда и только тогда...».

Теорема 8.2. о равновесии произвольной системы сил.

Для равновесия произвольной системы сил необходимо и

достаточно, чтобы ее главный вектор V и главный момент

M0 относительно любой точки О были равны нулю.

Доказательство необходимости. Пусть данная произ-

вольная система сил находится в равновесии. Нужно доказать,

что главный вектор V и главный

момент данной системы M0 равны

нулю. Доказательство основывается
на теореме, доказанной в предыду-
щем параграфе о том, что произ-
вольная система сил эквивалентна
		*			, из которых
двум силам: R			и R	A
		0
	*	) приложена в любой зара-
одна ( R
0

	Рис. 8.4	нее выбранной точке О, а главный
		вектор и главный момент этих двух

сил соответственно равны главному вектору и главному мо-

*

,

)

0, а отсюда

менту данной системы сил. Поэтому ( R

R

A

0

на основании второй аксиомы (рис. 8.4, а):

*

. Поэто-

R

= - R

A

0

*

му V

P

R

R

A

0 . Так как

R

и R

A

лежат, соглас-

k

0

0

но второй аксиоме, на одном отрезке прямой АО, то

141

M 0 ( R0 ) M 0 ( RA ) 0
M0		M0 ( Pk )		M0 ( R0 )		M 0 ( RA ) 0 . Необходимое ус-

ловие доказано.

Доказательство достаточности. Пусть главный вектор произвольной системы сил и главный момент этой системы относительно точки О равны нулю:

V	Pk	0 ,
M0	M0 ( Pk ) 0 .

Требуется доказать, что система сил находится в равновесии. Пользуясь теоремой о приведении системы сил к двум

силам, получаем V			RA	RA . Поскольку V		0 ,	R0	= - RA .
Тогда силы R0	и	RA	образуют пару сил (см. § 7.5). Использу-

ем теперь условие равенства главного момента системы нулю:

M0	M0	( R0 )		M0	( RA )	0 . Поскольку R0	приложена в точ-
ке О,	M 0 ( R0 )			0 . Согласно (7.17), имеем M 0 ( RA )
			0 . Векторное произведение двух векторов равно
( r	RA )

нулю или когда один из сомножителей равен нулю, или когда

перемножаемые векторы параллельны. Если RA = 0, то	R0	= -

RA = 0 и имеется равновесие, так как отсутствуют действующие силы. Если r = 0, то это означает (рис. 8.4, б), что точка А

совпадает с точкой О. Тогда обе силы, согласно второй аксио-

ме, находятся в равновесии. В случае, когда вектор r	паралле-
лен RA , это условие, учитывая, что | r | - ограниченная вели-

чина, может выполняться только тогда, когда силы R0 и RA

расположены на одной прямой. Отсюда вытекает существование равновесия. Теорема доказана.

142

Итак, получено необходимое и достаточное условие равновесия произвольной системы сил в виде двух векторных равенств:

V	Pk	0; M0	M0	( Pk ) 0 .	(8.3)

Для получения уравнений равновесия, аналогичных (8.3), в скалярной (координатной) форме, нужно спроецировать левые и правые части этих равенств на оси прямоугольной декартовой системы координат и затем использовать формулы

(7.10) и (7.25)

Vx= Pkx = 0, Vy= Pky = 0, Vz= Pkz = 0,

M Ox	npOx M 0		( Pk )	M x ( Pk	) 0 ,
M Oy	npOy M 0		( Pk )	M y ( Pk	) 0 ,
M Ox	npOz M0	( Pk )		M z ( Pk	) 0 .
Поскольку Pkx = Xk; Pky = Yk, Pkl = Zk, получаем
	X k 0;		Yk 0;	Zk	0;	(8.4)
M x ( Pk ) 0;			M y ( Pk ) 0;		M z ( Pk ) 0.

Итак, для равновесия произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил системы на каждую из трех координатных осей произвольно выбранной системы координат равнялась нулю и чтобы сумма моментов всех сил системы относительно каждой из этих осей также равнялась нулю. Рассмотрим частные случаи.

8.2.1. Система сходящихся сил.

Выберем начало координат в точке пересечения линий действия (схождения) сил. Тогда линии действия всех сил пересекают оси координат и, согласно формуле (7.23) (см. пояснения к этой формуле) моменты сил относительно этих осей

143

равны нулю. Три последние равенства (8.4) принимают вид тождеств. Поэтому

X k 0;

Yk 0;

Zk 0 .

(8.5)

Итак, для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трех координатных осей равнялась нулю.

Если все сходящиеся силы расположены в одной плоскости, то, взяв оси Ox и Oy в плоскости сил, получим, что Zk = 0, т. е. проекция любой силы на ось Oz равна нулю. Поэтому третье уравнение (8.5) тождественно удовлетворяется и его использовать нельзя.

Итак, для плоской сходящейся системы сил условия равновесия сводятся к двум соотношениям

X k 0;

Yk 0 .

(8.6)

8.2.2. Теорема о трех силах Если твердое тело находится в равновесии под действием

трех непараллельных сил, расположенных в одной плоскости, то линии действия этих сил пересекаются в одной точке.

Доказательство. Перенося две пересекающиеся силы P1

и P2 по их линиям действия в точку О их схождения, как в точку приложения, и векторно складывая, получаем равнодей-

ствующую R12		P1	P2	, которая должна уравновешиваться
третьей силой	P3	. Следовательно, согласно второй аксиоме,
линия действия силы				должна проходить через точку схож-
			P3
дения сил P1 и	P2 . Поэтому линии действия трех сил, находя-

щихся в равновесии, пересекаются в одной точке.

Использование теоремы о трех силах приведено в задаче

8.2.

144

8.2.3.Система параллельных сил, не лежащих

водной плоскости.

Проводим оси координат так, чтобы ось Oz была параллельна силам, а оси Ox и Oy были перпендикулярны силам. Тогда все силы проецируются на ось Oz в полную величину со знаком плюс или минус в зависимости от того, совпадает ли направление силы с направлением оси, или противоположно этому направлению. Проекции всех сил на оси Ox и Oy равны нулю. Также будут равны нулю и моменты всех этих сил относительно параллельной им оси Oz (см. (7.23)). Поэтому вместо

уравнений (8.4) получаем систему
Pk	0;	M x ( Pk ) 0;	M y ( Pk ) 0 . (8.7)

Итак, для равновесия системы параллельных сил, не лежащих в одной плоскости, необходимо и достаточно, чтобы сумма величин проекций этих сил на ось, параллельную этим силам, равнялась нулю и чтобы сумма моментов всех сил относительно каждой из двух координатных осей, лежащих в плоскости, перпендикулярной этим силам, также равнялась нулю.

8.2.4. Произвольная плоская система сил Выберем систему осей координат так, чтобы плоскость

(х, у) совпадала с плоскостью сил. Тогда проекции всех сил на ось Oz будут равны нулю: Zk = 0, и моменты всех сил относительно осей Ox и Oy также равны нулю, так как эти оси и силы лежат в одной плоскости. Согласно определению момента силы относительно точки (7.15) и момента силы относительно оси (7.23), в нашем случае момент силы относительно оси Oz совпадает с моментом этой силы относительно точки О - начала координат. Поэтому из уравнений (8.4) остаются три урав-

нения
X k 0;	Yk 0;	M0 ( Pk ) 0 . (8.8)
	145