Вопросы для самопроверки

1. Что такое множество?

2. Как обозначаются множества и их элементы?

3. Какими способами задаются множества?

4. Указать варианты описания множества нечетных натуральных чисел.

5. Какое множество называется пустым?

6. Что такое подмножество?

7. Какие множества называются счетными?

8. Поясните термин «мощность множества» и укажите его обозначение.

9. Что такое «универсальное « множество?

10. Перечислите операции над множествами.

11. Дайте определение объединения множеств.

12. Проиллюстрируйте с помощью диаграммы Венна операцию пересечения множеств.

13. Какие множества называются непересекающимися?

14. Дайте определение разности множеств и опишите разность множеств как множество описательным способом.

15. Дайте определение дополнения множества.

16. Можно ли определить дополнение множества, если не описано универсальное множество?

17. Перечислите законы (тождества) для операций объединения и пересечения множеств и докажите их.

18. Перечислите законы (тождества) для операции разности множеств и докажите их.

19. Перечислите законы (тождества) для операции дополнения множеств и докажите их.

Задачи по теме «Операции над множествами»

Задача 1. Укажите все собственные подмножества множества .

Ответ: , , , Ø.

Задача 2. Для каких из следующих соотношений пар множеств имеет место для множеств и ?

Ответ: .

Задача 3. Найти .

Ответ: .

Задача 4. Даны множества , , , . Задайте списками множество , , .

Ответ: , ,

.

Задача 5. Изобразите с помощью диаграмм Венна множество .

Ответ:

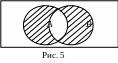
Это множество является объединением двух разностей, называется симметрической разностью и обозначается , т. е. = .

Задача 6. Опрос 100 студентов дал следующие результаты о количестве студентов, изучающих различные иностранные языки: испанский — 28; немецкий — 30; французский — 42; испанский и немецкий — 8; испанский и французский — 10; немецкий и французский — 5; все три языка — 3.

а) Сколько студентов не изучает ни одного языка?

б) Сколько студентов изучает один французский язык?

в) Сколько студентов изучает немецкий язык в том и только в том случае, если они изучают французский язык?

Указание: нарисовать диаграмму Венна в виде трех кругов, обозначающих множество студентов, изучающих соответственно французский, немецкий и испанский языки. В каждую из восьми областей вписать данные, используя приведенные цифры. Начинать с конца списка и двигаться к началу.

Ответ: а) 20; б) 30; в) 38.

2. Элементы комбинаторики

Комбинаторика посвящена решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными свойствами. Комбинаторика занимается изучением числа всех возможных способов размещения некоторых предметов конечного множества, или числа всех возможных способов выполнения определенного действия из конечного множества таких действий.

Рассмотрим первое основное правило комбинаторики или правило произведения.

Пусть необходимо выполнить работу, совершая последовательно k действий. Определим количество способов N выполнения работы. Если первое действие можно выполнить способами, второе способами и так далее, причем последнее k-тое действие можно выполнить способами, то все k действий можно выполнить способами, т.е.

N= .

Другим часто применяемым в комбинаторике правилом является правило суммы. Это правило формулируется следующим образом: если элемент может быть выбран способами, а элемент — способами, и т.д., то количество N вариантов выбора «либо , либо , …,либо » равно

N= .

Перечислительная комбинаторика или теория перечислений изучает числа способов построения кортежей из элементов конечного множества. Простейшими такими кортежами являются размещения, перестановки, сочетания.

Пусть А — конечное множество, состоящее из п элементов.

Размещениями из п элементов множества А по k называются кортежи длины k, состоящие из различных элементов n-элементного множества А, отличающиеся один от другого как самими элементами, так и их порядком. Число таких размещений обозначается (буква А от французского слова arrangement — размещение). Размещениям соответствует схема выбора k элементов из n-элементного множества без возвращения. При этом необходимо совершить k действий, причем первое действие можно совершить п способами, второе способами и т. д., k-e действие способами. Согласно комбинаторному правилу умножения, получим формулу: .

Если умножить и разделить полученное выражение на получим:

где называется факториалом числа п (читается n-факториал). Отметим, что и т.д.

Пример 2.1. Для множества выпишем все размещения из трех элементов по два: .

Число размещений определяется по формуле

.

Перестановками из элементов множества А называются кортежи длины , состоящие из различных элементов n-элементного множества А. Эти кортежи будут отличаться друг от друга только порядком следования элементов, поскольку в каждом из них встречаются по одному разу все элементы множества А. Перестановки обозначаются (от английского слова permutation— перестановка). Поскольку , то число перестановок вычисляется по формуле .

Пример 2.2. Для множества выпишем все возможные перестановки из трех элементов: .

Число перестановок определяется по формуле

Сочетаниями из п элементов множества А по k называются кортежи длины k, состоящие из различных элементов n-элементного множества А, отличающиеся только самими элементами, а не их порядком следования. Сочетаниями обозначаются (буква С от английского слова combination — комбинация).

Число сочетаний по k меньше числа размещений из п элементов по k в раз, т. е.

.

Таким образом, имеем

.

Из этой формулы непосредственно вытекает, что , , .

Пример 2.3. Для множества выпишем все сочетания из трех элементов по два: .

Число сочетаний определяется по формуле

.

Непосредственной проверкой легко доказать следующие тождества:

a) , где .

Действительно:

.

б) .

Данное тождество доказывается аналогичным образом:

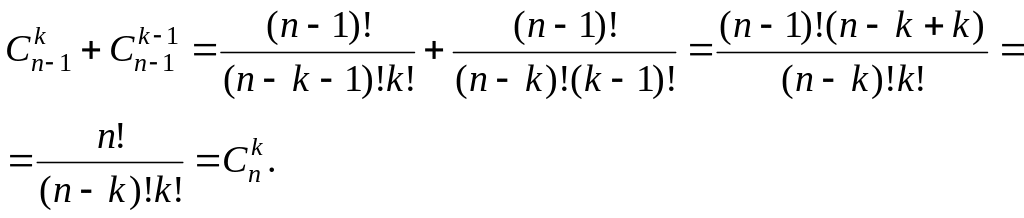
С числами связано функциональное тождество, называемое формулой бинома Ньютона. Известные из элементарной математики формулы сокращенного умножения:

можно переписать с использованием сочетаний так:

.

В общем случае справедливо тождество, известное как биномом Ньютона:

,

Где коэффициенты называются биномиальными коэффициентами.

Если положить то из формулы бинома Ньютона вытекает соотношение: — формула суммы биномиальных коэффициентов.

Если положить в биноме Ньютона , то

.

Поскольку , то биномиальные коэффициенты, равноотстоящие от концов в формуле бинома Ньютона, равны.

Все приведенные формулы для размещений, сочетаний и перестановок справедливы в том случае, когда п элементов множества А различны. Если же некоторые элементы повторяются, то в этом случае рассматриваются комбинации с повторениями, число которых вычисляется по другим формулам.

Размещениями с повторениями из п элементов по k называются кортежи длины k, составленные из п — элементного множества А. Число этих кортежей обозначают и равно

Черта указывает на возможность повторения элементов в размещении.

Пример 2.4. Для множества вычислим количество размещений с повторениями, т.е. определим, сколько пятизначных номеров можно составить из элементов множества ? Такими номерами являются кортежи длины 5, составленные из семиэлементного множества, где схема выбора состоит в выборе 5 элементов из семиэлементного множества с возвращением, т.е. для каждого из пяти элементов есть семь способов выбора, т. е. .

Перестановкой с повторениями состава из элементов называют любой кортеж длины , в который входит раз, входит раз, ..., раз. Число таких перестановок обозначают

.

Пример 2.5. Сколько вариантов слов можно получить, переставляя буквы в слове «математика»? Слово «математика» является кортежем длины 10, имеющем состав (2, 3, 2,1,1,1) (буква «м» входит два раза, буква «а» входит 3 раза, буква «т» входит два раза, буквы «е», «и», «к» входят по одному разу). Таким образом, число вариантов, возникающих при перестановках букв, равно

.

Рассмотрим сочетания с повторениями. Пусть имеются предметы п видов и из них составляется набор, содержащий k элементов, т. е. различными исходами будут всевозможные наборы длины k, отличающиеся составом, и при этом отдельные наборы могут содержать повторяющиеся элементы. Такие наборы называются сочетаниями с повторениями, а их общее число определяется формулой:

.

Пример 2.6. Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4 сорта?

Искомое число равно .