
- •Операции над комплексными числами.
- •2.1. Условие дифференцируемости функции комплексной переменной
- •2.2. Геометрический смысл аргумента и модуля производной
- •2.3. Гармонические функции
- •3. Элементарные функции комплексной переменной (кп)
- •3.1. Дробно-линейная функция
- •3. Рассмотрим общее дробно-линейное преобразование
- •3.3. Показательная функция и логарифм
- •4.Разложение функции комплексной переменной в ряды тейлора и лорана
- •4.1. Сходимость и равномерная сходимость
- •4.2. Свойства равномерно сходящихся рядов
- •4.3. Область сходимости степенного ряда
- •4.4. Ряд Тейлора
- •4.5. Способы разложения функций в ряд Тейлора
- •4.6. Ряд Лорана, разложение функций в ряд Лорана.
- •5. Вычеты и их приложения
- •Библиографический список
- •394026 Воронеж, Московский просп., 14
3.3. Показательная функция и логарифм
Показательная
функция определяется
для любого комплексного
![]() соотношением
соотношением
![]()
![]()
![]() (21)
(21)
Из
этого определения вытекают следующие
свойства
![]() :
:
1.
Для действительных чисел
![]() получаем показательную функцию
действительного переменного
получаем показательную функцию
действительного переменного
![]() .
.
2. Функция всюду аналитична и ее производная вычисляется по формуле
![]() .
.
Выполнение условий Даламбера-Эйлера проверяется элементарно. Используя факт независимости производной от направления, по которому происходит стремление текущей точки к предельной, возьмем производную по направлению, параллельному оси Оx:
![]() .
.![]()
3. Сохраняется основное свойство показательной функции (в области действительного переменного), выражаемое теоремой сложения
![]()
![]()
![]()
![]()
4. Показательная функция не обращается в нуль ни при каких значениях показателя, так как
![]() .
.
Полагая
в (21)
![]() ,
,
![]() ,
получим формулу
Эйлера:
,
получим формулу
Эйлера:
![]() (23)
(23)
С помощью формулы Эйлера любое комплексное число можно записать в показательной форме
![]() (24)
(24)
5.
Показательная функция является
периодической с периодом![]() ,
так как
,
так как
![]() .
В силу свойства периодичности изучение
функции
.
В силу свойства периодичности изучение
функции
![]() сводится к изучению ее свойств в полосе
шириной
и параллельной оси Оx, например в полосе
сводится к изучению ее свойств в полосе
шириной
и параллельной оси Оx, например в полосе
![]() /вообще
говоря, в одной
из полос
/вообще
говоря, в одной
из полос
![]() /.
/.
Действительно,
![]() силу
периодичности. Отсюда,
силу
периодичности. Отсюда,
![]() .
.
Значит отображение, определяемое функцией , однолистно в указанных полосах.
Введем
в плоскости W
полярные координаты
![]() .
Тогда
.
Тогда
![]() по формуле Эйлера. Из (21)
по формуле Эйлера. Из (21)
![]()
Отсюда
следует, что прямые
![]() ,
,
![]() (в
плоскости z ) отображаются в окружности
радиуса
(в
плоскости z ) отображаются в окружности
радиуса
![]() и
лучи
и
лучи
![]() соответственно,
рис. 10
соответственно,
рис. 10
y0=φ
2π
x
y
G
F(X= -∞)
D
E
C
B
A
0
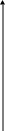





![]()

E’
B’
D’
A’
F’
G’
v
0’o’
C’







Рис. 10.
При
этом ось Оx (![]() )
и прямая
)
и прямая
![]() преобразуются в лучи
и
.
Чтобы соблюсти взаимную однозначность
отображения, на плоскости w производим
разрез по полуоси и
.
Тогда Оx переходит в верхний
берег разреза,
а
-
в нижний
берег.
преобразуются в лучи
и
.
Чтобы соблюсти взаимную однозначность
отображения, на плоскости w производим
разрез по полуоси и
.
Тогда Оx переходит в верхний
берег разреза,
а
-
в нижний
берег.
Таким
образом, функция
![]() отображает
каждую
горизонтальную полосу плоскости z
шириной
на плоскость с разрезом по полуоси
отображает
каждую
горизонтальную полосу плоскости z
шириной
на плоскость с разрезом по полуоси
![]() .
Вся плоскость Z
при этом отображается в бесконечнолистную
плоскость w .
.
Вся плоскость Z
при этом отображается в бесконечнолистную
плоскость w .
Логарифмическая
функция определяется как функция,
обратная к показательной; число W
называется логарифмом числа z, если
![]() и обозначается
и обозначается
![]() .
.
Из определения логарифмической функции и свойств показательной функции получим основные свойства логарифмов от комплексных чисел.
I.Пусть
![]()
![]()
![]() (25)
(25)
(25) - есть обобщение известного из элементарной математики свойства логарифма.
2.
Пусть
![]() .
Тогда по формуле (25)
.
Тогда по формуле (25)
![]()
В
этой формуле, так как
![]() - действительное положительное число,
в первом слагаемом использовано обычное
обозначение натурального логарифма.
- действительное положительное число,
в первом слагаемом использовано обычное
обозначение натурального логарифма.
Как
известно
![]() - бесконечнозначная функция, поэтому
любое комплексное число имеет бесконечное
множество значений логарифма:
- бесконечнозначная функция, поэтому
любое комплексное число имеет бесконечное
множество значений логарифма:
![]() (26)
(26)
В этой формуле - главное значение аргумента комплексного числа.
Условимся
через
![]() обозначать главное
значение бесконечнозначной функции
соответствующее
обозначать главное
значение бесконечнозначной функции
соответствующее
![]() :
:
![]() ,
,
Значение зависит от того, какое значение выбрано для
Рис.11.
аргумента комплексного числа.
Рассмотрим в плоскости Z две кривые C и L , рис. 11.
y
x
Ĺ
A
Z0
C
W=Lnz
Z
x
y
W
Č1
Č
w0
Ļ










Пусть
точка
![]() пробегает
кривую С от начального положения
.
Выберем для значений аргументов точек
главные их значения. При возвращении в
точку
значение аргумента, которое менялось
от точки к точке при прохождении кривой
С
, останется прежним -
.
пробегает
кривую С от начального положения
.
Выберем для значений аргументов точек
главные их значения. При возвращении в
точку
значение аргумента, которое менялось
от точки к точке при прохождении кривой
С
, останется прежним -
.
Соответствующая
точка в плоскости w также опишет замкнутую
кривую Ć
и вернется в прежнюю точку
![]() .
.
При
выборе в качестве аргументов z значений
![]()
![]() точки в плоскости W
будут описывать кривые
точки в плоскости W
будут описывать кривые![]() ,
которые получаются из
,
которые получаются из
![]() смещением на
смещением на
![]() по оси
по оси
![]() .
Таких кривых
будет бесконечно много.
Они
дадут бесконечно много отделенных
друг от друга ветвей функции
.
Таких кривых
будет бесконечно много.
Они
дадут бесконечно много отделенных
друг от друга ветвей функции
![]() .
.
Если
кривая L
в, плоскости Z
содержит внутри
своего контура точку
,
то при каждом
обходе по замкнутому контуру L
аргументы соответствующих точек z
возрастают на
,
поскольку радиус-вектор поворачивается
на угол
при возвращении в точку z. Следовательно,
соответствующая точка
![]() будет описывать незамкнутую кривую
будет описывать незамкнутую кривую
![]() ,
ибо у функции
,
ибо у функции
мнимая часть изменится на при каждом возвращении точки z в прежнее положение .
В этом случае говорят, что ветви функции отделить нельзя: они непрерывно переходят одна в другую. Таким образом, если область не содержит кривых, обходящих начало координат , ветви отделяются и каждая из них осуществляет взаимно-однозначное отображение области D.
Следовательно, по теореме о производной обратной функции
![]() (27)
(27)
3.4. Тригонометрические и гиперболические функции
По формуле Эйлера (23) имеем
![]() (28).
(28).
Формулы (28) дают выражение тригонометрических функций действительного переменного через показательную функцию.
Примем по определению для любого комплексного числа z
![]() (29)
(29)
Определенные
функции
![]() и
и
![]() являются линейными комбинациями
показательных функций переменного
являются линейными комбинациями
показательных функций переменного
![]() ,
поэтому свойства тригонометрических
функций, в основном, обусловлены
свойствами показательной функции.
,
поэтому свойства тригонометрических
функций, в основном, обусловлены
свойствами показательной функции.
1.
Для действительных
![]() и
и
![]() совпадают с соответствующими функциями
совпадают с соответствующими функциями
![]() и
и
![]() .
.
2. sinz и cosz всюду аналитичны, так как всюду аналитична показательная функция.
3. sinz и подчиняются обычным (из анализа действительной переменной) формулам дифференцирования:
![]() (30
(30
4.
и
периодичны с периодом
![]() .
Вследствие периодичности показательной
функции
.
Вследствие периодичности показательной
функции
![]() .
.
![]()
Аналогично
![]() .
.
С помощью несложных выкладок можно убедиться, что выполняются обычные тригонометрические тождества
![]() и
т.д.
и
т.д.
Поскольку
периодом функций
и
является действительное
число
,
областями однолистности соответствующих
отображений будут вертикальные полосы
![]() ,
так как, например,
,
так как, например,
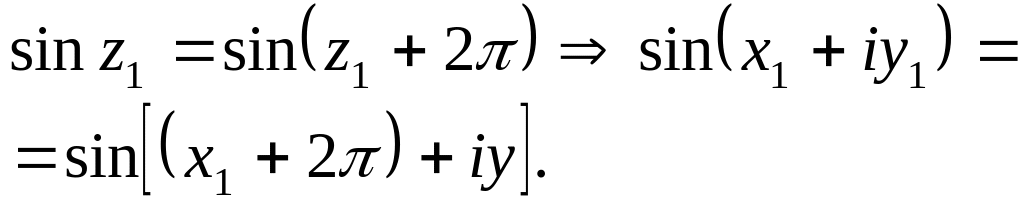
5.
Тригонометрические функции в комплексной
плоскости обладают новым, по сравнению
с теми же функциями действительного
переменного, свойством:
их модули
бесконечно возрастают при стремлении
![]() вдоль оси Оy, т.е. при
вдоль оси Оy, т.е. при
![]() .
.
Действительно
![]()
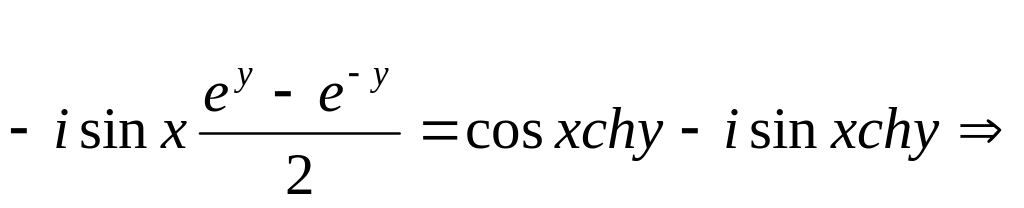
![]()
Отсюда
видно, что
![]() является
периодической по
x
функцией (при фиксированном y
) и
является
периодической по
x
функцией (при фиксированном y
) и
![]() .
.
Гиперболические
функции комплексного переменного
![]() и
и
![]() - определяются по аналогии с соответствующими
функциями действительного переменного:
- определяются по аналогии с соответствующими
функциями действительного переменного:
![]() (31)
(31)
Эти функции в силу определения выражаются через тригонометрические по формулам
![]() (32)
(32)
Гиперболические
функции вместе с показательной являются
периодическими,
![]() ,
и всюду аналитическими:
,
и всюду аналитическими:
![]() .
.
Функции тангенса и котангенса определяются обычными формулами:
![]() .
.
