5.2.1. Основы надежности механической системы и её элементов

Рассмотрим следующую модель эксплуатации восстанавливаемых элементов. В некоторый момент времени, принятый за начальный, элемент начинает работать и, проработав случайное время τ₁ ,выходит из строя. После отказа происходит восстановление и элемент вновь работает до отказа время τ₂. Этот процесс продолжается неограниченно. При этом время восстановления не учитывается. Предполагается, что случайные времена τ_1, τ_2,…. τ_n имеют один и тот же закон распределения . Кроме того, они могут быть охарактеризованы плотностью распределения f(t), средним значением наработки до отказа T₀ и её дисперсией D₀.

Моменты отказов (рис. 5.2) t=τ₁, t₂=τ₁+τ₂,…, t_n=τ₁+τ₂+…+τ_n образуют случайный поток, который называют потоком отказов.

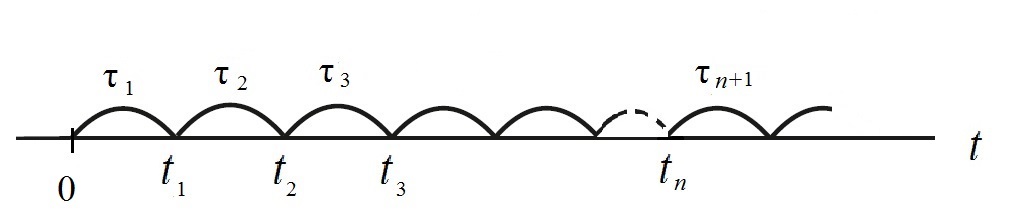
Рис. 5.2. Поток отказов элемента

Важнейшим показателем потока отказов элемента является ведущая функция Ω(t) (функциям восстановления), равная среднему числу отказов элементов m(t), происходящих за время t. В свою очередь, имеет место равенство

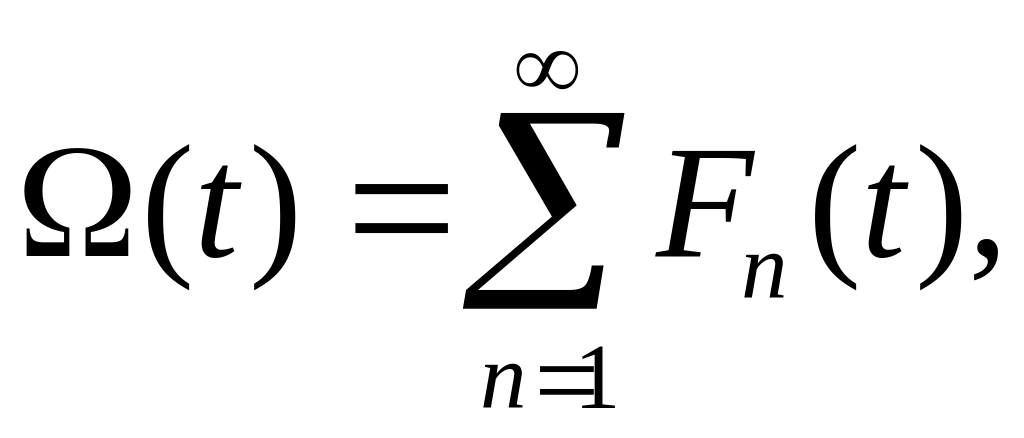(5.1)

где – законы распределения t_n .

Статистическая оценка

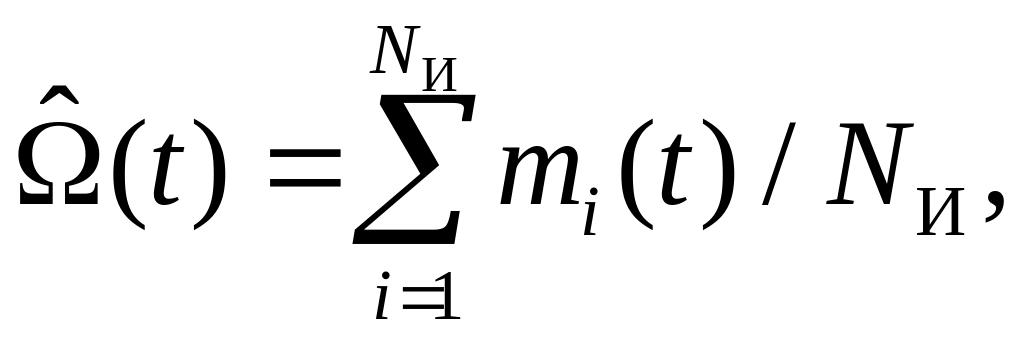(5.2)

где m_i(t) – число отказов i-го из наблюдаемых N_и элементов за время t.

Статистическая оценка средней наработки элемента до отказа будет равна

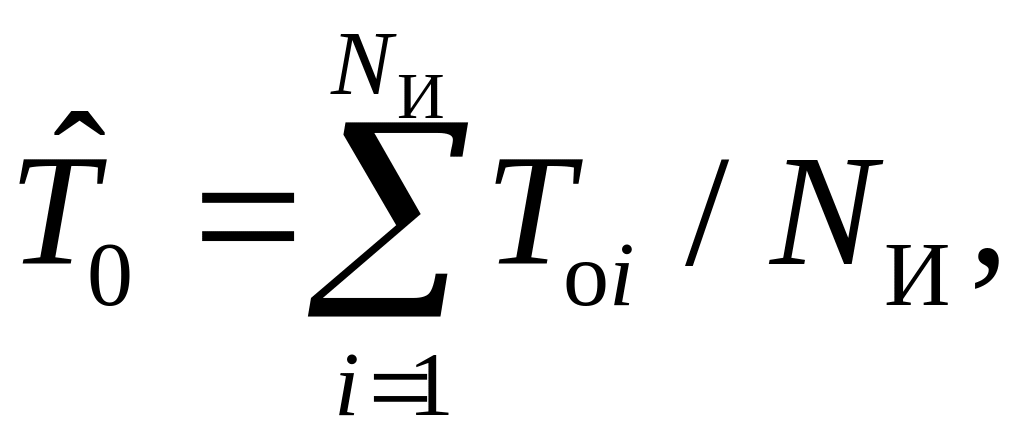(5.3)

где T_oi – длительность наработки до отказа i-го из наблюдаемых N_И элементов.

Другой важнейшей характеристикой надёжности восстанавливаемых элементов является интенсивность потоков отказов:

(5.4)

Соответственно

(5.5)

где

Статистическая оценка :

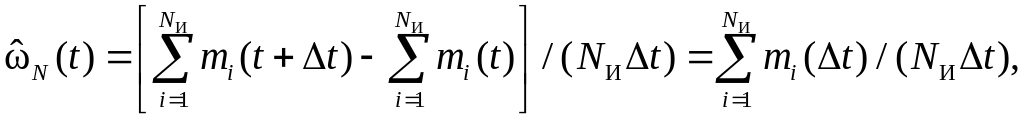(5.6)

где – число отказов i - го из наблюдаемых N_И элементов в интервале времени ∆t.

Для ординарных потоков отказов без последствия интенсивность потока совпадает с параметром потока. В этом случае показатель «параметр потока отказов» связан с ведущей функцией соотношением

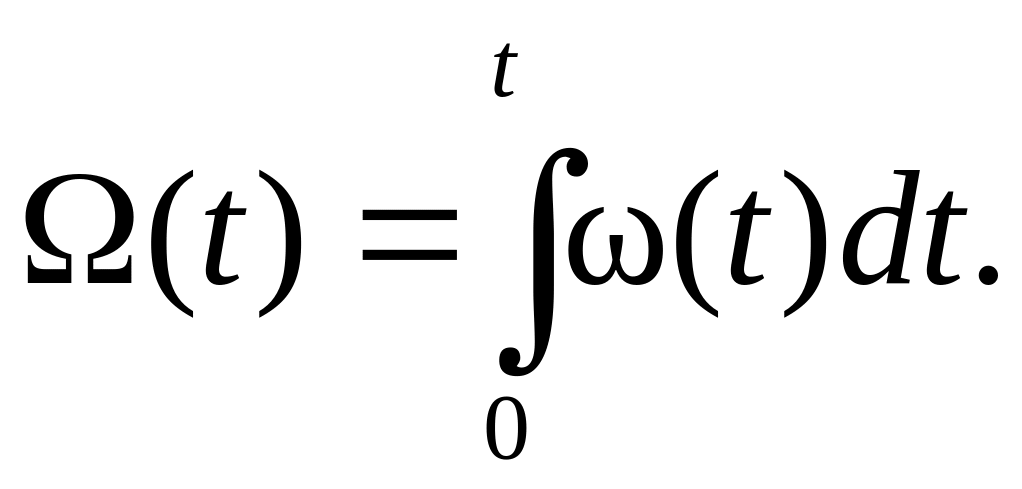(5.7)

Рассмотрим некоторые свойства потока отказов:

1) для большого периода времени среднее число отказов, приходящихся на единицу времени, близко к величине, обратной наработке элемента до отказа:

; (5.8)

2) для большого периода времени может быть использована приближенная зависимость

; (5.9)

3) с течением времени процесс восстановления становится стационарным и его локальные характеристики представляют зависимость от времени

(5.10)

При значительном времени восстановления модель (см. рис. 5.2) преобразуется в модели на рис. 5.3.

Рис. 5.3. Поток отказов элемента с конечным временем восстановления

Элемент, проработав случайное время , выходит из строя и восстанавливается в течение случайного времени ; восстановленный элемент работает время и восстанавливается за время и т.д.

Предполагают, что случайные величины наработки и восстановление независимы.

Процесс, описываемый данный моделью, называют потоком отказов (процессом восстановления) с конечным временем восстановления. Статистическая оценка среднего времени восстановления

(5.11)

где – длительность восстановления i - го из наблюдаемых N_И элементов.

Особой характеристикой рассматриваемого процесса является коэффициент готовности К_Г , который равен вероятности того, что элемент окажется работоспособным в произвольный момент времени, кроме планируемых периодов, в течение которых использование элемента по назначению не предусматривается.

Коэффициент готовности

(5.12)

Коэффициент готовности статистически определяется отношением суммарного времени наблюдаемых элементов в работоспособном состоянии к произведению числа этих элементов на продолжительность эксплуатации (за исключением простоев на проведение плановых ремонтов и технического обслуживания):

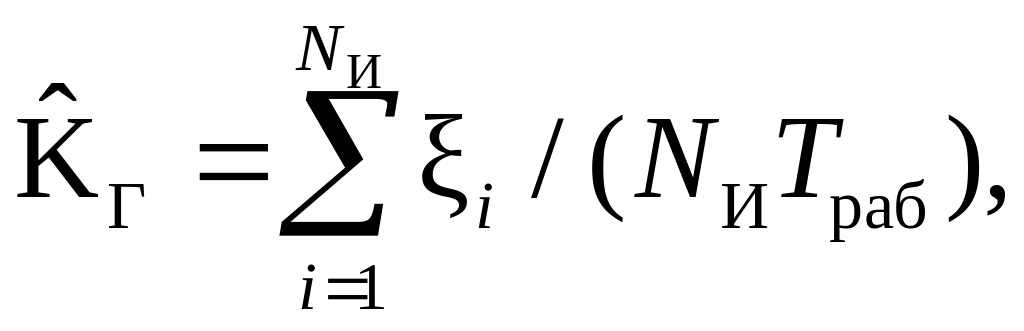(5.13)

где – суммарное время пребывания i-го элемента в работоспособном состоянии (i=1,2… N_И); – продолжительности эксплуатации элементов, состоящих из последовательно чередующихся интервалов времени работы и восстановления.

Рассмотренные выше понятия, полученные с помощью методов теории вероятности и математической статистики, характеризуют свойства безотказности и ремонтопригодности восстанавливаемых элементов.

В том случае, когда требуется оценить взаимосвязь надёжности отдельных частей объекта, его представляют в виде системы, состоящей из отдельных элементов (см. рис. 5.1). Предполагается, что элементы отказывают независимо друг от друга, т.е. отказ любого из элементов не изменяет надёжность других элементов.

Рассмотрим первоначально надёжность системы с независимыми элементами, работающей до первого отказа. При ситуации, когда отказ любого из элементов вызывает отказ всей системы, считают, что элементы соединены последовательно в смысле надёжности (рис. 5.4).

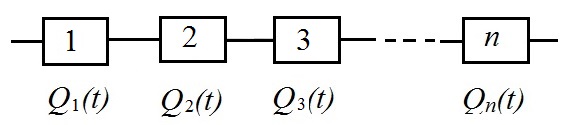
Рис. 5.4. Последовательное соединение элементов в систему

Следует отметить, что в механических системах наблюдается большей частью последовательное соединение элементов.

Тогда вероятность безотказной работы системы в пределах заданной наработки определяется следующим образом:

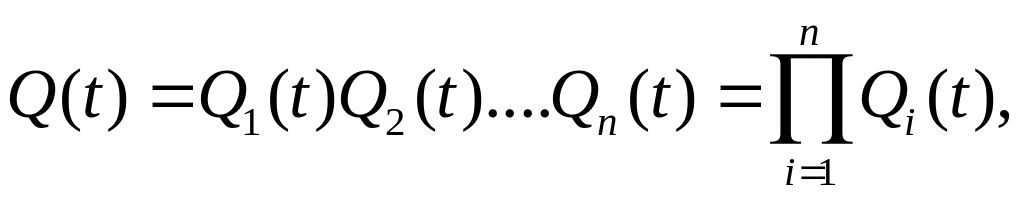(5.14)

где – вероятность безотказно работы i-го элемента за время наработки t.

В том случае, когда распределение отказов элементов подчиняется экспоненциальному закону, закон распределения отказов системы также подчиняется экспоненциальному закону с параметром :

(5.15)

где – интенсивность отказов i-го элемента.

Если обозначить в этом случае через среднюю наработку до отказа системы, а через – среднюю наработку до отказа i-го элемента, то

(5.16)

так как для экспоненциального закона

Рассмотрим надежность восстанавливаемой системы с последовательным соединением (в смысле надёжности) элементов. Предположим, что каждый элемент системы после отказа восстанавливается мгновенно. Причём исходные свойства элемента восстанавливаются полностью. Моменты отказов каждого элемента образуют поток отказов (процесс восстановления), причём в силу таких предположений эти потоки являются независимыми.

Обозначим черезF_k(t) (k=1,2,…,n) закон распределения наработки до отказа k-го элемента. Предполагается, что эти законы имеют непрерывную плотность f_k и существует наработка до отказа T_ok и его дисперсия D_ok.

Если моменты отказов всех элементов отметить на общей оси времени, то получим поток отказов системы. Этот поток есть сумма потоков отказов элементов (рис. 5.5).

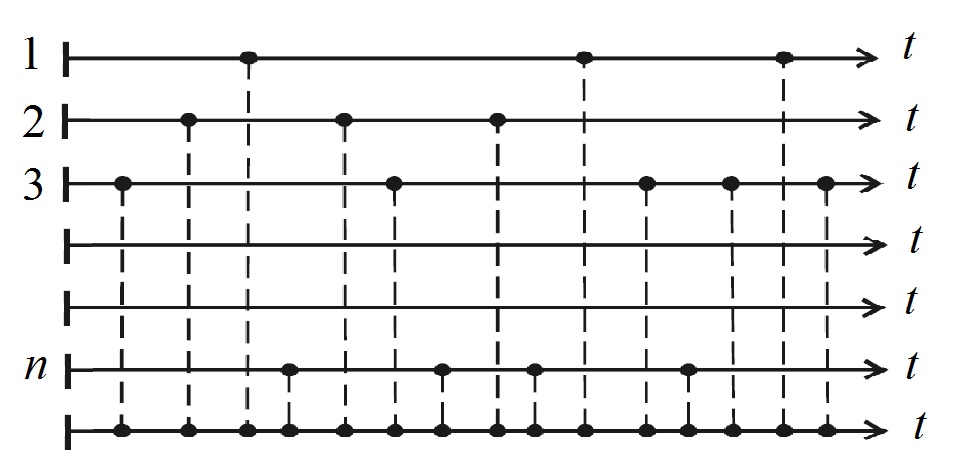
Рис. 5.5. Потоки отказов

Среднее число отказов системы до момента времени t определится как

(5.17)

Интенсивность потока отказов системы определится как

(5.18)

Для ординарных потоков отказов элементов без последействия интенсивность потока системы совпадает с параметром потока .

Ординарность – невозможность появления двух или нескольких событий за малый промежуток времени. Отсутствие последствия – отсутствие влияния предшествующих событий.

В связи с тем, что интенсивность потока отказов каждого элемента стремится к пределу

(5.19)

интенсивность потока отказов системы имеет предел

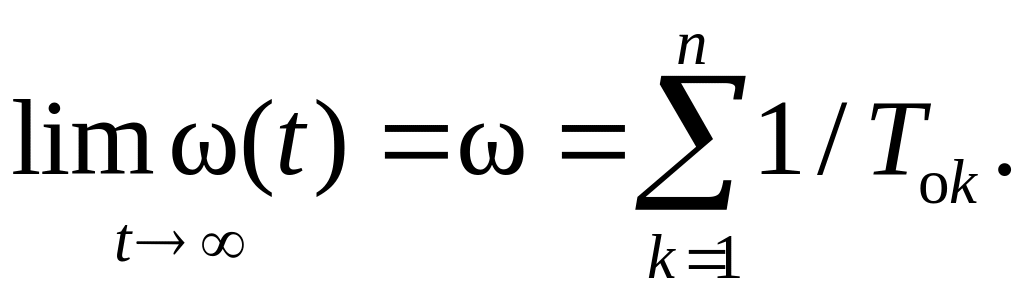(5.20)

В частном случае, если наработка до отказа каждого элемента подчиняется экспоненциальному закону (интенсивность отказов элемента ), то поток отказов для каждого элемента образует простейший поток и, значит, поток отказов системы как сумма простейших потоков также будет простейшим с интенсивностью

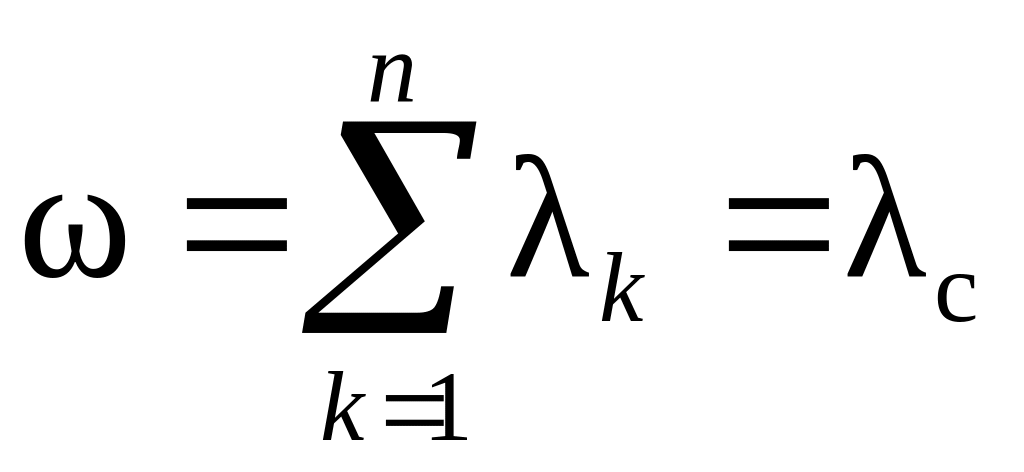. (5.21)

Перейдём к рассмотрению надёжности системы с конечным временем восстановления каждого элемента. При этом предполагаем, что во время восстановления одного элемента все другие элементы продолжают работать. Известно, что F_k(t) – закон распределения наработки до отказа k-го элемента, а L_k(t) – закон распределения времени его восстановления. Существует также T_ok и T_вk, а также дисперсии D_ok и D_вk .

В простейшем случае можно предположить, что на рассматриваемом участке времени интенсивность потоков отказов элементов и системы изменяются незначительно. Тогда периоды работы системы ( ) распределяются по экспоненциальному закону

(5.22)

а периоды восстановления ( ) имеют распределение

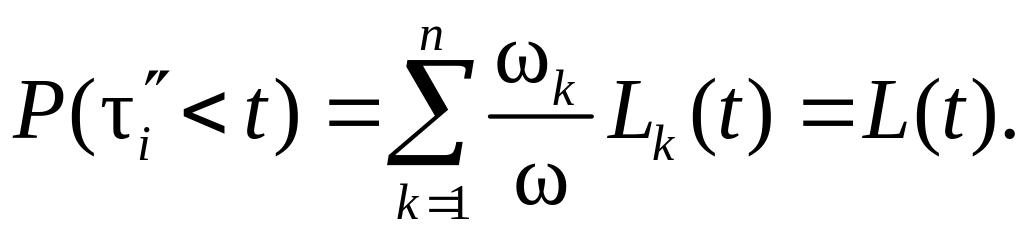(5.23)

Наработка до отказа системы

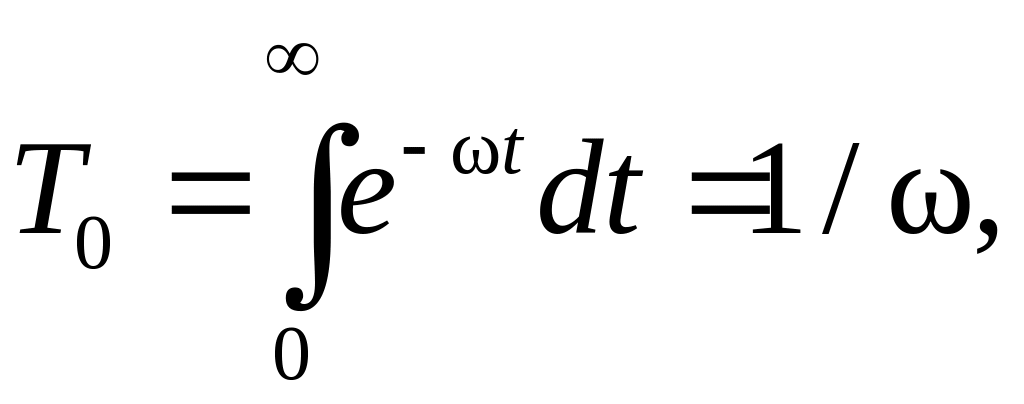(5.24)

а среднее время восстановления системы

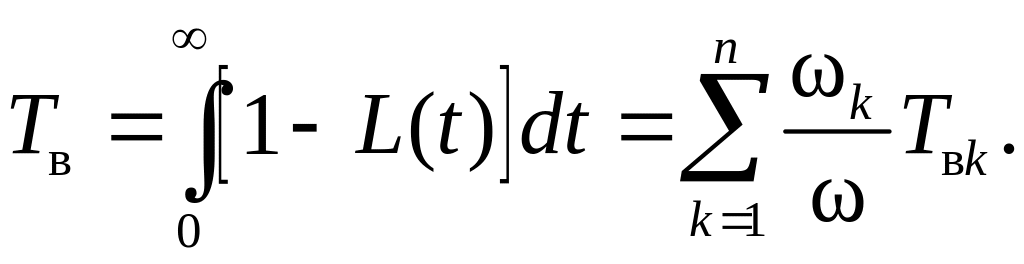(5.25)

Соответственно коэффициент готовности на заданном участке наработки определяется как

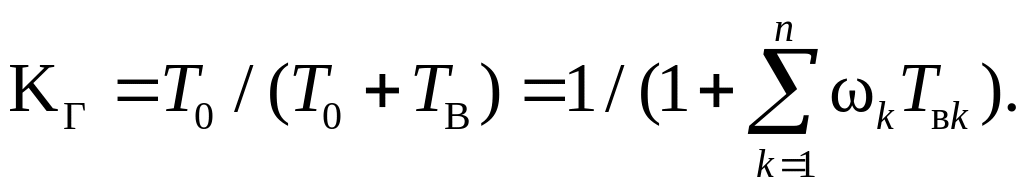(5.26)

Если система работает достаточно долго, то интенсивности и приближаются к своим пределам (выражения (5.9) и (5.10)).

Соответственно

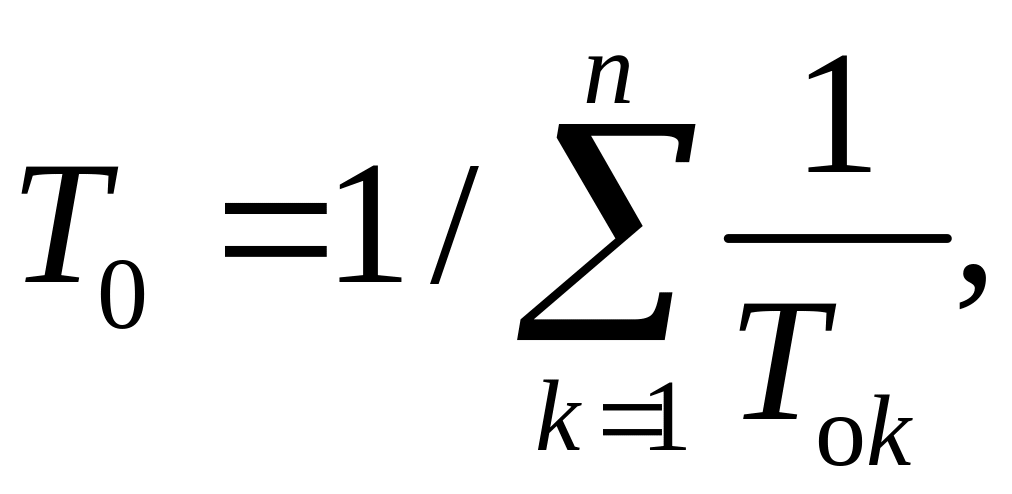(5.27)

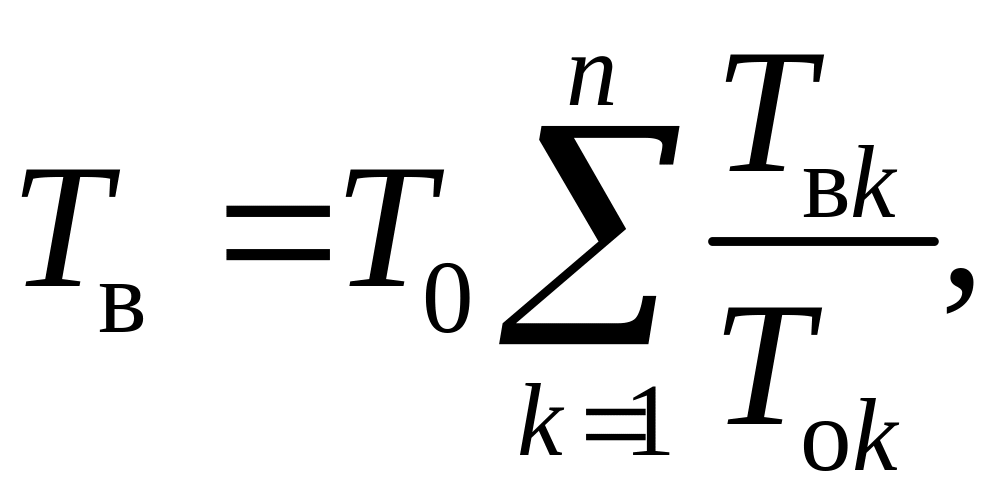(5.28)

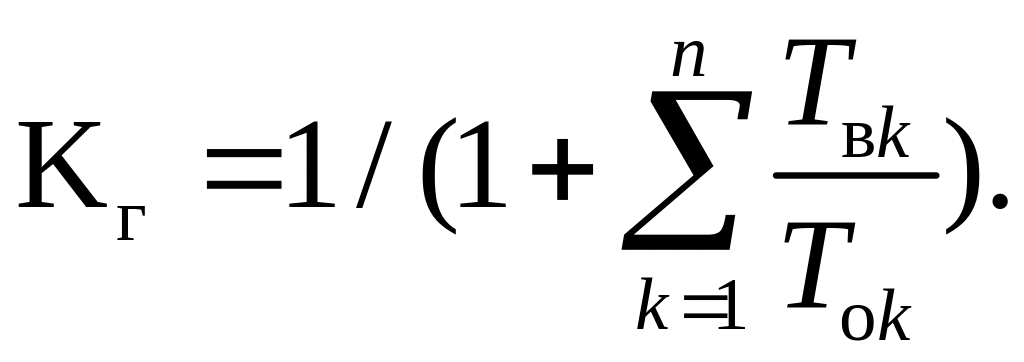(5.29)