
- •Введение
- •1. Вводные сведения
- •1.1. Предмет механики жидкости и газа
- •1.2. Краткие исторические сведения о развитии науки
- •2. Основные физические свойства жидкостей и газов
- •2.1. Физическое строение жидкостей и газов
- •2.2. Основные физические свойства: сжимаемость, текучесть, вязкость, теплоемкость, теплопроводность
- •2.3. Гипотеза сплошности
- •2.4. Два режима движения жидкостей и газов
- •2.5. Неньютоновские жидкости
- •2.6. Термические уравнения состояния
- •2.7. Растворимости газов в жидкостях, кипение, кавитация. Смеси.
- •2.8. Законы переноса
- •2.9. Требования к рабочим жидкостям
- •3. Основы кинематики сплошных сред
- •3.1. Два метода описания движения жидкостей и газов
- •3.2. Понятие о линиях и трубках тока. Ускорение жидкой частицы
- •3.3. Расход элементарной струйки и расход через поверхность
- •3.4. Уравнение неразрывности (сплошности)
- •3.5. Вихревое и безвихревое (потенциальное) движения
- •4. Силы, действующие в жидкостях
- •4.1. Массовые и поверхностные силы
- •4.2. Напряжения поверхностных сил
- •4.3. Напряженное состояние
- •5. Общие законы и уравнения статики и динамики жидкостей и газов
- •5.1. Уравнения движения в напряжениях
- •5.2. Уравнения гидростатики в форме Эйлера и их интегралы
- •5.3. Напряжения сил вязкости, обобщенная гипотеза Ньютона
- •5.4. Уравнение Навье-Стокса для вязкой жидкости
- •5.5. Примеры аналитических решений уравнений Навье-Стокса для ламинарного движения в цилиндрических трубах
- •6. Абсолютный и относительный покой (равновесие) жидких сред
- •6.1. Основная формула гидростатики
- •6.2. Определение сил давления покоящейся среды на плоские и криволинейные стенки
- •6.3. Относительный покой (равновесие) жидкости
- •Следовательно, вместо уравнения (6.5) можно записать:
- •7. Модель идеальной (невязкой) жидкости
- •7.1. Модель идеальной (невязкой) жидкости. Уравнения Эйлера
- •7.2. Интегралы уравнения движения жидкости для разных случаев движения. Баротропные и бароклинные течения
- •8. Общая интегральная форма уравнений количества движения и момента количества движения
- •8.1. Законы сохранения
- •8.2. Закон изменения количества движения
- •8.3. Закон изменения момента количества движения
- •8.4. Силовое воздействие потока на ограничивающие его стенки
- •9. Общее уравнение энергии в интегральной и дифференциальной формах
- •10. Турбулентность и ее основные статистические характеристики
- •10.1. Турбулентное течение
- •10.2. Осредненные параметры и пульсации. Стандарт пульсационной скорости и степень турбулентности
- •10.3. Двухслойная модель турбулентности
- •11. Подобие гидромеханических процессов
- •11.1. Числа и критерии подобия
- •11.2. Понятие о методе размерностей. Пи-теорема
- •11.3. Методы моделирования
- •11.4. Методы аналогий
- •12. Одномерные потоки жидкостей и газов
- •12.1. Уравнение д. Бернулли для струйки и потока реальной (вязкой) жидкости
- •12.2. Гидравлические потери (общие сведения)
- •13. Ламинарное течение в круглых трубах
- •13.1. Течение при больших перепадах давления
- •13.2. Ламинарное течение с облитерацией
- •13.3. Ламинарное течение с теплообменом
- •14. Потери напора при турбулентном течении в гидравлически гладких круглых трубах
- •14.1. Потери напора при турбулентном течении в шероховатых трубах. График и.И. Никурадзе
- •15. Местные гидравлические сопротивления
- •15.1. Внезапное расширение русла
- •15.2. Внезапное сужение русла
- •15.3. Местные сопротивления при ламинарном течении
- •16. Истечение жидкости через отверстие в тонкой стенке при постоянном напоре
- •16.1. Истечение через насадки при постоянном напоре
- •17. Истечение через отверстия и насадки при переменном напоре
- •17.1. Неустановившееся движение жидкости в трубах
- •17.2. Гидравлический удар
- •18. Расчет простых трубопроводов
- •18.1. Основные задачи по расчету простых трубопроводов
- •18.2. Последовательное соединение простых трубопроводов
- •18.3. Параллельное соединение простых трубопроводов
- •18.4. Разветвлённое соединение простых трубопроводов
- •19. Расчет сложных трубопроводов
- •19.1. Трубопроводы с насосной подачей жидкости
- •19.2. Основы расчета газопроводов
- •Заключение
- •Библиографический список
- •Оглавление
- •Гоувпо «Воронежский государственный технический университет»
- •394026 Воронеж, Московский просп., 14
6.2. Определение сил давления покоящейся среды на плоские и криволинейные стенки
В общем случае на поверхность s, погруженную в жидкость, будет действовать совокупность сил гидростатического давления, которая в соответствии с законами статики твердого тела может быть приведена к одной силе, равной главному вектору сил давления
![]() ,
,
и к одной паре с моментом, равным
![]() .
.
Найдем величину главного вектора, приложенного к некоторой криволинейной поверхности (рис. 6.3), погруженной в жидкость.
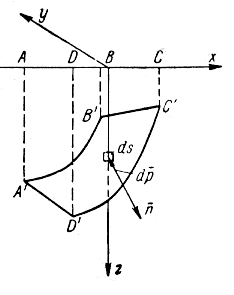
Рис. 6.3. Схема сил, воздействующих
на криволинейную поверхность
Вначале рассмотрим
элементарную силу
![]() ,
действующую на площадку ds.
Очевидно, сила
будет направлена по нормали к площадке
ds
и равна
,
действующую на площадку ds.
Очевидно, сила
будет направлена по нормали к площадке
ds
и равна
![]() .
.
Проекции этой силы на оси х, у и z (рис. 6.3) представляют собой горизонтальные и вертикальную составляющие, величины которых соответственно равны
![]() ;
;
![]() ;
;
![]() .
.
так как проекциями орта нормали на оси координат являются косинусы углов между нормалью и соответствующей осью координат.
Из рис. 6.3 видно, что
![]() ;
(6.8)
;
(6.8)
Тогда составляющие силы давления, действующей на площадку ds, можно представить в виде
![]() ;
;
![]() ;
;
![]() .
.
Если воспользоваться формулой (6.7) и пренебречь атмосферным давлением, то последние зависимости примут вид
![]() ;
;
![]() ;
;
![]() .
.
Напомним, что индекс у буквы s означает проекцию площадки ds на плоскость, перпендикулярную соответствующей оси.
Компоненты сил давления на всю рассматриваемую криволинейную поверхность, погруженную в жидкость, будут равны
![]() (6.9)
(6.9)
где U - объем жидкости, заключенный между рассматриваемой криволинейной поверхностью и поверхностью жидкости.
На рис. 6.3 этот объем ограничен поверхностью AA'BB'CC'. Таким образом, вертикальная составляющая суммарного давления жидкости на криволинейную стенку равняется весу жидкости в объеме цилиндрической поверхности с вертикальными образующими, ограниченной снизу криволинейной стенкой и сверху поверхностью жидкости.
Горизонтальные составляющие суммарной силы давления на криволинейную стенку, как видно из формул, тоже определяются через веса некоторых объемов.
Главный вектор сил давления на стенку по величине равен
![]() .
.
Точка приложения главного вектора, называемая центром давления, определяется для криволинейной стенки довольно сложно.
Найдем главный вектор и центр давления для плоской стенки s, расположенной под некоторым углом к горизонту (рис. 6.4).
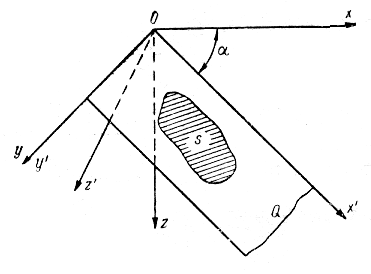
Рис. 6.4. Главный вектор и центр давления
для плоской стенки
Для этого проведем плоскость Q, включающую стенку s, до ее пересечения с поверхностью жидкости и расположим две системы координат, имеющих общее начало в точке О, так, чтобы плоскость хОу одной системы лежала на поверхности жидкости, а плоскость системы x'Oy' совпадала с плоскостью Q. Если оси у и у' совместим с прямой, образованной от пересечения плоскости Q с поверхностью жидкости, то угол между осями х и x' будет равен углу наклона плоскости стенки. Ось z' будет нормалью к Q и s. Тогда в соответствии с выражениями (6.8) получим
![]() ;
;
![]() ;
;
![]() .
.
Откуда величина главного вектора будет равна
![]() .
.
Последний интеграл
равен площади стенки s,
умноженной на координату
![]() центра инерции или центра тяжести этой
площадки. Следовательно, окончательно
получим
центра инерции или центра тяжести этой
площадки. Следовательно, окончательно
получим
![]() .
(6.10)
.
(6.10)
Так как
![]() ,
то
,
то
![]() .
.
Это означает, что сила давления жидкости на плоскую стенку определяется весом цилиндрического столба этой жидкости с площадью основания, равной площади стенки, и высотой от поверхности до центра тяжести стенки. Если воспользоваться последней формулой, то следует, что главный вектор сил давления на плоскую стенку по величине равен произведению гидростатического давления в центре тяжести стенки на ее площадь.
Точка приложения
главного вектора, называемая центром
давления, в общем случае не совпадающая
с центром тяжести, может быть определена
на основании законов статики твердого
тела. Известно, что момент главного
вектора системы сил равен сумме моментов
составляющих сил, т.е. если обозначим
координаты центра давления
![]() и
и
![]() ,
то уравнения моментов относительно
осей координат будут
,
то уравнения моментов относительно
осей координат будут
![]() ;
;
![]() ;
;
![]() .
.
Из системы этих трех уравнений можно найти три неизвестные величины: и .
Нетрудно
показать, что центр давления расположен
ниже центра тяжести. Если в последнем
соотношении заменим р
по формуле (6.10) и разделим обе части на
![]() ,
то получим
,
то получим
![]() .
.
Как известно,
интеграл, стоящий в правой части,
называется моментом инерции площади
относительно оси Оу.
Если представить соответствующий момент
инерции относительно параллельной этой
оси прямой, проходящей через центр
тяжести, в виде
![]() и вспомнить, что момент инерции
относительно оси, проходящей через
центр инерции, меньше момента инерции
относительно любой другой параллельной
оси, то можно написать неравенство
и вспомнить, что момент инерции
относительно оси, проходящей через
центр инерции, меньше момента инерции
относительно любой другой параллельной
оси, то можно написать неравенство
![]() .
.
Сократив обе части
неравенства на
![]() ,
окончательно получим
,
окончательно получим
![]() .
.
